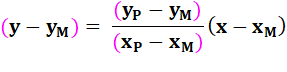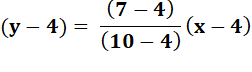|
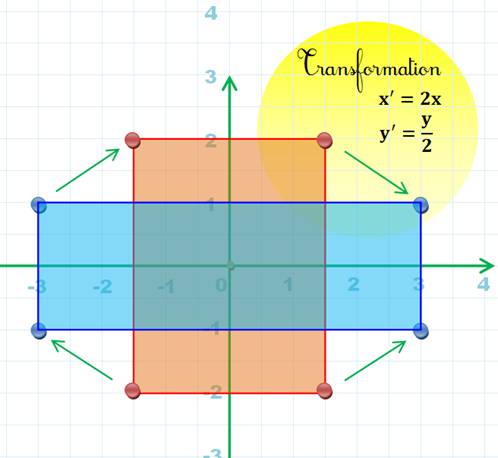
Approche |
|
|
Exemple |
|
|
Pourquoi la nécessité de ces deux
mots ? |
Linéaire
y
est proportionnel à x y
= a . x |
Affine
La
croissance de y est proportionnelle
à celle de x (y1
– y2) = a . (x1 – x2)
|
|
La
fonction affine est une généralisation de la fonction linéaire. Une
fonction affine f fait correspondre à une variable x son produit par un
coefficient a, auquel on ajoute un nombre b
|
||
Ne pas confondre avec:
|
Le complexe
z = a + ib est appelé affixe du point M de
coordonnées (a; b) Le point M est appelé image du complexe z |
|
Définitions |
FONCTION
AFFINE
y est une fonction affine de x Voir équation du premier degré
La fonction qui à un nombre x fait correspondre le nombre ax + b est appelée fonction
affine Fonction
linéaire C'est une
fonction affine particulière pour laquelle b = 0 Fonction
constante C'est une
fonction affine particulière pour laquelle a = 0 ESPACE
AFFINE
L'espace affine euclidien est l'espace
ordinaire de la géométrie L'espace affine est
une forme d'espace plus simple que le précédent, tel qu'il est
tout de même possible d'y émettre des propriétés SUITE
AFFINE
SYSTÈME
AFFINE
|
|
|
|||
|
Voici les trois méthodes expliquées pas à pas. |
|
||
|
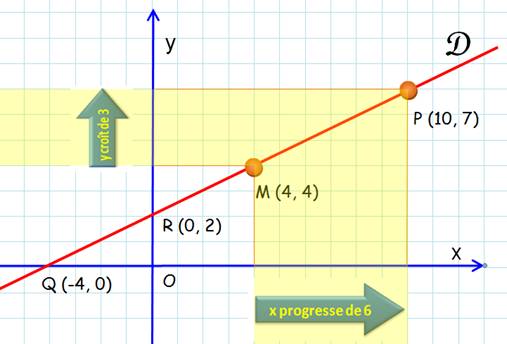
Méthode 1 – avec l'aide d'un graphe
|
y = ax + b |
||
|
|
Si x progresse de 6, je
constate que y progresse de 3. Alors si x progresse de 1, y progressera de ax
= 0,5. Donc a = 0,5 |
||
|
|
Pour x = 0, je lis la
valeur de y sur le graphique: y = b = 2 |
||
|
|
y = 0,5 x + 2 |
||
|
|
0 = 0,5 x + 2 0,5 x = – 2 x = – 2 / 0,5 x = – 4 Ce qui est bien la valeur
lue sur le graphe. |
||
|
Méthode 2 – analytique (sans graphe)
|
y = ax + b |
||
|
|
M P |
||
|
|
4 = 4a + b 7 = 10a + b 3 =
6a |
||
|
|
a = 3/6 = 0,5 |
||
|
|
4 = 4 x 0,5 + b b = 4 – 2 = 2 |
||
|
Méthode 3 – algébrique ou directe
|
|
||
|
|
|
||
|
|
y – 4 = y = 0,5 x – 0,5 x 4 + 4 y = 0,5 x + 2 |
||
Voir Équation cartésienne de la
droite et exemples
![]()
|
Exemple |
La fonction qui,
à x heures, fait correspondre le prix total est notée: Ce type de
fonction est une fonction affine |
|
Origine |
Regiones
adfines barbaris: les
régions voisines des barbares Tuus
adfinis: ton parent par alliance |
![]()
|
Anglais |
Linear function In real analysis, a linear function is a function f such that Linear equation A linear equation in one variable x is an equation of the form Linearly dependent A set of vectors u1 , u2
… un is linearly independent if Otherwise, the set is linearly dependent |
|
En savoir plus |
|
![]()
![]()
|
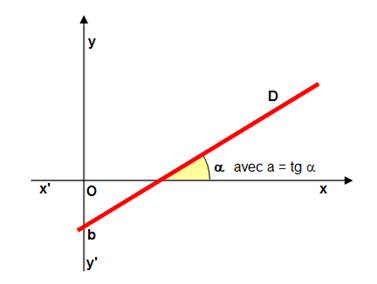
Définition mathématique & Représentation |
FONCTION
AFFINE ou APPLICATION AFFINE
la représentation
graphique d'une fonction affine est une droite passant par le point de coordonnées (0,
b) et de coefficient directeur a. a
est égal à la tangente de l'angle de la droite avec l'axe des x, b est
appelé l'ordonnée à l'origine.
Si le coefficient
b est nul, la relation y = a.x
définit une relation linéaire. Alors a
est un simple coefficient de proportionnalité La relation
classique de la vitesse est une relation linéaire: d = v.t (distance parcourue égale vitesse
par temps).
Lorsque b
n'est pas nul, ce sont les accroissements de y qui sont proportionnels aux accroissements de x. Ainsi vu, on peut
conclure que a est le coefficient de proportionnalité. |
|
Généralisation |
dans l'espace
affine F,
attaché à l'espace vectoriel F0 ,
s'il existe une
application linéaire L de E0 dans F0 et un point a
de E tels que f(x + a) = L(x) + f(a)
pour tout x de
E0 L
est dite la partie
linéaire de f. |
![]()
|
ESPACE
AFFINE
les notions
d'orthogonalité (angle droit), de distance ou de produit scalaire sont
importantes. Cercle et ellipse
sont deux objets distincts. C'est la
géométrie classique que nous apprenons en classe.
ces notions ne
sont pas utiles. Cercle et ellipse
sont deux objets qui ne sont pas distingués. C'est une
généralisation de la géométrie.
On dit:
rechercher les invariants du groupe.
Un espace "tout
nu" n'a pas d'origine privilégiée. Il faut choisir
une origine pour définir un espace vectoriel (un espace dans lequel on peut
se repérer). Alors, en
choisissant un vecteur d'extrémités
données (un bipoint), il est possible de structurer cet espace: utilisation
de la notion d'opérateur de translation. C'est la notion d'espace affine. PLAN
AFFINE
Un élément (x, y)
de R² est représenté par un point
M, ou un vecteur OM. Lorsque les
éléments de R² sont considérés comme des points, on dit que R² est muni de la
structure affine.
|
![]()