Conjecture des lits superposés

Édition du: 10/12/2024

INDEX Graphe Topologie Géométrie Logique Dénombrement Jeux	GRAPHES, ARBRES & RÉSEAUX
	Graphes – Index et vocabulaire		Graphe simple
	Graphes – Introduction	Arbres – Introduction	Graphe planaire
	Nœuds	Croisements	Graphe eulérien
	Nombres de Ramsey	Graphes superposés	Tournoi

Faites un double-clic pour un retour en haut de page

Conjecture des lits superposés

On devrait dire: conjecture des graphes superposés. Où il est question de la duplication d'un graphe et de la réunion du couple par des arcs évanescents. Le problème consiste à comparer des chemins dans le graphe et à déterminer la probabilité des plus fréquents.

Applications en physique de la percolation: écoulement de fluides à travers des matières granulaires.

Sommaire de cette page

>>> Approche – Graphes superposés

>>> Chemins vers la conjecture

>>> Conjecture des lits superposés

>>> Avancée récente: conjecture fausse

>>> Des hypergraphes aux graphes

Débutants

Dénombrement

Glossaire

Combinatoire

Anglais : Bunk bed conjecture or bunkbed conjecture (bunkbed = lit superposé)

Analogie

Mon bureau est au rez-de-chaussée et mon meilleur collègue se trouve à l'autre bout du bâtiment. Notre boss est au premier étage tout juste au-dessus de lui.

La conjecture dit que je trouverai plus probablement le chemin pour aller voir mon collègue que le chemin vers mon boss, surtout si certains escaliers sont parfois condamnés.

Approche – Graphes superposés		haut
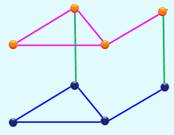
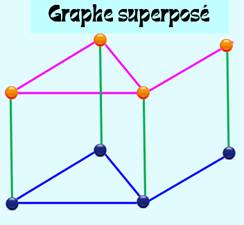
Construction du graphe superposé Un graphe superposé, ou lits superposés, est constitué: d'un graphe du bas (bleu), dit couchette du bas; d'un graphe du haut (mauve) identique (isomorphe), dit couchette du haut; et d'arêtes (vertes) reliant les sommets homologues, dits piliers. Selon la quantité de piliers, on compare le chemin menant du point A au point B dans l'étage du bas et le chemin menant du point A au point B', homologue de B mais à l'étage du haut.	Graphe typique Cette figure fait penser à une configuration de lits superposés.
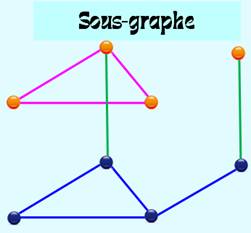
Sous graphes Le graphe formé de toutes les arêtes et un graphe complet. En supprimant telle ou telle arêtes, il est possible de former une grande quantité de sous-graphes. Applications Pourquoi un tel "amusement" ? Il s'agit de créer un outil d'étude des phénomènes de percolation: passage de fluide dans des matériaux poreux ou des matières granulaires, écoulement de l'eau à travers une éponge, pénétration lente des eaux de pluies dans le sol, etc. Ce sont des phénomènes évolutifs et, avec leur modélisation en graphes, cette dynamique se traduit par la disparition de certaines arêtes. D'où la formation de sous-graphes.	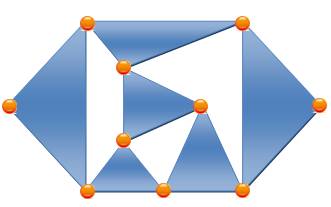Sous-graphe typique

Chemins vers la conjecture

haut

Chemin du bas et chemin vers l'étage

Selon le sous-graphe considéré, il existe quatre possibilités:

aucun chemin en bas comme vers le haut;

un chemin en bas et pas vers le haut;

pas de chemin en bas et un vers le haut; et

un chemin en bas comme un chemin vers le haut.

Probabilité de chemins

On compare la probabilité d'existence des chemins dans les sous-graphes.

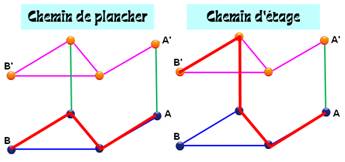
Comparaison des chemins

Selon la conjecture, le chemin de gauche est plus fréquente que celle de droite.

Conjecture

Fausse ?

La probabilité d'un chemin de plancher est plus grande ou égale à la probabilité d'un chemin vers l'étage.

La probabilité

que A de la couchette du bas soit connecté à B de la couchette du bas

est plus grande ou égale que

La probabilité

que A soit connecté à B', la copie correspondante de B dans la couchette supérieure.

Pendant quatre décennies, la conjecture du lit superposé est restée une idée acceptée et apparemment évidente dans le domaine des graphes aléatoires, sans que quiconque n’en remette en question la validité.

En novembre 2024, cette conjecture fut infirmée par la découverte d'un cas où la probabilité était plus petite. Cas exceptionnel, mais suffisant pour annihiler cette affirmation.

Conjecture des lits superposés

Général

Domaine de la théorie de la percolation, branche des mathématiques qui étudie le comportement des clusters connectés dans un graphe aléatoire.

1985 – Pieter Kasteleyn (néerlandais) propose cette conjecture.

2024 – Nikita Gladkov, Igor Pak et Alexander Zimin trouvent un contre-exemple.
Igor Pak est professeur à l’université de Californie à Los Angeles (UCLA),
Leur publication reste encore a être soumise à l'évaluation par les pairs.

Plus précisément: choix des sous-graphes

Une probabilité est attribuée à chaque arête du graphe. Les arêtes de la couchette supérieure et leurs arêtes correspondantes de la couchette inférieure partagent la même probabilité. Les probabilités attribuées aux poteaux peuvent être arbitraires.

Un sous-graphe aléatoire du graphe à couchettes est ensuite formé en supprimant indépendamment chaque arête en fonction de la probabilité attribuée.

Avancée récente: conjecture fausse		haut
Trois collègues Igor Pak doutait de la véracité de la conjecture. Il développe un programme de recherche exhaustive pour dénicher un contre-exemple. Il demande la coopération de Nikita Gladkov et Alexander Zimin. Ces derniers avaient testé les cas jusqu'à neuf arêtes et n'avaient pas trouvé de cas contraire à la conjecture. Trop long et sans résultat	La nouvelle méthode L’équipe décide d'utiliser l’apprentissage automatique (machine leraning). Elle a entraîné un réseau neuronal à produire des graphiques avec des chemins sinueux qui pourraient potentiellement privilégier le saut vers le haut. Ils découvrent certains chemins vers le bas était à peine plus probable que leurs alternatives vers le haut. Mais le modèle n’a découvert aucun graphique où l’inverse était vrai. Donc, pas de résultat.
Doutes Les trois amis font face à des volumes de calculs rédhibitoires. Ils doutent que l'une ou l'autre méthode conduira à une conclusion. après sept ans de labeur, ils lâchent l'affaire out en la gardant dans leurs préoccupations.	Hypergraphes C'est une avancée concernant les hypergraphes qui va relancer les recherches. En juin 2024, Lawrence Hollom (Cambrige), trouve un cas d'exception à la conjecture, mais en hypergraphe d'ordre 3.

Des hypergraphes aux graphes

haut

Hypergraphe d'ordre 3

Ce sont des graphes dont les arêtes ne sont plus de lignes, mais des triangles.

Dans ce, cas ce sont trois sommets qui sont reliés entre eux.

En juin 2024, Lawrence Hollom crée ce 3-hypergraphe qui est un contre-exemple de la conjecture dans ce monde des hypergraphes.

Nikita Gladkov, Igor Pak et Alexander Zimin en profite pour tenter de projeter cette solution dans le monde des graphes.

Pour cela, chaque liaison triangulaire est remplacée par 1 202 liaisons simples (arêtes). Soit un graphe géant de 7 222 sommets et 14 422 arêtes.

Et c'est un succès: un contre exemple de la conjecture des lits superposés.

Contre exemple avec un 3-hypergraphe

Note: 7 222 = 10 + 6 × 1 202 sommets

Haut de page

Retour	Graphe planaire Percolation et programmation amusante
Suite	Arbres à dénombrement avec nombres de Catalan Arbres de distribution Chemin le plus court Vocabulaire des graphes Coloration des graphes (nombre chromatique) Graphes et problèmes NP Petit monde Sept amis autour d'une table
Voir	Code Gray Croissance logistique Énigmes et paradoxes Graphe de Delaunay Intelligence artificielle Jeux – Index Logique formelle Percolation Relier les points d'un seul coup de crayon Topologie – Glossaire Tour de Brahmâ Trois maisons (énigme des -)
Sites	La « conjecture du lit superposé » en mathématiques a été réfutée après près de 40 ans – Éric Rafidiarimanana – DailyGeekShow Bunkbed conjecture – Wikipedia The bunkbed conjecture is not robust to generalization – Lawrence Hollom The bunkbed conjecture is false – Nikita Gladkov, Igor Pak et Alexander Zimin The Bunkbed conjecture was just debunked ! – Dr. Trefor Bazett – Vidéo en anglais The bunkbed conjecture is false – Igor Pak's blog
Cette page	http://villemin.gerard.free.fr/aMaths/Topologi/aaaGraph/LitSuper.htm