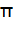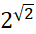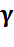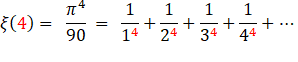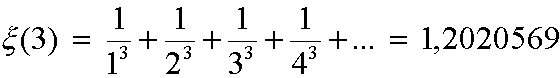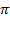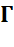NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 06/04/2022 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	NOMBRES
Débutants Types de Nombres	TYPES				Glossaire Nombres
INDEX Types de nombres	Entiers	Rationnels	Algébriques	Décimaux
	Relatifs	Irrationnels	Transcendants	Réels
	Normaux	Gauss	Idéaux	Complexes
	Bref aperçu		Infinitésimaux	Transfinis
		Sommaire de cette page >>> Approche >>> Historique >>> Propriétés >>> Quelques nombres transcendants >>> Exemples particuliers

Les nombres algébriques sont comme les étoiles sur le fond du ciel, et l'obscurité épaisse est le firmament des nombres complexes.

M. Boll – Cité par A. Moatti

Voir Pensées & humour

NOMBRES TRANSCENDANTS

Certains nombres irrationnels ne peuvent pas s'exprimer par une relation simple (équation à coefficients entiers, par exemple).

Ce sont les nombres transcendants (comme ).

C'est Joseph Liouville qui prouva leur existence.

Les nombres transcendants sont des nombres irrationnels qui ne sont pas algébriques

Autrement dit: ni exprimables par une fraction (ratio) ni par une équation

Les décimales sont en nombre infini et elles sont totalement imprévisibles.

Quelques transcendants

Nombres construits 0, 1101001000100001…. 0, 12345678910111213… 0, 248163264128256…

Constantes classiques est le plus connu de tous >>> e est un autre exemple >>>

Anglais: transcendental numbers

APPROCHE
Nombre transcendant de Liouville 0,11 000 1 00000 000000000000 1 000000000.... = 10^-1! + 10^-2! + 10^-3! + 10^-4! +... Les "1" se trouvent en position 1, 2, 6, 24, 120 … = k! Soit, une multiplication de chacune par 2, 3, 4, 5 … Suite >>>

HISTORIQUE

C'est seulement au XVII^e siècle que l'on commence à faire la distinction entre les nombres algébriques, racine de polynômes à coefficients entiers, et les autres réels qui sont qualifiés de transcendants. Leur existence n'a été prouvée qu'au XIX^e siècle. Liouville démontra en 1844 l'existence de nombres transcendants et en construisit plusieurs, dont celui-ci, le plus simple. C'est le premier exemple historique de nombre transcendant. Cantor en 1873, déduit l'existence des nombres transcendants de son théorème prouvant que l'ensemble de tous les nombres réels est non dénombrable. Ce qui veut dire qu'un nombre pris au hasard (en se donnant, par exemple, son développement décimal illimité) n'a aucune chance d'être algébrique. Après Charles Hermite (1873) et Ferdinand von Lindemann (1882), démontrant que e et sont transcendants. Il faut attendre 1929 pour de nouveaux résultats dans le domaine de la transcendance. Hermite démontre la transcendance de e. Il pense que pour , il faudra déployer de gros efforts. Lindemann réussit  l'exploit, 9 ans plus tard. Il utilise la même méthode qu'Hermine, en s'appuyant sur la formule d'Euler.

Propriétés

Les transcendants s'écrivent sous la forme de décimales infinies et non répétitives. Tous les nombres transcendants sont irrationnels. La plupart des irrationnels sont transcendants. Alors que l'ensemble des nombres algébriques est dénombrable, celui des nombres transcendants (expressions équivalentes): est largement "plus grand", est indénombrable, a la puissance du continu, a un cardinal transfini. Théorème de Hermite-Lindemann Pour tout nombre algébrique a, e^a est transcendant. Voir Constante de Ramanujan avec 163 Théorème de Gelfond - Schneider Si a est un nombre algébrique distinct de 0 et de 1, et si b est algébrique irrationnel (Cad : n'est pas rationnel), alors a^b est transcendant. Voir Principe des tiroirs Exemple est donc transcendant Voir ce nombre / R2^R2 Excellent moyen pour créer des nombres transcendantaux. Résout le septième problème de Hilbert. Corollaire: si b est un nombre algébrique dans C avec i.b non dans Q, alors exp(Pi .b) est transcendant. Généralisation: Théorème de Baker (1966-67) e^a . n^b . m^c …. est transcendant a, b, c … n, m … nombres algébriques non nuls. ln (a) est transcendant a, algébrique positif supérieur à 1. Forme linéaire de logarithmes de nombres algébriques Le théorème de Baker permet de montrer, par exemple, que les nombres suivants sont transcendants pour tous nombres algébriques x, y et z: x . log(2) + y . log(3) + z . log(5) Les fonctions trigonométriques comme sinus ou cosinus sont des fonctions transcendantales

Quelques nombres TRANSCENDANTS
, e , ln 2 …	Sont des nombres TRANSCENDANTS

ln 2 = 0, 693 147 …	Constante de Mercator ou de Grégory. ln 2 = log 2 en base e = 1 - 1/2 + 1/3 - 1/4 + ... La série harmonique alternée. Voir Valeur de ln 2 / DicoNombre
G = 0,8346268…	Constante de Gauss. Moyenne arithmético-géométrique de 1 et de la √2. Voir Valeur G / DicoNombre
e = 2, 718 281 …	Transcendance démontrée en 1872 par C. Hermite. Méthode reposant sur des approximations de la fonction e^z par des fonctions rationnelles. Premier nombre, non construit pour la circonstance, à être reconnu comme transcendant. Voir Constante e / DicoNombre
= 3, 141 592 …	Transcendance démontrée en 1882 par Lindemann par généralisation de la méthode de Hermite. Prouve définitivement l'impossibilité de la quadrature du cercle. Voir Constante Pi / DicoNombre
e . = 8, 539 734 22 ... e + = 5, 859 874 482 ...	L'un des deux est transcendant, peut-être les deux. Voir Nombres e et Pi / DicoNombre 5,8 / DicoNombre 8,5
= 23,140 … = 22,459 …	Le premier est transcendant. On ignore si le deuxième l'est; on ne sait pas non plus s'il est irrationnel. Voir Nombres e et Pi / DicoNombre 22,4 / DicoNombre 23,1
= 23, 140 …	Sa transcendance ne fut démontrée qu'en 1930, suite à la question de Hilbert posée en 1900. Ce nombre n'est pas solution d'une équation à coefficients entiers. Il s'écrit avec une suite infinie de décimales non répétitives. Voir DicoNombre
= 0,207 879 576...	Si a est algébrique et si b est algébrique irrationnel, alors a^b est transcendant. Or i est algébrique et irrationnel, le théorème s'applique: i^i est transcendant. Voir Puissance de l'imaginaire / DicoNombre

= 2, 665

Nombre de Hilbert transcendant. Démonstration en 1930. Aussi un des problèmes de Hilbert Théorème de Gelfond - Schneider: a algébrique et b irrationnel => a^b transcendant De nombreuses fonctions trigonométriques ou hyperboliques de nombres algébriques non - nuls sont transcendantes. Voir DicoNombre

0,11000100...	Nombre de Liouville (1844): transcendant. = 10^-1! + 10^-2! +10^-3! +... = 0,110001000000000000000001000 ... Les 1 se trouvent en : 1, 2, 6, 24, etc. Voir Liouville
0,01101001 ...	Nombre de Morse-Thue: transcendant. Voir Morse-Thue
0,123456789	Nombre de Champernowne ou de Mahler Suite concaténée des nombres (1933): transcendant. = 0,1234567891011121314151617181920 ... Ce nombre est normal, mais pas de Liouville.

= 0,577... = 1,781 = 0,561	Constante d'Euler (gamma). Sans doute transcendant, mais non prouvé. On ne sait même pas si elle est irrationnelle. = lim n® ¥ (1 + 1/2 + 1/3 + 1/4 + ... + 1/n - ln(n)) = 0,577 215 664 901 532 860 606 512 090 082 402 431... Si, un jour, on trouvera une fraction rationnelle (gamma = a/b) , alors b est supérieur à 10^10000. Voir constante d’Euler / DicoNombre
G = 0, 915...	Constante de Catalan. Sans doute transcendant, mais non prouvé. G = S (-1)^k / (2k + 1 )² = 1/1² - 1/3² + 1/5² - 1/7² + ... = 1 - 1/9 + 1/25 - 1/49 + ... Voir Constante de Catalan / DicoNombre

(n)	Fonction zêta. Certaines valeurs de la fonction zêta sont transcendantes, comme (3). Avec les fonctions transcendantes, il peut exister des points rationnels ayant des valeurs transcendantes.
= 1,202 056 9 …	zêta (3) Constante d’Apéry. Limite de la fonction de Riemann d'ordre 3 Irrationnel sûr, mais transcendant? Connu en 1998 avec 32 000 279 décimales. Sebastian Wedeniwski. 35 heures de calcul. Voir ce DicoNombre
= 1,082 323 237 ...	zêta (4) Transcendant. On sait depuis Euler que toutes les suites en 2k s'expriment en ^2k, valeurs transcendantes. Voir DicoNombre
(n) (1/3) = 2,678 938 534 7...	Factorielle généralisée. (1/3) transcendant et indépendant de . (1/4) transcendant. (1/5) on ne sait pas. (n) = factorielle généralisée. Indépendance algébrique: il n'existe pas de polynôme à coefficients non nuls liant ces deux nombres et prenant la valeur nulle. Les nombres , , et (1/4) sont indépendants (démonstration 1995). Voir DicoNombre

2,502 ... 4,669 ...	Nombres de Feigenbaum (1975). Sans doute transcendant, mais non prouvé. Valeur d'étirement des figures fractales. Facteur d'échelle de transformation des figures fractales. Dédoublement de période dans les systèmes chaotiques. Ces deux valeurs sont universelles, comme . Voir DicoNombre 2, 52 / DicoNombre 4, 669
C = ? ? ?	Constante de Chaitin. Probabilité pour qu'un algorithme aléatoire s'arrête. Noam Elkies d'Harvard note que ce nombre transcendantal est, en prime, non calculable.

En 1975, Martin Garner a fait croire que ce nombre est un entier. Non seulement il ne l'est pas, mais il est transcendant.  Voir Autres nombres du même style

Voir Liste d'irrationnels

Suite	Nombres réels Types de nombres – Index Mot infini de Fibonacci Nombre - Glossaire
Voir	Calcul mental – Index Carré magique débutant Décimalisation Ensemble - Glossaire Équations Fraction - Glossaire Géométrie Groupes Lambert Liouville Nombre et anglais Nombre imaginaires Nombres périodiques Riemann Rubriques débutants Théorie des nombres Types de nombres selon leurs diviseurs
Nombres	Liste des nombre de 0 à l'infini et de leurs propriétés Un Constante e Constante Pi Constantes Infini Racine de deux Zéro Zêta
Livre	Les indispensables mathématiques et physiques pour tous – Alexandre Moatti – Odile Jacob – 2006. Pour tous ceux qui veulent compléter leurs connaissances sur ce sujet et bien d'autres. Très abordable.
Sites	Théorème de Baker – Wikipédia Linear forms in logarithms – Jan-Hendrik Evertse – 2011
Cette page	http://villemin.gerard.free.fr/Wwwgvmm/Type/Transcen.htm