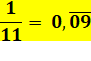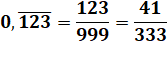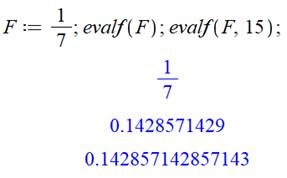|
|||||||||||||||||||||||||||||||||||||||||||||
![]()
|
NOMBRES PÉRIODIQUES Tour
d'horizon |
|
|
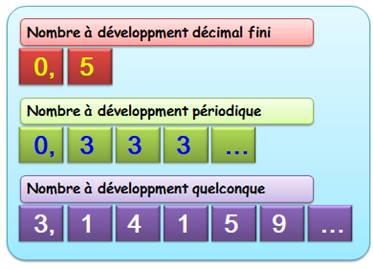
Trois
types de nombres réels selon le
comportement des chiffres après la virgule:
Les
nombres à développement fini peuvent être assimilés aux nombres périodiques
en les complétant avec des zéros à droite. Ex: 0,5 =
0,5000… et aussi: 5 = 5,000… |
Nombre
périodique Nombre qui à partir
d'un certain rang présente un groupe de chiffres qui se répètent sans fin.
Comme 09 dans 1/11 = 0,090909… On note:
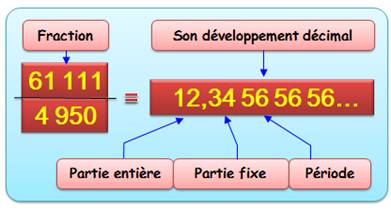
12,34 est
la partie fixe et 0,34 est la partie fixe non entière. |
Voir Nombres réels
Nombres périodiques sous diverses formes

Notez: Le passage de la fraction
à la notation décimale n'est jamais qu'une division.
|
|
||
|
Prenons le nombre donné en exemple. C'est
une fraction qui peut être développée en un nombre
rationnel selon notre système
décimal. |
|
|
Note: nombres à virgule
= nombres décimaux
|
|
||
|
Un nombre
est périodique si dans sa partie décimale un motif se répète indéfiniment. La partie
répétitive est la période qui peut être précédée d'une partie fixe. |
Un nombre périodique classique: 1/3 = 0,333… Un peu plus sophistiqué: 1/7 = 0,142857142857… Un nombre périodique banal: 1/2 = 0,5000… En fait, dans ce dernier cas, le chiffre 0 est
bien répété, mais il est inutile. On distingue de tels nombres en tant que
nombres décimaux. |
|
Anglais: a recurring decimal is a decimal number that has
digits that repeat forever
|
|
||
|
Le nom de
nombres
décimaux est réservé aux nombres totalement connus; aux nombres ayant une
quantité finie de décimales. Note: Ils sont parfois inclus dans la définition des
nombres périodiques avec une période égale à 0. Un nombre réel est un nombre décimal si et seulement si son
développement décimal n'est constitué que de zéros à partir d'un certain
rang. |
Propriété Ce sont les nombres issus d'une fraction ayant
pour dénominateur un nombre d = 2a. 5b. Quelques nombres décimaux: 0,5
/ 0,25 / 0,2 / 0,125 / 0,1 / 0,0625 / 0,05 / 0,04 / 0,03125 / 0,025 / 0,02 /
0,0125 / 0,01 / 0,008 / 0,00625 / 0,005 … En représentation Un nombre décimal possède plusieurs
représentations: 0,5 = 0, 5000… = 0,4999… On peut toujours remplacer les 0 terminaux par
des 9, tout en décrémentant d'une unité le dernier chiffre significatif. |
|
Suite en Développements finis
|
|
||
|
Les
nombres périodiques, y compris les nombres décimaux, sont des nombres
rationnels: ils peuvent s'exprimer sous la forme de fractions. Un nombre réel est
rationnel si et seulement si son développement décimal est périodique ou
fini. |
Transformation d'un nombre
rationnel en fraction N
= 0,123123123123… 1000 N = 123,123123123123… 999N =
123
|
|
|
Tout
nombre rationnel est soit un nombre décimal ou un nombre périodique. Les
nombres décimaux et les nombres périodiques sont rationnels. Every rational number is
either a terminating or repeating decimal. Every repeating or
terminating decimal is a rational number. |
||
|
Il existe
des nombres dont on ne connaitra jamais toutes les décimales. Ce sont les nombres
irrationnels. |
Quelques nombres irrationnels
|
|
|
Nombre
rationnel est représenté par une fraction Le
logiciel Maple transforme
une fraction en nombre rationnel avec l'instruction evalf. Exemple de programmation avec Maple |
|
|
|
Soit la fraction:
12/33. Le logiciel la simplifie automatiquement en 4/11. L'instruction evalf
donne le développement décimal avec 10 chiffres. Soit: 0.3636… Le logiciel offre la
possibilité de travailler sur la période avec le groupe (package) de
logiciel: numtheory. L'instruction
pdexpand fournit à la suite:
Avec L, on calcule la
longueur de la période en extrayant (op) le quatrième élément de FF et en
comptant la quantité de chiffres (nops). |
|
|
Attention à la
précision demandée. - evalf(F) produit
10 chiffres; et - evalf(F,15) produit 15 chiffres. Notez comment le
logiciel arrondi le dernier chiffre. |
Voir Programmation – Index
|
|
|
|
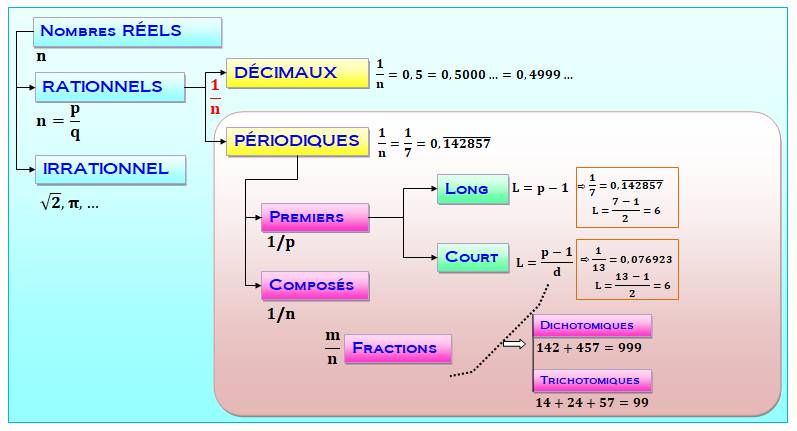
De réels à périodiques Parmi
tous les nombres (nombres réels),
certains peuvent s'exprimer sous la forme de fractions
(nombres rationnels)
et c'est impossible pour d'autres (nombres irrationnels)
comme racine de 2 ou Pi. Parmi les
nombres rationnels (p/q ou q/p), certains ont un développement décimal
comportant une quantité de décimales (chiffres derrière la virgule) finie,
comme ½ = 0,5. Ce sont les nombres décimaux. De
tels nombres peuvent être prolongés avec des 0. Ceux-ci sont totalement
inutiles sauf à englober ces nombres dans l'ensemble des nombres périodiques. Les nombres périodiques sont formés à partir d'un
certain rang de blocs de chiffres qui se répètent sans fin. Illustration
Structure des nombres périodiques Un nombre
périodique est défini par quatre paramètres: signe,
partie entière, partie décimale fixe et partie décimale répétitive, dite
période. La période est caractérisée par sa longueur (L).
Avec les nombres premiers
(p), le développement décimal de 1/p produit une période dont la longueur maximale est L = p – 1 (premiers
longs) ou une fraction de cette valeur ((p – 1) / d. Avec ces
fractions, on s'intéresse alors à deux propriétés:
|
|
Voir Classification
des nombres – Ensembles
|
Conversions ou recherches |
||||
|
De |
Vers / en |
Méthode |
Programme |
|
|
Nombres décimaux |
Fractions |
|
||
|
Fractions |
Nombres à décimales |
|
||
|
Nombres périodiques |
Fractions |
|
||
|
Fractions |
Nombres périodiques |
|||
|
Fractions |
Premiers longs ? |
|||
|
Nombres
réels |
Extraction des décimales |
|||
|
Nombres
réels |
Base b |
|||
|
|
||
|
Notation décimale |
Notre
manière habituelle d'écriture les nombres avec ou sans une virgule. Comme:
12,34 ou 0,333… |
|
|
Développement décimal |
Expression
d'une fraction sous la forme d'un nombre. Comme ½ = 0,5 ou 1/7 =
0,142857142857… |
|
|
Décimales |
Les
chiffres derrière la virgule. C'est 3, 4 et 5 pour 12,345. |
|
|
Séparateur décimal |
Le symbole
qui sépare la partie entière de la partie décimale. C'est la virgule pour
nous et le point pour les Anglo-Saxons et pour les calculatrices. |
|
|
Nombres décimaux |
Nombres
dont le développement décimal est limité. Note: a decimal fraction is a
fraction the denominator of which is a power of ten. |
|
|
Nombre à virgule |
En
principe, exact synonyme de nombre décimal. Parfois utilisé pour désigner un
nombre réel comportant des décimales. |
|
|
Nombre périodique |
Un nombre
dont les décimales, à partir d'un certain point, sont des paquets de chiffres
répétitifs. Comme 1,666… ou 0,111… |
|
|
Partie fixe |
Dans un
nombre périodique, la partie fixe qui précède la partie répétitive. Ex: 12
dans 0,12666… |
|
|
Partie entière |
Le nombre
à gauche de la virgule. C'est 12 pour 12,345. |
|
|
Partie décimale |
Le nombre
à droite de la virgule. C'est 345 pour 12,345 |
|
|
Zéro finaux |
Désigne les
zéros prolongeant un nombre décimal. Ex: 0,50000. Ces zéros sont généralement
inutiles (en science, ils peuvent témoigner de la
précision attribuée à la valeur). |
|
|
Nombre périodique simple Nombre périodique mixte |
Simple: la
période commence immédiatement derrière la virgule. Mixte:
elle comporte une partie initiale non périodique. |
|
|
Période |
Partie
répétitive d'un nombre périodique. C'est 09 dans 0,090909… Parfois
utilisé pour désigner la longueur de la partie périodique. |
|
|
Période longue ou maximale |
Longueur
de période égale au dénominateur moins un. |
|
|
Dichotomie Trichotomie |
Pour un
nombre périodique de longueur de période paire, le fait de couper la période en
deux moitiés ou trois tiers. |
|
Voir DicoMot Math
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Aussi |
|
|
Sites |
|
|
Cette page |
http://villemin.gerard.free.fr/Wwwgvmm/Nombre/aaaCycli/NbCycHor.htm |
![]()