|
|||||||||||||||||||||||||||||||||||||||||||||
![]()
|
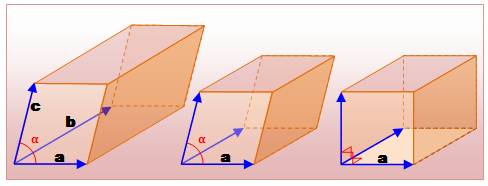
Rhomboèdre ou hexaèdre rhombique Le rhomboèdre est un parallélépipède
particulier; ses faces sont des losanges
(rhombus). Le cube est
un rhomboèdre particulier: faces carrées.
Parallélépipède Rhomboèdre Cube Le rhomboèdre peut être régulier
ou non; aigu ou obtus. Le rhomboèdre, comme le parallélépipède, fait
partie de la famille des prismes. |
Cristal de calcite dont la maille est rhomboédrique de taille 5 Anströms.
C'est bien rhombOèdre et non rhombaèdre! |
Anglais: Rhombohedron
|
|
|||
|
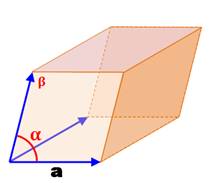
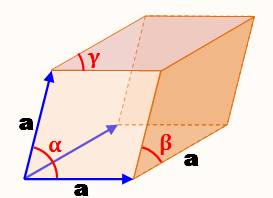
Définition Le
rhomboèdre est une sorte de cube
"penché", sans ses angles droits. Le
rhomboèdre est un parallélépipède dont les six faces sont des losanges
identiques ou non, mais … toutes les arêtes ont
même longueur (le premier losange dessiné impose la longueur des côtés
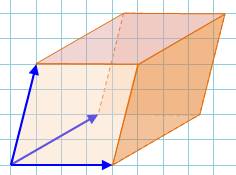
pour les autres). Les trois
vecteurs
directeurs (bleus) ont la même norme (longueur), leur direction est
quelconque. |
Rhomboèdre: six faces en losanges
Toutes les faces sont des losanges (identiques ou non) dont les côtés
sont tous de même longueur; par contre, les angles peuvent être différents. |
||
|
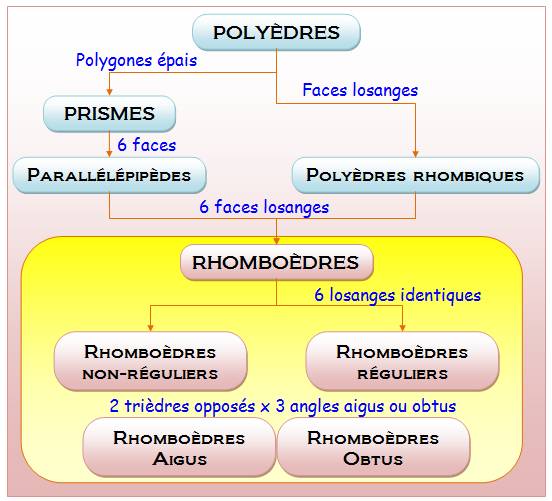
Famille Le rhomboèdre appartient la famille des prismes,
volume qui "donne une épaisseur" au polygone, en l'occurrence au
losange. Un rhomboèdre est un polyèdre rhombique,
familles des polyèdres à 6, 12 ou 30 faces losanges:
Aucune autre possibilité. |
|
||
Voir Famille des
parallélépipèdes (ou pavés)
|
|
||
|
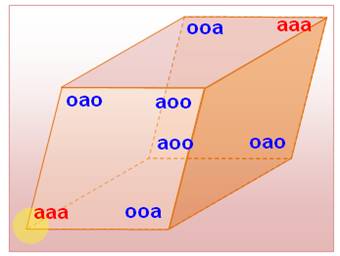
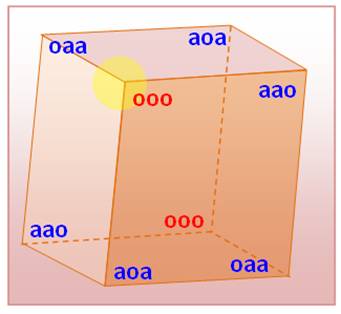
Configuration des angles Trois
angles à chaque sommet (trièdre) et six sommets font 24 angles, dont 12 en
angles aigus alpha (a) et 12 en angles obtus bêta (b). Les trièdres
des sommets opposés sont de même nature. Il existe
deux types de rhomboèdres selon que deux trièdres opposés sont à angles aigus
ou à angles obtus. Rhomboèdre AIGUS "Cube étiré par deux sommets opposés" Deux
trièdres en "aaa", tous aigus; aucun (normal!)
en "bbb", qui seraient tous obtus. Les
autres sont à: un aigu et deux obtus. Pour ce
type de rhomboèdre, la valeur maximale du trièdre est atteinte pour le cube
avec 3 x 90° = 270°. Rhomboèdre OBTUS "Cube compressé par deux sommets
opposés" Deux
trièdres en "bbb", tous obtus. Les
autres sont à: un obtus et deux aigus |
Avant/arrière,
haut/bas, gauche/droite
|
|
|
|
|||
|
Le rhomboèdre régulier est composé de six losanges
identiques (congruents). Le
rhomboèdre régulier est défini par la longueur de ses arêtes (a) et par
l'angle d'inclinaison (alpha). L'angle bêta est son supplémentaire
(la somme des deux angles vaut 180°). Les trois angles au départ des vecteurs
bleus valent alpha. |
Le rhomboèdre régulier, comme le losange, est simplement définit par une longueur et un angle. |
||
|
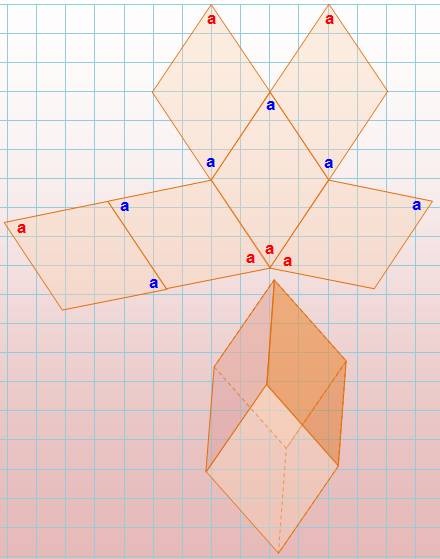
Développement du rhomboèdre
régulier (patron) Mise en
évidence des six faces et des 24 angles, autant en alpha qu'en bêta. Les
angles alpha (ici aigus) sont notés a, et a pour les deux
sommets opposés dont les trièdres sont en aaa. Ce
repérage permet de placer les faces dans le bon ordre. |
|
||
|
|
||
|
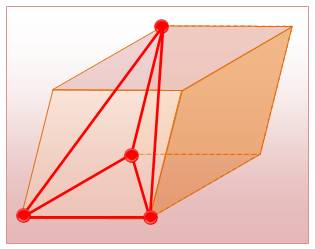
En
choisissant deux pairs de sommets sur des arêtes non-adjacentes, on forme un tétraèdre
orthocentrique ou orthogonal: les paires d'arêtes opposées sont orthogonales. Les
hauteurs du tétraèdre sont concourantes d'où le nom d'orthocentrique. Un
tétraèdre est orthocentrique si et seulement si il est inscrit dans un
rhomboèdre. |
Tétraèdre défini dans le rhomboèdre |
|
![]()
|
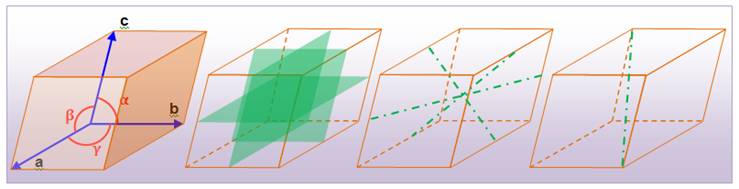
Système rhomboédrique Un cristal fait parie
de ce système s'il possède un axe de symétrie d'ordre 3 (ternaire). Il a trois axes
d'ordre 2, de longueur égale et formant des angles de 120° dans le même plan.
Le quatrième axe, normal à ce plan est soit plus long ou plus court. Il a trois plans de
symétrie et un centre de symétrie. Plusieurs formes
cristallines sous ce système: rhomboèdre, trapézoèdre, scalénoèdre
ou pyramide trigonale. Exemples:
quartz, tourmaline, corindon, calcite. Le
quartz à basse température cristallise dans un système rhomboédrique et, à
haute température, en un système hexagonal. Dans le cas du rhomboèdre:
Maille
élémentaire / 3 plans de symétrie /
3 axes d'ordre 2 / 1 axe d'ordre 3
Système orthorhombique Un
cristal fait partie de ce système s'il a au moins deux axes d'ordre 2 ou deux
plans de symétrie, aucun axe de rotation d'ordre supérieur ne doit être
présent. |
Voir Cristallographie
|
|
||
|
A rhombohedron is a parallelepiped bounded
by six rhombi such that opposite faces are
congruent. |
A rhombohedron
having all six rhombic faces congruent is known as a trigonal trapezohedron. Special cases include the cube and
two golden rhombohedra. The silver rhombohedron (a.k.a the trigonal trapezohedron) is a
three-dimensional object with six faces composed of congruent rhombi. |
|
![]()
|
Suite |
|
|
Aussi |
|
|
Site |
|
|
Cette page |
![]()