NOMBRES - Curiosités, théorie et usages

 

Accueil                           DicoNombre            Rubriques           Nouveautés      Édition du: 26/12/2020

Orientation générale        DicoMot Math          Atlas                   Actualités                       M'écrire

Barre de recherche          DicoCulture              Index alphabétique        Références      Brèves de Maths

      

Nombres

 

Débutants

Fractions

NOMBRES PÉRIODIQUES

 

Glossaire

Fractions

 

INDEX

 

Fractions

 

Représentation des nombres

 

Débutants

Tour d'horizon

Longueur de la période

Nombres décimaux

Nombres périodiques

Dichotomie de la période

Premiers longs

Nombres cycliques

Extraction des décimales

Fractions en 1/99…99

142 857

Égalité 0,999 = 1

Cas particuliers

 

Sommaire de cette page

>>> Trois cas pour l'exemple

>>> Caractérisation des nombres périodiques

>>> Liste des valeurs périodiques pour n < 100

>>> Permutations circulaires – Explications

>>> Période de la fraction a/b

>>> Bilan

>>> Anglais

 

 

 

 

 

NOMBRES PÉRIODIQUES

PERMUTATION des décimales

Nombres cycliques

 

Nous nous intéressons aux fractions en n / P où P est un nombre premier et n un nombre de 1 à n – 1.

Toutes ces fractions présentent un air de ressemblance avec des décimales qui "tournent en rond".

 

Un nombre cyclique est un nombre de n chiffres qui, lorsqu'il est multiplié par 1, 2, 3, …n, présente les mêmes chiffre mais dans un ordre différent (permutation circulaire)

 

 

Trois cas pour l'exemple

 

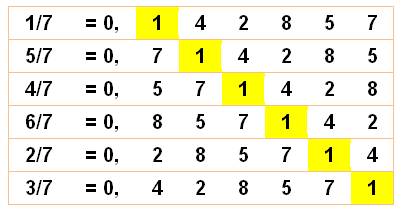
Fractions en 1/7 

   

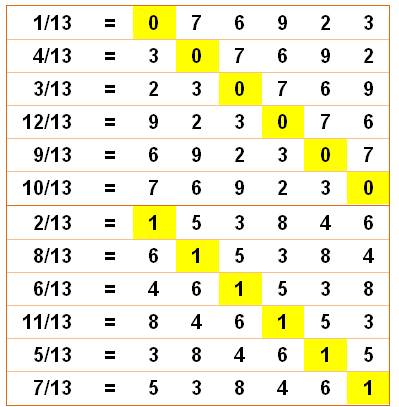
La période (142857) est la même pour toutes ces fractions. Elle est simplement décalée d'un rang ou plus selon la fraction. Les six fractions couvrent les six permutations circulaires possibles

 

Fractions en 1/13 

 

 

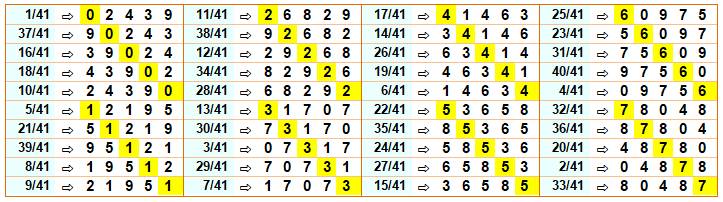
Deux périodes (076923 et 153846) sont nécessaires pour couvrir les douze fractions avec les permutations circulaires de ces deux nombres.

 

Fractions en 1/41

Le développement décimal de la fraction 1/41 a une période de longueur égale à 5. Pour couvrir les 40 fractions en n/41 par permutations circulaires, il faut 40 / 5 = 8 périodes.

  

 

Caractérisation des nombres périodiques

 

Un nombre périodique est donc caractérisé par:

*       la longueur de la période LC et

*       la quantité de périodes NC couvrant toutes les fractions

 

Exemple avec le nombre 13:  LC = 6 chiffres et NC = 2 périodes.

 

Liste de ces paramètres pour P = 2 à 103

En jaune, le cas des périodes maximale LC = P – 1 et dans ce cas NC = 1.

 

P

2

3

5

7

11

13

17

19

23

Nc

/

2

/

1

9

2

1

1

1

Lc

/

1

/

6

2

6

16

18

22

 

 

 

 

 

 

 

 

 

 

 

P

29

31

37

41

43

47

53

59

61

Nc

1

2

12

8

2

1

4

1

1

Lc

28

15

3

5

21

46

13

58

60

 

 

 

 

 

 

 

 

 

 

 

P

67

71

73

79

83

89

97

101

103

Nc

2

2

9

6

2

2

1

25

3

Lc

33

35

8

13

41

44

96

4

34

 

 

Dans tous les cas, bien évidemment:

Nc . Lc   =   P – 1

 

 

 

Liste des valeurs périodiques pour N < 100

 

Lire la liste

*    Avec 3, deux périodes: 1/3 = 0,333... et 2/3 = 0,666...

*    Avec 7, une seule période: 1/7 = 0,142857… et les autres fractons sont une permutation circulaire de celle-ci.

*    Etc.

 

Liste

 

3

3

6

7

14257

11

09

18

27

36

45

54

63

72

81

13

0769230

153846

17

0588235294117647

19

052631578947368421

23

0434782608695652173913

29

0344827586206896551724137931

31

032258064516129

096774193548387

37

027

054

081

135

162

189

243

297

378

459

486

567

41

02439

04878

07317

09756

12195

14634

26829

36585

43

023255813953488372093

046511627906976744186

47

0212765957446808510638297872340425531914893617

53

0188679245283

0377358490566

0754716981132

0943396226415

59

0169491525423728813559322033898305084745762711864406779661

61

016393442622950819672131147540983606557377049180327868852459

67

014925373134328358208955223880597029850746268656716417910447761194

71

0140845070422535211267605633802816909859154929577464788732394366197183

73

01369863

02739726

04109589

05479452

06849315

08219178

12328767

15068493

16438356

 

79

0126582278481

0253164556962

0379746835443

 

0506329113924

0759493670886

1518987341772

83

01204819277108433734939759036144578313253

02409638554216867469879518072289156626506

89

01123595505617977528089887640449438202247191

03370786516853932584269662921348314606741573

97

01030927835051546391752577319587628865979381443298969072164948 4536082474226804123711340206185567

 

Curiosité

10 / 81 = 0,1 2 3 4 5 6 7 9 0 0 1 2 3 4...
Note: il n'y a pas de "8".

Voir Autres cas / Table des périodes

  

 

 

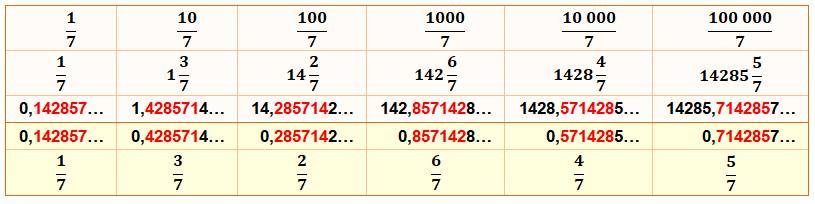
Permutations circulaires – Explications

 

Nous venons de voir que les fractions de même dénominateur partageaient les mêmes périodes à une permutation circulaire près.

 

Reprenons l'exemple des fractions en n/7

1/7 = 0,142857 142857 142857 ...

 

Formons le tableau suivant:

*       Ligne 1: les fractions en 10n / 7;

*       Ligne 2: les mêmes fractions en isolant la partie entière (1 3/7 = 1 + 3/7);

*       Ligne 3: le développement décimal de ces fractions;

*       Ligne 4: ces mêmes nombres tronqués de la partie entière; et

*       Ligne 5: les fractions sans la partie entière.

Non seulement nous retrouvons les périodes et leurs permutations circulaires, mais aussi une idée de leur apparition selon la valeur du numérateur

 

 

 

Période de la fraction a/b

 

*    Si une fraction 1/b a un développement périodique de longueur L, quelle est la longueur de la période pour la fraction irréductible a/b?

*    Avec l'exemple de 1/7, il semble que ce soit la même. Est-ce vrai?

 

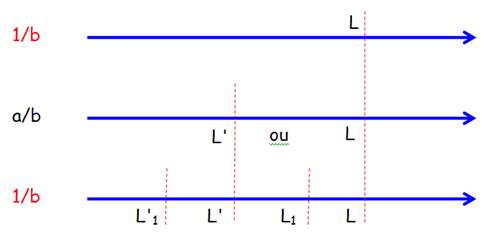
a/b par rapport à 1/b

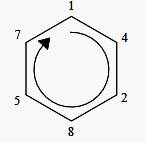
*    La période de la fraction a/b est celle de 1/b de toute manière, mais elle peut être plus petite (L').

 

Imaginez un engrenage de L dents, si la multiplication par a faisait tourner l'engrenage plus vite, la période serait un multiple de L et L resterait la période. Par contre, moins vite, la multiplication par a pourrait faire apparaître une périodicité sous-jacente inférieure à L. Est-ce possible?

 

1/b par rapport à a/b

*    La fraction a/b est irréductible. Alors, a et b sont étrangers. Et avec Bézout, on sait qu'il existe deux nombres x et y tels que ax + by = 1.

Alors: 1/b = (ax + by) / b = ax/b + y
Ce qui montre que la période de 1/b est la même que celle de a/b, ou alors inférieure: elle peut prendre les valeurs L ou inférieure (L1) ou L' ou inférieure (L'1).

*    Illustrons nos résultats

*    Ce schéma montre que la période de 1/b étant L, les autres valeurs n'existent pas. La période de a/b est également L.

 

 

 

 

Bilan

 

*    Exprimer une fraction par un nombre avec des décimales, c'est donner son développement décimal.

 

*    Soit une fraction irréductible:    (a et b sont étrangers).

 

*    Alors:

 

*    Si b = 2x x 5y  => le développement décimal est fini,

*    Sinon => le développement décimal est périodique.

*    Si le développement est périodique:

*    la longueur de la période est déterminée par 1/b,

*    si b est un multiple d'un nombre premier p, cette longueur est au maximum égale à p – 1.

*    avec un nombre premier: Nc . Lc = P – 1.

 

*    Lorsque le nombre a une période de longueur maximale, c'est un nombre premier long.

 

*    Le produit de la période par le nombre premier générateur est un repdigit en 9.  Ex: 1/7 = 0, 142857 … et 142 857 x 7 = 999 999

 

 

Anglais

A cyclic number is a number with n digits, which, when multiplied by 1, 2, 3, ..., n produces the same digits in a different order.

For example, 142857 is a cyclic number: 142857 × 2 = 285714; 142857 × 3 = 428571; 142857 × 4 = 571428; 142857 × 5 = 714285; 142857 × 6 = 857142, and so on.

It has been conjectured, but not yet proven, that an infinite number of cyclic numbers exist.

 

 

 

 

 

Retour

*   Premiers longs

*    Nombres périodiques

Suite

*   Extraction des décimales

*    Fraction 1/7  et magie du nombre 142 857

Voir

*    Nombres périodiques – Analyse de cas

*    Nombre magique 142857

*    Nombres têtus

Aussi

*    Calcul mental – Index

*    Clé de divisibilité

*    Fractions continues

*    Fractions de Farey

*    Géométrie – Index

*    Nombre 0,1347…

*    Nombres décimaux

*    Nombres premiers longs – Table

*    Nombres rationnels

*    Nombres têtus

*    Théorie des nombres – Index

Site

*    Nombres cycliques – Wikipédia

*    Artin's constant – Wolfram MathWorld

Cette page

http://villemin.gerard.free.fr/Wwwgvmm/Nombre/aaaCycli/NbCycPer.htm