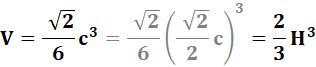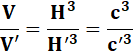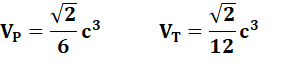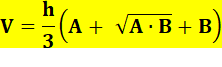|
|||||||||||||||||||||||||||||||||||||||
![]()
|
|
|
La forme même des pyramides d'Égypte, nous apprend que dès la plus haute
antiquité, les ouvriers avaient tendance à en faire de
moins en moins. |
Voir
Pensées & humour
|
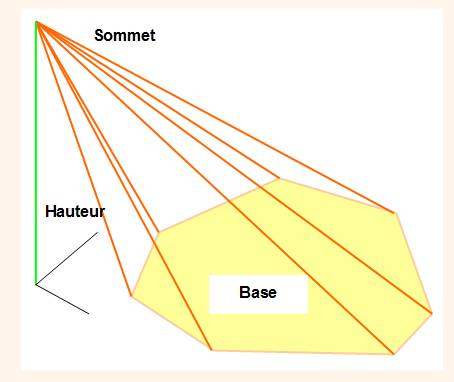
FORME |
|
|
|
|
|
|
|||||||||||||||||
|
|||||||||||||||||
|
|
||||||||||||||||||||||||||||
|
Calcul du volume
Dans
le cas où les faces sont simplement isocèles,
le volume des pyramides est dans le rapport du cube de leur hauteur ou de leur
côté.
|
||||||||||||||||||||||||||||
|
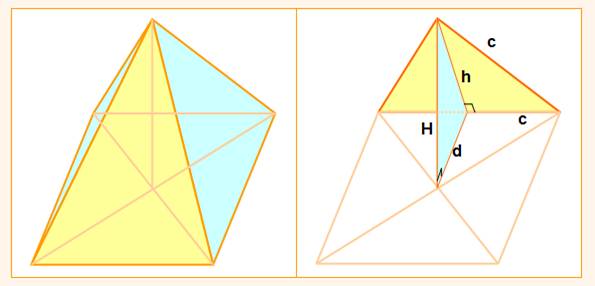
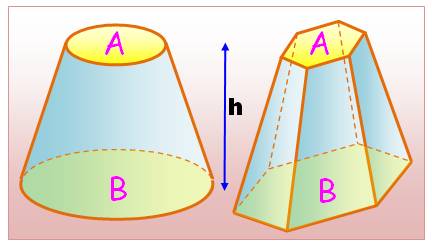
On compare le tétraèdre et
la pyramide à base carrée pour lesquels les triangles équilatéraux sont identiques.
Soit c la longueur des 14 côtes.
Le volume de la pyramide est le double
de celui du tétraèdre.
|
Voir Brève
680 / Cylindre,
cône et sphère – Comparaison
|
|
||||||||||||||||||||||||||||||||||
|
Calcul
du volume
Surface
|
||||||||||||||||||||||||||||||||||
|
|
||
|
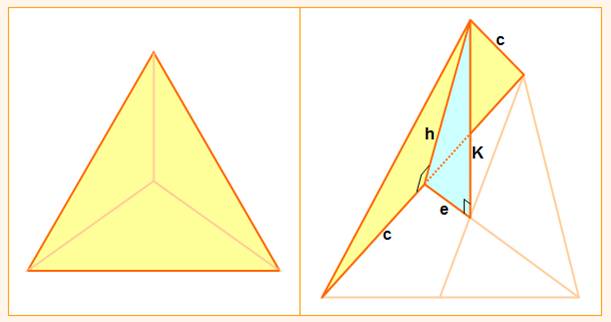
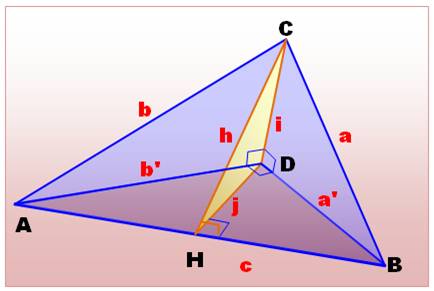
Nous nous
propososns d'évaluer l'aire de la face ABC par rapport aux trois autres
faces. La face
ABC est dite face "hypoténuse"
et les trois autres, faces latérales. Le point D peut être considéré comme la projection orthogonale de C sur le
plan ABD. CH et DH sont hauteurs dans les triangles ABC et ABD. |
|
|
|
Aire du triangle ABC |
AABC
= ½ AB x CH = ½ c . h |
|
|
Aire des
autres triangles |
AACD
= ½ i . b' ABCD
= ½ i . a' AABD = ½ j
. c |
|
|
Carrés
des aires des deux triangles du fond |
AACD2
+ ABCD2 = ¼ i²
(a'² + b'²) = ¼ i² . c² |
|
|
En
ajoutant le troisième |
AACD2 + ABCD2
+ AABD2 =
¼ c² (i² + j²) = ¼ c² .
h² = AABC2 |
|
|
Dans une pyramide triangulaire trirectangle, le carré de l'aire du
triangle "hypoténuse" est égal à la somme des carrés des aires des
trois autres triangles latéraux. |
||
Voir Théorème de Pythagore / Application aux projections
|
BONUS
sur les angles |
Alpha est l'angle dièdre entre les plans de ABC et ABD
(angle jaune en H sur la figure); Beta, idem
pour le dièdre ABC et ADC; Gamma, idem
pour le dièdre ABC et BDC. |
|
Aire des triangles projetés, avec S
aire du triangle ABC |
AACD
= S cos ABCD
= S cos AABD
= S cos |
|
La somme
des carrés des aires est égale
à S² selon ci-dessus => |
S² =
S² (cos² |
|
Conséquence |
cos² |
|
La
somme des carrés des cosinus des angles que fait un plan avec trois plans
rectangulaires est toujours égale à l'unité. |
|
|
Dans le
triangle jaune on trace la hauteur issue de D: DE |
Les angles de cette droite avec chacune des
droites du trièdre rectangle sont également alpha, bêta et gamma. |
|
Le
triangle ABC étant choisi à volonté sur les trois droites du trièdre, il est
possible de généraliser |
La somme des carrés
des cosinus des angles que fait une droite avec trois droites orthogonales
est égale à 1. |
Voir Sin² + Cos² = 1
|
|
||
|
Tronc de
pyramide: volume qui subsiste lorsqu'une pyramide est étêtée par une coupe
parallèle à la base. Quelle
que soit la forme de la surface de base, le volume du tronc est donné par cette
formule utilisant la moyenne
héronienne:
|
|
|
Anglais: frustrum / Conical frustrum and pyramidal frustrum
Voir Tronc
de cône
|
|
|
|
Vente
pyramidale
En commençant
avec 6 initiateurs, les suivants sont 36 (6 x 6); et au dixième niveau, on trouve déjà
plus de 60 millions de personnes (610 = 60 466 176),
en gros, la population française. Système
de Ponzi
|
|
Anglais: Ponzi scheme
Humour
|
Le président
Sadi-Carnot (1837-1894), alors élève à polytechnique, injurie une marchande
de poissons qui avait taché son uniforme: Va donc eh! Pyramide tronquée, octaèdre
irrégulier, cycloïde
de révolution, équation usée, sinus décroissant ! Le
commissaire de police fut incapable de dire si ces expressions pouvaient être considérées comme des injures publiques. |
Voir Pensées et Humour
|
|
![]()
|
Index Pyramide |
|
|
Suite |
|
|
Voir |
|
|
DicoNombre |
|
|
Cette page |
![]()