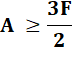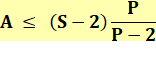Graphe planaire

Édition du: 02/04/2023

INDEX Graphe Topologie Logique	GRAPHES
	Graphes – Introduction	Arbres – Introduction	Chemin le plus court
	Chemin eulérien	Cinq pays	Voyageur de commerce
	Graphe planaire	Trois maisons	Multiple et diviseurs
	Graphe de Delaunay	Petit monde	Nombres de Delannoy
	Ivrogne	Colonies de fourmis

Faites un double-clic pour un retour en haut de page

GRAPHES PLANAIRES

Des circuits qui ne se croisent jamais. C'est le cas des circuits imprimés. Le courant doit aller d'un point à un autre en parcourant une piste sans croiser une autre piste. Ce n'est pas toujours possible. Il faut alors ajouter une nouvelle couche de circuits. Le plus simple étant le double-face, mais certains circuits complexes peuvent compter huit ou dix couches.

Sommaire de cette page

>>> Approche

>>> Définitions

>>> Relations

>>> Propriétés avancées

>>> English corner

Débutants

Dénombrement

Glossaire

Combinatoire

Circuits imprimés multicouches; multilayer printed circuit board

Quelques types de graphes

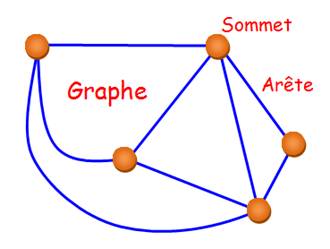
Graphe complet: tous les sommets sont reliés entre eux. Avec n sommets, le graphe comporte n (n – 1) / 2 arêtes.

Graphe k-facteur: chaque sommet ne reçoit que k arêtes.

Graphe planaire: sur un plan, les arêtes ne se croisent jamais.

Voir Exemple et emploi de graphes complets et 1-facteur / Vocabulaire des graphes

Approche
Des points et des arcs entre certains points: c'est un graphe. Dessiné sur une feuille, il est dans le plan: c'est un graphe plan Aucun des segments ne se croisent: le graphe plan est planaire.	Sommet ou nœud; Arête ou arc.
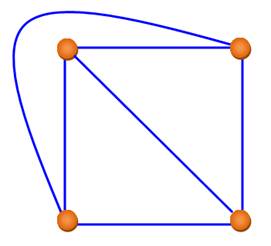
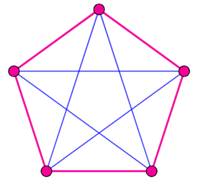
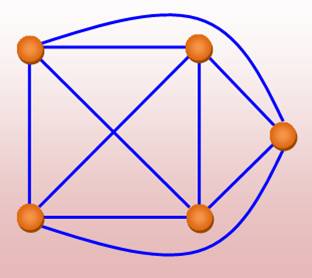
Dessinez quatre points et relier les de toutes les façons possibles sans croiser les arêtes. Un carré et une diagonale conviennent. La deuxième diagonale ne convient pas: elle coupe la première. Facile de dessiner une arête courbe qui contourne.
Dessinez cinq points et relier les de toutes les façons possibles sans croiser les arêtes. Essayez toutes les possibilités. vous n'y arriverez pas! Ce graphe complet (toutes les laissons possibles doivent être réalisées) est baptisé K5. Le graphe K5 n'est pas planaire.

Démonstration

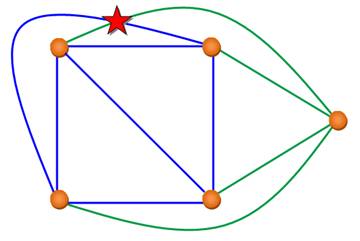
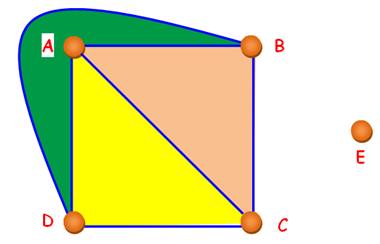
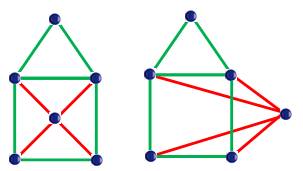
Il est facile de montrer que K5 est non-planaire.

Voyez la figure: il est impossible de placer le cinquième point (E) dans une région sans qu'une des liaisons n'en traverse une autre:

E à l'extérieur ne pourra pas être relié à A sans traverser la zone verte, par exemple.

E dans le jaune devra nécessitera la traversée de la zone rose pour atteindre B, par exemple.

Etc.

Autre démonstration >>>

Voir la célèbre énigme du Pont de Königsberg

Graphe K3,3 et autres

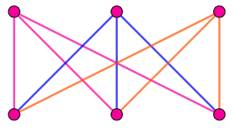
Le deuxième graphe planaire impossible est le K3,3. Un exemple est donné par l'énigme des trois maisons. Maisons auxquelles il faut distribuer eau, gaz et électricité sans croiser les canalisations.

Exemples de graphes complets

K3,3	K5	K4,2,2

Un graphe comme K5 est dit complet: un sommet est relié à chacun des autres. Il est unique pour tout Kn.

Un graphe comme K3, 3 est un graphe biparti complet: un sommet d'un groupe est relié à chaque sommet de l'autre groupe.

Voir Nombres chromatiques

Définitions
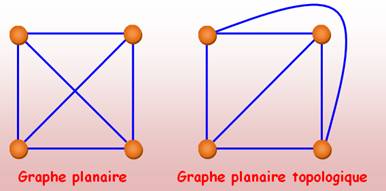
Un graphe planaire (topologique) est un graphe qui ne peut pas être dessiné sur un plan sans croisement. Graphe tel que deux arêtes quelconques ne se rencontrent qu'à leurs extrémités.	Étant donné un graphe, dès qu'on peut trouver une configuration planaire, le graphe est planaire. Par contre, dire qu'un graphe n'est pas planaire n'est pas facile. Jusqu'où faut-il chercher? Quand a-t-on épuisé toutes les possibilités?
Un graphe planaire peut se cacher. Un nouveau dessin en déplaçant les sommets et en respectant les liaisons entre sommets peut le révéler.	Autre exemple
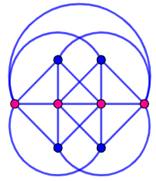
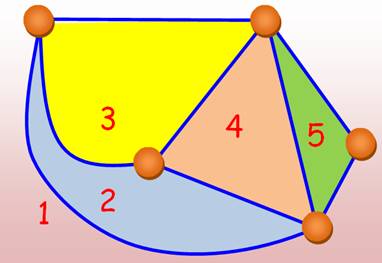
Les arêtes sont des segments linéaires ou courbes (on évite les boucles, sans intérêt!). Les arêtes délimitent des régions qui sont appelées: faces. La quantité de sommets est l'ordre du graphe. La quantité d'arêtes attachées à un sommet est le degré du sommet. La somme de tous les degrés est égale au double du nombre d'arêtes.	Graphe d'ordre 5 qui comporte cinq faces, sans oublier celle externe. Il a: 1 sommet de degré 2; 2 de degré 3; 2 de degré 4.

Voir Types de graphes

Relations

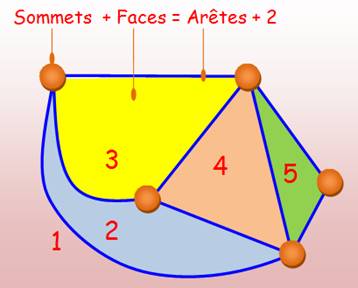
Théorème de Descartes-Euler

Pour un graphe planaire connexe (d'un seul tenant):

S + F = A + 2

Faces + Sommets = Arêtes + 2.

Relation degrés et faces

Pour un graphe quelconque:

= 2 A

Somme des degrés des sommets = deux fois la quantité d'arêtes. Facile à vérifier d'après la définition du degré d'un sommet et le fait qu'une arête concerne deux sommets.

5 faces, 5 sommets et 8 arêtes

On vérifie que: 5 + 5 = 8 + 2

Somme degrés: 2 + 3 + 3 + 4 + 4 = 16

Quantité de faces: 8

On vérifie: 16 = 2 x 8

Chaque face est entourée de trois arêtes.

Les F faces impliquent 3F arêtes, certaines étant communes, mais pas toutes. D'où l'inégalité indiquée.

Avec la relation de Descartes-Euler.

Soit l'inégalité indiquée.

Et la conclusion importante.

F = A + 2 – S

Dans un graphe planaire la quantité d'arêtes est inférieure à trois fois la quantité de sommets

Application

Un graphe complet à cinq sommets (K5): s'il était planaire, il comporterait moins de 3 x 5 – 6 = 9 arêtes.

Or, comptez bien, il y en a 10.

Le graphe K5 ne peut pas être planaire.

Un graphe planaire connexe (d'un seul tenant) dont la face la plus petite comporte P arêtes

La somme des arêtes des faces est égale deux fois la quantité d'arêtes. Il y en aura au minimum: P.F 2A.

Avec la relation de Descartes-Euler:

2A P (A + 2 – S)

2A PA + 2P – PS)

2A PA + 2P – PS

PA – 2A PS – 2P

A(P – 2) P(S – 2)

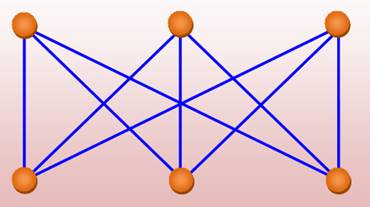
Un graphe planaire connexe sans triangle contient au plus:

A 2S – 4

Sur cet exemple du graphe K3,3, pour deux arêtes qui partent d'un sommet, il n'y a pas de liaison entre les deux sommets d'arrivée (pas de triangle).

Nous comptons 9 arêtes pour 6 sommets. Or 9 > 12 – 4 = 8.

Le graphe K3,3 n'est pas planaire

Sans triangle, les faces comportent au moins 4 arêtes. Avec P = 4, la relation précédente devient:

2A 4(S – 2)

Propriétés avancées
Les deux graphes non planaires (K3,3 et K5) sont caractéristiques de la non-planéarité. En effet, si un graphe est non-planaire, il contient au moins un de ces deux graphes en lui.	Théorème de Casimir Kuratowski (1929) Un graphe est planaire si et seulement si l'on ne peut en extraire aucun graphe du type K3,3 ou K5.
Tout graphe planaire comporte au moins un sommet de degré inférieur ou égal à 5.

English corner

When a connected graph can be drawn without any edges crossing, it is called planar. When a planar graph is drawn in this way, it divides the plane into regions called faces.

Euler's Formula for Planar Graphs: for any connected planar graph with

v vertices, e edges and f faces, we have: v – e + f = 2.

Voir Anglais pour le bac et pour les affaires

Retour	Graphes – Introduction Graphes – Index
Suite	Chemin le plus court Vocabulaire des graphes Coloration des graphes (nombre chromatique)	Graphes et problèmes NP Petit monde Sept amis autour d'une table
Voir	Code Gray Croissance logistique Énigmes et paradoxes Graphe de Delaunay Intelligence artificielle Jeux – Index	Logique formelle Percolation Relier les points d'un seul coup de crayon Topologie – Glossaire Tour de Brahmâ Trois maisons (énigme des -)
Site	Graphe complet – Wikipédia Références générales
Livre	Le problème de la fabrique de brique – Jean-Paul Delahaye – Pour la Science – n° 424 – Février 2013
Cette page	http://villemin.gerard.free.fr/aMaths/Topologi/aaaGraph/Planaire.htm