|
Édition du: 03/03/2023 |
|
INDEX |
Types de Nombres – Motifs |
|||
|
Zigzag (Euler) |
||||
![]()
|
PERMUTATIONS à MOTIFS ou sous-permutations Permutations
comportant ou non un motif d'ordre. Par exemple, le motif 123 qui signifie
qu'une suite de trois éléments dans l'ensemble ne sera du type x < y < z. Ce sujet
est d'une importance telle qu'une conférence a lieu tous les ans (The
International Conference on Permutation Patterns). Celle de 2023 a eu lieu à
Dijon. |
||
|
|
Sommaire de cette page >>> Approche >>> Permutations avec 4 nombres >>> Permutations avec 5 nombres |
Débutants Glossaire |
Anglais: Permutation pattern
|
Une permutation qui évite
123 ne contiendra jamais ce motif. |
Avec trois nombres, il y a six permutations: Elles
sont toutes retenues sauf celle qui précisément est 123. |
|
|
Le principe s'étend aussi à tout motif tel que
xyz qui revêt le même ordre que 123. Autrement-dit: x < y < z Et cela, même avec des nombres intermédiaires. |
Exemples avec cinq nombres |
|
|
On
cherche à connaitre la quantité de permutations de (1, 2, …, n) qui ne
contiennent pas une suite de trois nombres successifs permutés. Exemple ici:
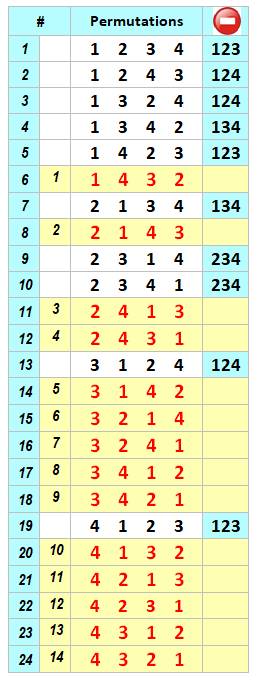
motif 123 Avec quatre nombres (1, 2, 3, 4) il y a 4! = 24 permutations mais seulement 14 évitent le
motif 123. Le nombre 14 est le quatrième nombre de Catalan. La quantité de
permutations pour n nombres est le nième nombre de Catalan Le tableau ci-contre montre toutes les permutations et, en colonne
de droite, on note les configurations interdites: tous motifs parmi les
quatre nombres tels que trois d'entre d'eux sont croissants. En
rouge, les permutations qui évitent le motif 123. |
|
|
|
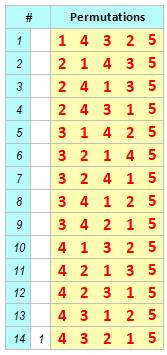
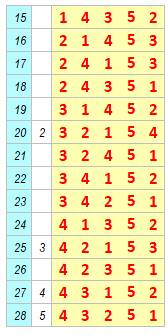
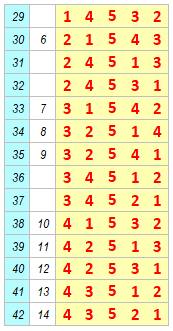
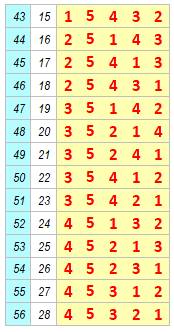
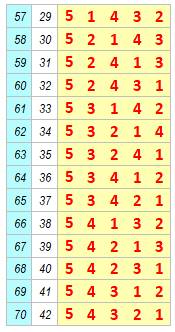
Avec cinq nombres (1, 2, 3, 4, 5) il y a 5! =
120 permutations mais seulement 42
évitent le motif 123, et on a bien le nombre de Catalan: C5 = 42. Construction On
retient les 14 configurations à 4 nombres et on ajoute la colonne de 5 en
chacune des cinq colonnes possibles; soit 5 × 14 = 70 lignes. Les permutations valides
sont parmi elles. On en détecte 42 qui évitent le motif 123.
|
|
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Sites |
|
|
Cette page |