![]()
|
|
Ce site est désormais accessible en http://diconombre.fr/index.html et
pour cette page voir le lien en fin de page For this page,
refer to the link at the bottom. |
|
22 Novembre 2025
![]()
|
|||||||||||||||||||||||||||||||||||||||||||||
![]()
|
Aire de la PROJECTION des triangles Comment calculer l'aire projetée d'un triangle, d'un polygone. Formules et détails du calcul. |
|
|
||
|
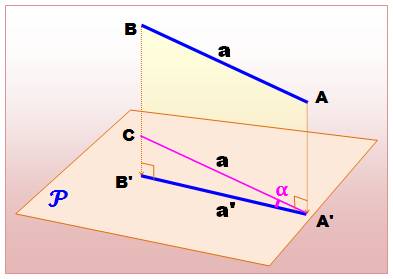
Projection
orthogonale du segment AB sur le plan P. Quelle est la longueur du segment
résultant, le segment projeté A'B'. Des
points A et B on descend des perpendiculaires au plan P qui prennent pied en
A' et B'. Le plan ABB'A' est orthogonal au plan P. On trace
A'C, la parallèle à AB qui passe par A'. Elle fait un angle alpha avec la
droite |
|
|
|
Dans le
triangle A'B'C |
a' = a cos |
|
|
dont un côté est parallèle au plan de projection |
|
|
|
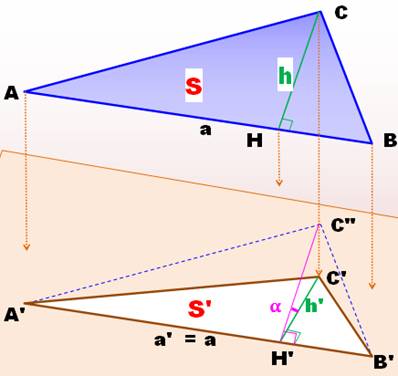
Cas du
triangle ABC dont le côté AB est parallèle au plan de projection. Une de
ses hauteurs CH. Ces
quatre points ABCH sont projetés sur le plan en A'B'C'H'. Le triangle
A'B'C" (pointillés bleus) est parallèle et congruent au triangle ABC
initial. Il sert à définir l'angle alpha. La
projection conserve les perpendiculaires et C'H' est une hauteur du triangle
A'B'C'. Elle conserve également la
longueur a pour A'B' parallèle à
AB. |
|
|
|
Aire du
triangle ABC |
A = ½ h . a |
|
|
Aire du
triangle A'B'C', avec a = a' |
A' = ½ h' . a' = ½ h' . a |
|
|
Le
segment CH est projeté en C'H' |
h' = h cos |
|
|
En
remplaçant |
A' = ½ h . a cos A' = A cos |
|
|
Imaginez
ABC comme une porte avec une charnière en AB. Voir Relativité – Image de la porte
entrebâillée |
L'aire
de la porte vue par un obsevateur fixe (la projection de ABC) varie comme le
cosinus de l'angle d'ouverture. |
|
|
|
||
|
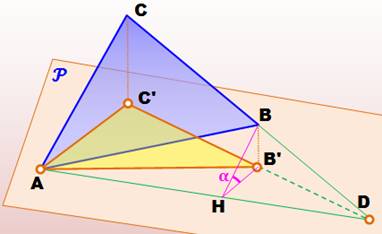
Un
triangle ABC quelconque par rapport au plan de projection P, lequel à été
translaté pour contenir le point A. Le plan
du triangle fait un angle alpha avec le plan P (angle du dièdre). Le
triangle ABC se projette en AB'C'. |
|
|
|
Triangle
ABD: il fait un angle alpha avec le plan P |
AAB'D = AABD cos |
|
|
Triangle
ACD: il fait un angle alpha avec le plan P |
AAC'D = AACD cos |
|
|
Triangle
AB'C' = différence entre les deux |
AAB'C' = (AACD
– AABD) cos |
|
|
Finalement |
AAB'C' = AABC cos |
|
|
Dans tous les cas, l'aire de la
projection d'un triangle est égale au produit de l'aire du triangle par le cosinus
de l'angle du dièdre formé par les deux plans (le plan de projection et celui
du triangle). Un polygone se
décompose en triangles. Ainsi l'aire de la projection d'un polyone suit la même
loi en cosinus. Un figure courbe plane (un disque,
une ellipse …) peut etre vue comme un polygone à une infinité de côté. L'aire
de sa projection suit la même loi en cosinus. Le carré de l'aire d'une figure
plane est égal à la somme des carrés des aires des trois projections de
la figure sur trois plans orthogonaux. |
||
![]()
|
Suite |
|
|
Voir |
|
![]()