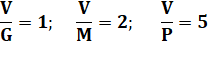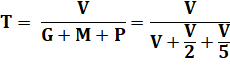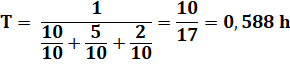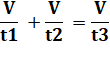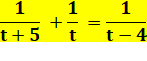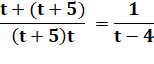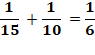|
||||||||||||||||||||||||||||||||||||||||
![]()
|
Problèmes de Robinets
Problèmes qui font peur. Pourtant simple à
résoudre en s'y prenant par le bon bout. |
|
Pourquoi
harcèle-t-on les enfants avec des problèmes de baignoires dont le robinet
débite 56 litres à la minute tandis que ne s'écoulent que 6,7 décilitres à la
seconde quand on sait pertinemment que dans la vie il suffit de fermer le
robinet pour ne pas s'emmerder avec de l'eau qui déborde ? Geluck enfonce le clou de Philippe Geluck |
Voir Pensées & humour
Attention
|
Les
problèmes de vitesses et de débits n'ont
pas de réponses immédiates |
|
LE
TRUC ! Il
f l ou un volume à remplir (Volume = d.t). |
Voir Problème de robinets résolu pas à pas
![]()
|
|
||
|
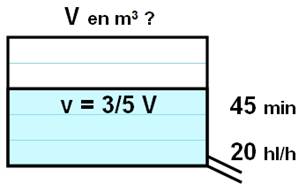
Problème (Certificat d’études 1923) Une pompe
d’épuisement a vidé les 3/5 d’un bassin en 45 minutes, en débitant 20 hl à
l’heure. Quelle est, en mètres cubes, la contenance de ce bassin ? |
|
|
|
Solution: volume d'eau écoulée En une heure, il s'écoule 20 hl d'eau. En 45 minutes (3/4 heure), on aura un peu moins:
v = 20 x 3/4 = 15 hl. |
Solution: volume du bassin Cela représente les 3/5 du bassin. Le bassin
contient un peu plus d'eau: 15 x 5/3 = 25 hl. Un hectolitre = 100 litres: V = 25 hl = 2500
litres. Un m3 = 1000 litres: V = 2500 l = 2,5
m3. |
|
Voir Niveau en maths
et autres exemples de problèmes de ce niveau
|
|
||
|
Problème Un camion part pour sa
livraison à 8 h. Il constate une consommation
anormale de gazole à 10 h. Il ne lui reste plus que 20 litres. Il décide de faire demi-tour,
mais n'arrive pas à rejoindre son dépôt. À 10h 20 c'est la panne sèche. Sa consommation est
constante et la fuite est régulière. Quel est la capacité du
réservoir du camion? |
Solution Après demi-tour,
la consommation et la fuite consomment le total des 20 litres qui restaient
dans le réservoir, et cela en 20 minutes. Soit 1 litre par minute. Durant
la première partie du trajet qui dure 120 minutes, il consomme (moteur + fuite): 120 x 1 = 120 litres. La
capacité du réservoir, égale à la totalité de la consommation, vaut: C = 20
+ 120 = 140 litres. |
|
|
|
||
|
Problème Une cuve et trois robinets.
Avec le Gros robinet la cuve se vide en 1 heure; avec le Moyen en 2 heures et
avec le Petit, il faut 5 heures. Les trois robinets sont ouverts, combien de
temps faudra-t-il pour viser la cuve? |
|
|
|
Méthode classique |
Méthode de la fausse
position |
|
|
V = volume de la
cuve. G, M, P = débits
des robinets. T = durée de
vidange de la cuve avec les trois robinets ouverts.
Soit 0,588 x 60 = 35,29 minutes = 35 min 17,64 s |
Hypothèse (fausse sans
doute): T = 10 h Avec G, la cuve se viderait
10 fois; Avec M, elle se
viderait 5 fois; Avec P, ce serait 2 fois. Avec les trois, en 10 h, elle se viderait 17 fois. Elle se vide en 10/17
heures. |
|
Voir Fractions / Poids du tonneau
Autre exemple de calcul par fausse position
|
Combien de blocs de 45 kilos équivalent à 100 blocs de 10 kilos ? Supposons que la réponse soit 180, correspondant à 4 fois les 45
kilos. Pour arriver à 100 sur 10 = 10, il faut multiplier par 2,5 (ou 5/2). Ce qui donne 180 x 5 / 2 = 450. La méthode moderne donnerait immédiatement: x/45 = 100/10 => x =
450. Cet exemple est donné par le scribe Ahmès (vers – 1500) dans le papyrus
Rhind. |
|
Problème Un étang est alimenté par trois rivières
R1, R2 et R3. Combien de temps faut-il aux trois rivières
pour remplir l'étang?. |
Seule, chaque rivière
remplirait l'étang en: R1 => 1 jour R2 => 2 jours R3 => 3 jours |
|
|
Solution La valeur constante ici est le volume du bassin. Ce qui est spécifique c'est le débit de chaque
rivière et la durée du remplissage. Si le débit de l Sur une durée de 1 jour (24h), il s'écoule 24 m3
qui serait la contenance (le volume) de l'étang. Autrement dit la formule est bien: V = d x T (Volume = débit x temps) Si deux rivières coulent ensemble, l'une V = (d1 + d2) x T |
||
|
Formule appliquée dans les trois cas
connus: et pour celui inconnu, pour lequel les
trois rivières sont en action. |
V = d1 x 1 jour V = d2 x 2 V = d3 x 3 V = (d1 + d2 + d3) x T |
|
|
Des trois premières équations, tirons la valeur du débit. Que nous plaçons dans la
quatrième équation. Et après simplification
par V. Afin d'obtenir la durée
demandée: |
d1 = V / 1 d2 = V / 2 d3 = V / 3 V = V (1/1 +1/2 + 1/3) T 1 = 1
(6/6 + 3/6 + 2/6) T 1 = 11 / 6
x T T = 6 / 11 jour
≈ 13,1 heures |
|
|
Méthode de la fausse
position |
Hypothèse: 6 jours Avec R1,
l'étang est rempli 6 fois Avec R2,
l'étang est rempli 3 fois Avec R3,
l'étang est rempli 2 fois Avec les trois, 11 fois
en 6 jours Soit une fois en 6/11
jour |
|
Problème connu des
|
Problème Trois robinets et une cuve. Combien de temps pour remplir l |
On remplit l en 1h 12 en 1h 30 en 2h avec le moyen et le
petit. |
||
|
Méthode de la fausse
position |
Compte-tenu
des trois nombres (72, 90 et 120 minutes), on imagine que la réponse est 360
minutes, le PGCD des trois nombres:
Rappel: on conserve
tous les facteurs et on leur attribue l'exposant le plus élevé de tous. Alors
en 320 minutes: G
+ M remplissent la cuve 5 fois (5 x
72 = 360); G
+ P remplissent la cuve 4 fois (4
x 90 = 360); M
+ P remplissent la cuve 3 fois (3 x
120 = 360); Total
de ces débits: 2
(G + M + P) ⇨
12 fois la cuve en 360 minutes Les
trois remplissent la cuve en 360
/ (2 x12) = 60 min. |
||
|
Solution classique
La réponse est 1 heure.
Pas évident tout de suite! Le calcul est un peu long. C
On
remarque que 3 divise tous les numérateurs, de même que 4 et 5. Les
numérateurs sont divisibles par 3 x 4 x 5 = 60. Ayant
été mis au même dénominateur, on peut les ajouter.
Note: on aurait pu calculer le plus grand commun
diviseur (PGCD). PGCD
(72, 90, 120) 72 = 2 x 2 x 2 x 3 x 3 90 = 2 x 3 x 5 120 = 2 x 2 x 2 x 3 x 5 PGCD =
2 x 3 Pour
simplifier les fractions par 6 directement.
Dans ce
cas, on observe que le gain de temps de calcul n'est pas notable. |
|
|
||
|
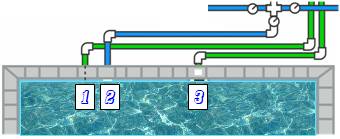
On dispose de trois tuyaux de débit constant pour remplir la
piscine. Avec les deux premiers,
utilisés simultanément, il faut le même temps Le 2e tuyau
la remplit en 5 heures de moins que le premier et en 4 heures de plus que le
3e Quelle est la durée de
remplissage pour chaque tuyau seul ? |
||
|
Relations La somme des débits d1 et d2 vaut le débit d3. Pour remplir le volume V de la piscine avec un débit d il faut
un temps t: V = d.t d'où:
d = V / t. Peu importe, la valeur du volume, il note qu'il se simplifie
dans l'égalité. On sait que, par rapport à t2 = t, Cette relation (en
jaune)
ne présente plus qu'une seule inconnue t, que nous allons calculer. |
|
|
|
Résolution On réduit
au même dénominateur la partie de gauche. Puis on,
transforme l'égalité par un produit en croix. En simplifiant,
il reste une équation du deuxième degré. On sait
que le terme constant (- 20) est le produit des racines et le coefficient
de t (+8) en est la somme. Les nombre
10 et -2 répondent à ces égalités de produit et somme. Seule la valeur
positive (10) est à retenir pour une durée. |
(2t + 5) (t – 4) = (t + 5) t t² – 8t – 20 = 0 t = 10 ou t = – 2 |
|
|
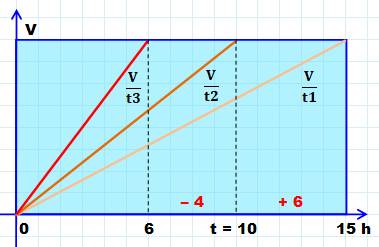
Illustration
|
Solution t1 = 15 h t2 = t =
10 h t3 = 6 h Quels que
soient les débits ou le volume de la piscine. Vérification
|
|
Voir Nombre
1/6 = 0,1666…
![]()
|
Voir |
|
|
Aussi |
|
|
Cette page |
http://villemin.gerard.free.fr/aScience/Vitesse/Robinets.htm |