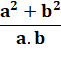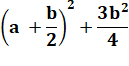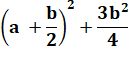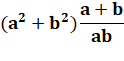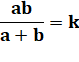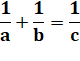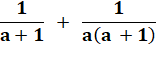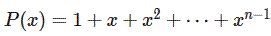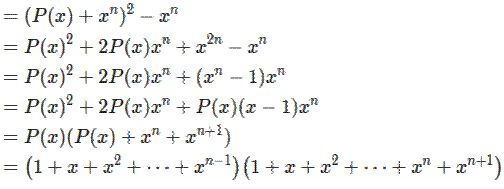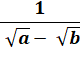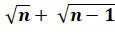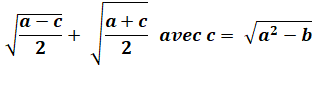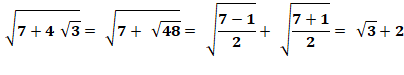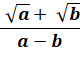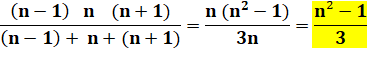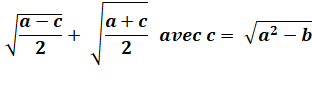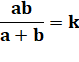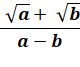NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 01/02/2024 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Algèbre
Débutants Algèbre	IDENTITÉS			Glossaire Algèbre
INDEX Identités Algèbre	Remarquables	Degré > 2	Spéciales	Divers
	Inverses	a^n – b^n (moins)	a^n – 1	Complexes
	Puissances	a^n + b^n (plus)	(x+ x² + …) ^k	Trigonométrie
	Newton	Puissance 5	Héron	Moivre
	Dévelop. limités	Euler & Riemann	Racines (degré 1/n)	(a + b + c + d)^k
	Ramanujan	Degré 7	Polynômes symétriques élémentaires
		Sommaire de cette page >>> Identités remarquables – Premier degré >>> Identités remarquables – Deuxième degré >>> Identités (a + b)² = a² + 2ab + b² … >>> Consécutifs >>> Formule de De Moivre >>> Complexe

Humour

Belle égalité en rébus Moins de HAINE égal plus de PAIX	Une autre égalité déroutante, à découvrir

Voir Pensées et humour / Alphabet parlant / Paradoxe du pastis

IDENTITÉS REMARQUABLES

& Formules à noter

Les classiques du collège et les moins connues (identités ou formules) …

Les trois reines (plus une en complexe)

Factorisation des différences de puissance

Voir Table pour n de 2 à 20 et applications à aⁿ – 1

Identité cachée (différence de deux carrés)

Voir Puissances à étages

Voir Exemple de technique opératoire avec les parenthèses / Complexes et carrés /

Démonstration de la formule de Héron

IDENTITÉS avec le 1^er degré
(a + b) (x + y)	=	ax + ay + bx+ by
(10a + b) (10x + y)	=	100 ax + 10(ay + bx) + by
(a + x) (a + y)	=	a (a + x + y) + xy
(a + b + c) (x + y + z)	=	ax + ay + az + bx + by + bz + cx + cy + cz
(100a + 10b + c) (100x + 10y + z)	=	10000 ax + 1000 (ay + bx) + 100 (az + by + cx) + 10 (bz + cy) + 1 (cz)

Voir Applications au calcul rapide des multiplications

Curiosités

(n + 1)² – (n – 1)² = 4n (n + 2)² – (n – 2)² = 8n (n + 3)² – (n – 3)² = 12n …

n = 100 101² – 99² = 400 102² – 98² = 800 103² – 97² = 1200

Voir Nombres pairs et impairs

IDENTITÉS avec le 2^e degré
a² + b²	=	½ (a + b)² + ½ (a – b)²
a² + b² avec 2ab = c²	=	(a + b – c) (a + b + c)
(a + b)² + (a – b)²	=	2 (a² + b²) Trigo >>>
(a + b)² – (a – b)²	=	4 ab
(a + b)² × (a – b)²	=	a^4 – 2a²b² + b^4
(a + b)² / (a – b)²		pas intéressant
	=
(a + b)²	=	(a – b)² + 4ab (Problème de Viète)

Merci à Mehdi R.

(a + b + c)²	=	a² + b² + c² + 2ab + 2bc + 2ca
(a + b + c + d)²	=	a² + b² + c² + d² + 2ab + 2ac + 2ad + 2bc + 2bd + 2cd
(a + b + c + d + …)²	=	a² + b² + c² + d² + … + 2ab + 2ac + 2ad + … + 2bc + 2bd + … + 2cd + …

Voir Calcul du carré des nombres à n chiffres

(a + b)² + (b + c)² + (c + a)²	= =	2 (a² + b² + c² + ab + bc + ca) (a + b + c)² + a² + b² + c²
(a + b + c)² – (a – b + c)²	=	4 ab + 4 bc
(a + b + c)² – (a – b – c)²	=	4 ab + 4 ac
a² (b – c) + b² (c – a) + c² (a – b)	=	(a – c) (b – a) (c – b)

Démonstration

(a² + b²)^2	=	(a² – b²)^2 + (2ab)^2
(a + b)^2 (a – b)^2	=	(a² + b²)^2 – (2ab)^2
(a² – 2ab – b²) (a² + 2ab – b²)	=	(a² – b²)^2 – (2ab)^2
a² + ab + b²	=
	=

Parfois utile, même si trivial

ab	=	(a + 1)b – b
a(b + 1)	=	ab + a

Identités de Lagrange (dites aussi de Fibonacci – 1202)

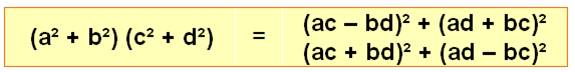
L'inversion des signes + et - ne change pas l'égalité

Voir Somme de carrés/ Autres identités de cette sorte

a, b, c > 0

a + ab + b + 1	=	(a + 1) (b + 1)
a² – 1	=	(a + 1) (a – 1)
a^3 – 1	=	(a – 1) (1 + a + a² )
a^3 + 1	=	(a + 1) (1 – a + a² )
a^6 – 1	=	(a + 1) (a – 1) (a² + a + 1) (a² – a + 1)

	<=>	c² = uv avec a = c + u et b = c + v
	=
	<=>	(a – k) (b – k) = k²
	=
	=	Voir Somme des inverses et généralisation
ab (a² – b²) + bc (b² – c²) + ca (c² – a²)	=	– (a – b) (b – c) (c – a) (a + b + c)

(1 + x)² – x	=	1 + x + x²
(1 + x + x²)^2 – x²	=	(1 + x) (1 + x + x² + x^3) (1 + x)^2 (1 + x²)
(1 + x + x² + x^3)^2 – x^3	=	(1 + x + x²) (1 + x² + x^3 + x^4)
(1 + x + x² + … + x^n)^2 – x^n	=	(1 + x + x² + … + x^n – 1) (1 + x + x² + … + x^n + 1)

Démonstration

On pose :

On calcule:

.

Racine ou puissance 1/2

	=
	=	Voir Application
	=
Exemple

Voir suite en Degré supérieur / Calcul avec des radicaux (racines) / Calculs avec les racines carrées

Voir Factorisation des polynômes remarquables / Exemples d'application /

Calcul de la hauteur du pentagone (calculs avec radicaux)

Démonstration muette (ou illustrée)

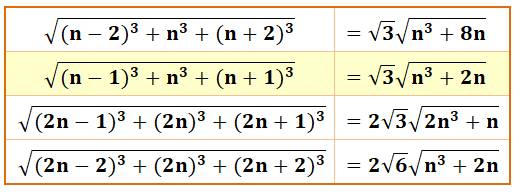
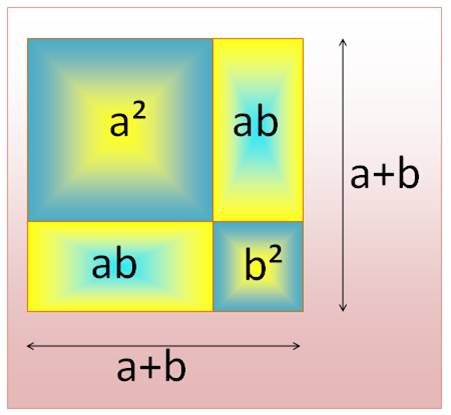
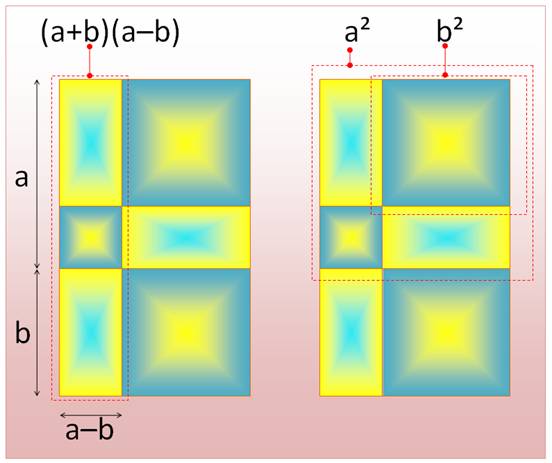
L'aire du grand carré (a + b) est égale à la somme des aires des deux carrés et des deux rectangles: (a + b)² = a² + 2ab + b² L'aire du rectangle vertical est égale à la somme des aires du petit carré et des deux rectangles; elle est aussi égale à l'aire d'un grand carré (a²) auquel on retire un plus petit carré (b²). (a + b) (a – b) = a² – b² Aire du rectangle à gauche = aire e l'équerre à droite.

Voir Nombre 169 / Construction de a², racine de a, 1/a / Calcul de la racine carrée

Produit de nombres consécutifs
(n – 1) n (n + 1) = n (n² – 1) = n^3 – n (n – 2) (n – 1) n (n + 1) (n + 2) = n (n^4 – 5n^2 + 4) (n – 3) (n – 2) (n – 1) n (n + 1) (n + 2) (n+3) = n (n^6 – 14n^4 + 49n^2 - 36) Note: ces produits sont divisibles par n, le facteur central, et par k, la quantité de termes (impaire) Ainsi: 5 x 6 x 7 x 8 x 9 = 15 120 = 7 x 5 x 432

Voir Calcul mental et factorielles tronquées / Divisibilité des produits de nombres consécutifs

FORMULE de MOIVRE

Suite Formule de De Moivre

IDENTITÉS avec complexes
x² + y²	=	(x – i . y) (x + i . y)
y = 1 => x² + 1	=	(x – i) (x + i)
x = 1 => 1² + 1	=	(1 – i) (1 + i) = 2

Suite Pages des nombres complexes / Nombre 2

Suite	Identités pour degré supérieur à 2 Cube – Calcul mental Formule du binôme Somme des entiers, des carrés, des inverses… Identité de Brahmagupta Identités fractions Identités trigonométriques Identités nombres complexes Identités entre puissances Utilisation pour calcul de puissances complexes
Voir	Application aux multiplications Applications aux divisions des puissances Carré des nombres en aaa…ab Constantes Différences entre puissances Égalités dans les triangles Factorisation selon Fermat Formulaires – Index Identité de Lagrange Identités trigonométriques Isopérimètre Pépites Somme de carrés de nombres consécutifs Somme des entiers, des carrés… Somme et produit – Trouver les deux nombres Tautochronie Théorèmes
Site	A Collection of Algebraic Identities – Tito Piezas
Cette page	http://villemin.gerard.free.fr/Wwwgvmm/Identite/Ident.htm

Continuité de liens:

Identité degré 5 transférée