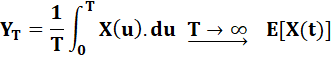En bref
|
Un
processus est ergodique lorsque la variation
d'un seul processus au cours d'une période de temps est semblable à celle de
beaucoup de processus simultanés. Exemple:
la croissance des arbres est ergodique si on peut anticiper la croissance
d'un arbre au cours du temps en observant simultanément l'ensemble de la
forêt. |
|
Approches |
Les chaussures J'en achète une très grande quantité qui me plaisent en une fois ou je
les achète une par une chaque jour. Si le résultat est le même, le système
est ergodique. L'explorateur Parmi la foule de gens, il y a des explorateurs. À force d'explorer,
chacun aura suivi sa propre trajectoire, et sur un temps infini, ils auront
tous tout vu. Mais qui sait? Certains sont peut-être prisonniers quelque
part. Ergodique ou pas? Les dés Si vous lancez 1000 dés ou si vous en lancez un
seul 1000 fois, vous obtenez les mêmes résultats statistiques si les dés ne
sont pas truqués et si les lancés sont indépendants les uns des autres. Très bien, le système est ergodique! Mais l'ergodicité s'intéresse aussi à des
scénarios plus complexes. Imaginons qu'il existe une corrélation temporelle
entre les différents lancés. Que se passe-t-il? À quelle vitesse la
statistique de ces lancés va converger vers la statistique initiale, celle
sans corrélation? C'est le style de question que se pose la théorie
ergodique. Les molécules L'hypothèse d'ergodicité revient à dire que
l'on peut mesurer la vitesse moyenne des particules de deux façons
équivalentes:
Les hommes Il n'est pas possible de donner la taille moyenne des hommes actuels
en observant les statistiques sur les générations précédentes. La croissance
humaine n'est pas ergodique. La cuve de gaz Deux compartiments: l'un vide et l'autre rempli de gaz. On ouvre la
séparation entre les deux compartiments. La théorie ergodique prédit ce qui
va se passer. Le point de départ de la
théorie ergodique provient du développement de la mécanique statistique et de
la théorie cinétique des gaz, où l’expérience suggère une tendance à
l’uniformité: si l’on considère à un instant donné un mélange hétérogène de
plusieurs gaz, l’évolution du mélange au cours du temps tend à le rendre
homogène.” J. Dieudonné – 1977. |
|
Intérêt |
La théorie ergodique Elle traite des systèmes dynamiques et de leur
comportement en moyenne. De nombreux systèmes sont connus pour être chaotiques. Il est impossible de
prévoir leur comportement du fait du manque de précisions (ultra-précises)
sur leurs conditions initiales. Alors, la théorie ergodique est mise en œuvre
pour tenter de faire des prédictions tout de même. La conjecture de Syracuse Transformation qui envoie un nombre n vers sa moitié
s'il est pair et vers trois fois sa valeur plus un, sinon. Le comportement de
cette suite de nombres semble aléatoire et inexplicable. Est-il ergodique? En
tout cas, c'est une piste d'analyse exploitée par les mathématiciens >>> |
![]()
|
Transformations |
La transformation du boulanger est
un bon exemple pour apprécier le sujet d'étude de la théorie ergodique. En itérant un grand nombre de fois la
transformation du boulanger, on observe que les points d’une partie A donnée
au départ semblent se répartir uniformément dans tout le carré :
|
|
Récurrence |
Les
cartes de Poincaré: la probabilité
pour qu’après un battage assez long une carte occupe une
place donnée est indépendante de la position qu’elle occupait initialement. C’est parce
qu’ils admettent cette ergodicité que les joueurs
font confiance au battage (sans tricherie) des cartes pour rétablir une
situation de hasard avant de commencer une nouvelle partie. Théorème
de récurrence de Poincaré: Presque tous les
points d'un sous-ensemble de l'espace finiront par repasser là où ils étaient
dans leur état initial. Plus
rigoureusement: pour presque toutes les conditions initiales, un système dynamique
(…) fini va repasser au cours du temps aussi près que l'on veut de sa
condition initiale, et cela de façon répétée. |
|
En gros |
Théorie ergodique: vous avez un espace et une transformation que vous
appliquez sans cesse. La question est de savoir si l'espace va devenir en
quelque sorte homogène selon une définition à préciser. |
![]()
|
Ergodique |
Définition (CNTRL) Hypothèse, postulat, principe, théorie ergodique:
qui permet de déterminer statistiquement toutes les réalisations d'un
processus aléatoire à partir d'une réalisation isolée de ce processus. Physique statistique Étude du comportement d'un système dynamique sur une
longue période de temps. L'hypothèse ergodique est vérifiée si elle permet
de faire des prédictions correctes. Rapprochement entre la théorie et l'expérience. Loi de la généralisation Comment inférer une généralisation à partir d'un
certains nombres de faits, d'expérimentation? Si le système est ergodique
alors la généralisation a de grandes chances d'être correcte. Processus ergodique C'est un processus stochastique (aléatoie) pour lequel les statistiques peuvent être
approchées par l'étude d'une seule réalisation suffisamment longue. |
|
Maths |
On dit qu'un processus aléatoire stationnaire
X(t) est ergodique au premier ordre si:
À gauche, une intégrale
qui témoigne d'une analyse sur la longueur du temps et à droite une moyenne
exprimant une vision globale instantanée. Voir Équations de Lorenz Une explication raccourcie: La théorie ergodique prouve que la moyenne sur le
temps est égale à la moyenne sur l'espace. |
![]()
|
Historique |
En 1871, Ludwig Boltzmann formule l'hypothèse
ergodique pour les besoins de sa théorie cinétique des gaz (grand nombre de particules). Elle affirme qu'à l'équilibre, la valeur moyenne
d'une grandeur calculée de manière statistique est égale à la moyenne d'un
très grand nombre de mesures prises dans le temps. 1880: Maxwell formule également cette hypothèse. 1900: Poincaré – Théorème de la récurrence. 1931: von Neumann –
Théorème de la moyenne ergodique. 1931: Birkhoff – théorème ergodique individuel. 1958: Kolmogorov – Entropie comme invariant. 1963: Sinai – Le flux
du billard est ergodique. |
|
Français |
Du grec ergon: travail,
énergie et hodos: chemin, route, moyen. |
|
Anglais |
Ergodic hypothesis. Baker's map : transformation du
boulanger. Mapping: application
(ou fonction), relation entre deux ensembles pour laquelle chaque élément du
premier (appelé ensemble de départ ou source) est relié à un unique élément
du second (l’ensemble d'arrivée ou but). One way of studying the
behavior of a system is to take a time average of the system variables. An alternative is to
imaging creating a large number of replicas of the system such that all
possible states of the system are present in abundance. The ergodic
hypothesis then asserts that averaging over this collection (ensemble) of
replicas gives the same result as taking a time average. It is particularly
used in statistical thermodynamics. |
![]()
|
En savoir plus |
|
|
Sites |
|
![]()