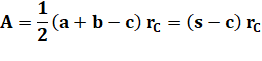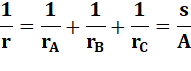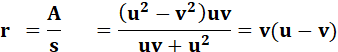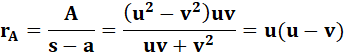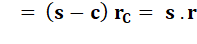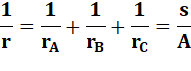|
||||||||||||||||||||||||||||||||||||||||
![]()
|
CERCLES EXINSCRITS Ils sont trois
pour tout triangle. Les trois centres sont les
sommets du triangle
exinscrit. Les trois cercles exinscrits
et le cercle inscrit répondent au problème n°3
d'Apollonius: Cercles tangents à trois droites (DDD ou LLL) |
Voir Définitions
des trois types de cercles
|
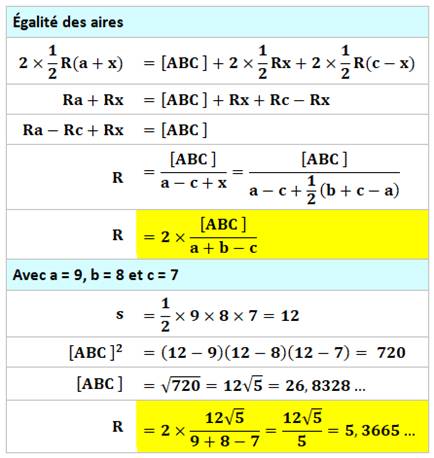
La résolution n’est pas simple. Elle exploite la longueur égale des segments
de tangente et un calcul des aires de triangle. La formule
de Héron est en action. |
||
|
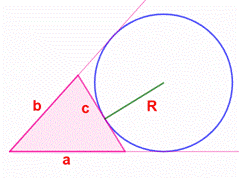
Construction Un
triangle quelconque et un de ses cercles exinscrits. Calculer
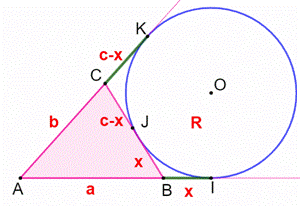
le rayon de ce cercle en fonction des trois côtés du triangle. Piste (Figure du milieu) Le cercle
est tangent aux côtés du triangle, dont deux sont prolongés. Les points I, J
et K sont les points de tangentes. On
identifie deux paires de segments de tangences de mêmes longueurs notées x et
c – x sur la figure. La
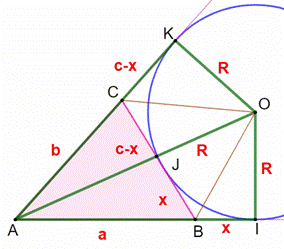
troisième paire (AI, AK) donne ; Aires des triangles (Figure du bas) On évalue
l’aire du
quadrilatère AIOK de deux manières : Évaluation [ABC] = aire du
triangle ABC
|
Figure initiale
Figure avec notation
Identification des triangles
|
|
Voir Calcul du rayon dans le cas
d'un triangle isocèle
|
|
|||
|
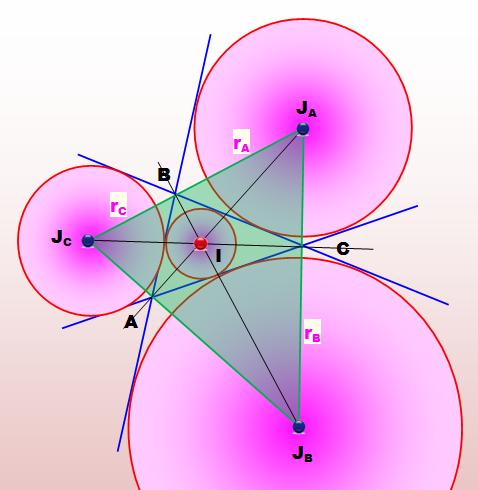
Le
triangle ABC et le prolongement de ses côtés (bleu). Les
quatre cercles sont tangents à trois côtés internes ou externes. Le cercle
inscrit a pour centre I et les trois exinscrits JA, JB
et JC. Ces trois points forment le triangle exinscrit. Les
droites qui les joignent sont les bissectrices des angles intérieurs et
extérieurs. |
|
||
|
Par comparaison des aires, un calcul conduit à
l'expression du rayon des cercles exinscrits. |
avec s = ½ (a
+ b + c) |
||
|
Avec les
deux autres cas et celui du cercle inscrit. La valeur
de l'aire peut être calculée avec la formule
de Héron. |
|
||
|
Un peu de
calcul permet de calculer: |
|
||
|
Relations
entre les rayons: |
|
||
|
|
||
|
Caractérisation
des côtés du triangle (triplet
de Pythagore). |
a = u² – v², b = 2uv, c = u² + v² Avec u > v, des nombres
entiers |
|
|
Aire: |
A = ½ (u² – v²) 2uv = uv (u – v) (u +
v) |
|
|
Rayons
(calculs faits): avec
s = ½ (a + b + c) |
|
|
|
Les
nombres u et v étant entiers (u > v), les rayons sont des nombres entiers
positifs. |
Théorème La longueur du rayon des cercles exinscrits dans un triangle de
Pythagore sont des nombres entiers. C'est le cas
aussi pour le rayon du cercle inscrit, mais
pas pour le circonscrit. |
|
|
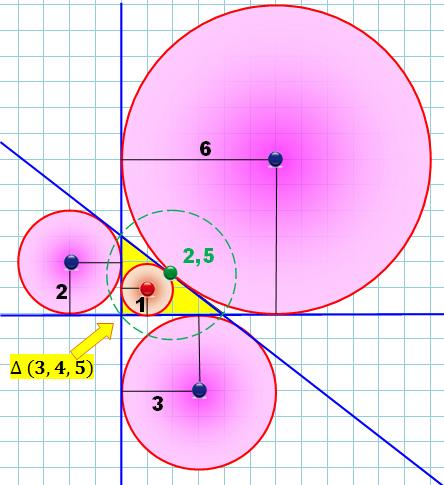
Cas du triangle (3, 4, 5) avec u =
2 et v = 1 Voir figure Les
rayons sont alors:
Cas du triangle (5, 12, 13) avec u =
3 et v = 2 Les
rayons sont alors:
|
|
|
|
|
||
|
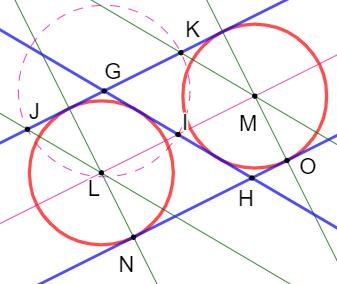
But Construire les deux cercles rouges tangents aux
trois droites bleues dont deux sont parallèles. Construction Point I milieu de GH. Parallèle en I aux droites bleues. Cercle (G, GI). Intersections J et K. Parallèles en J et K à la droite bleue sécante. Intersections L et M. Perpendiculaires en L et M à une des droites
parallèles. Intersections N et O Cercles (L, LN) et (M, MO) qui sont les deux
cercles cherchés (rouges). |
|
|
![]()
|
Suite |
|
|
Voir |
|
|
Site |
|
|
Cette page |
![]()