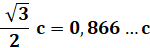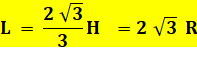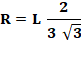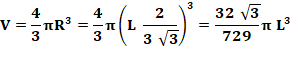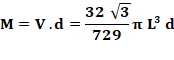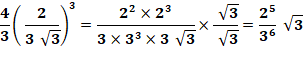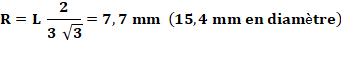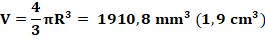![]()
|
|
Ce site est désormais accessible en http://diconombre.fr/index.html et
pour cette page voir le lien en fin de page |
|
22 Novembre 2025
![]()
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Pages sur le triangle équilatéral
|
Équilatéral
(1/3) |
Équilatéral
(2/3) |
Équilatéral
(3/3) |
![]()
|
Propriétés générales en première partie. Propriétés spécifiques en deuxième partie. Théorème de Viviani en troisième partie. Figure avec triangles équilatéraux >>> (Logo de la société américaine Vectornav – Systèmes de navigation)
|
|
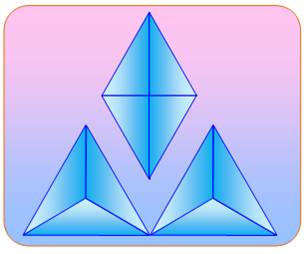
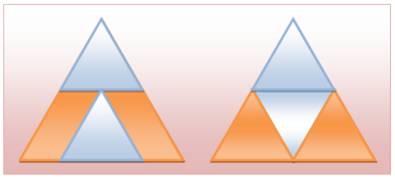
Un
grand triangle équilatéral et deux petits identiques disposés l'un sous
l'autre. Que peut-on dire de l'aire
des deux parallélogrammes marron?
|
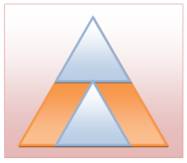
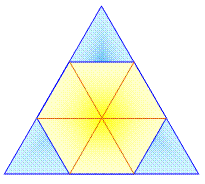
Un
hexagone est inscrit dans un triangle équilatéral. Quelle
est l'aire de cet hexagone?
|
|
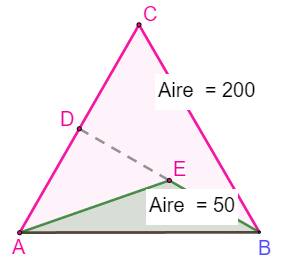
Problème ABC
est un triangle équilatéral. Le point D est le milieu de AC, et E celui de
DB. Montrer
que l'aire du triangle ABE est le quart de celle du traiangle équilatéral. Solution Aire
AEC = 1/2 AC x DE = 1/2 Aire de ABC Aire
AECB (complémentaire) = 1/2 Aire de
ABC. Les
triangles AEB et CEB sont égaux (congruents). Aire
AEB = 1/4 Aire de ABC. |
|
|
|
|
Triangle dont les trois côtés sont
égaux (de même longueur).
|
|
Autres noms: triangle équiangle ou triangle
isoplure (Renaissance)
|
|
||
|
Triangles équilatéraux
en situation
|
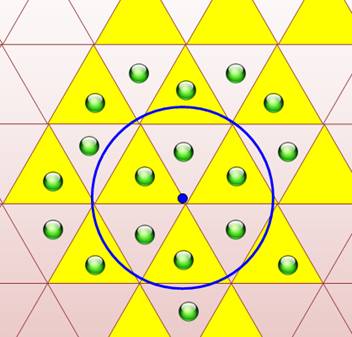
Un pavage de triangles
équilatéraux et un cercle de rayon égal au côté des triangles
Le
cercle englobe et
touche au maximum 18
triangles équilatéraux |
|
Voir Pavage
du disque
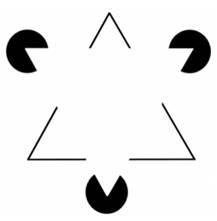
Triangles équilatéraux jumeaux qui jouent à
cache-cache
|
|
||
|
|
|
|
Voir Polygones et calcul de
Pi / Nombre
0,866 …
|
|
|||
|
Nom |
Triangle
équilatéral |
|
|
|
Famille |
Polygone à 3
côtés |
||
|
Sommets |
3 |
||
|
Côtés |
Trois côtés égaux
(isométriques) |
||
|
Périmètre |
3c |
||
|
Angles |
60 ° soit |
||
|
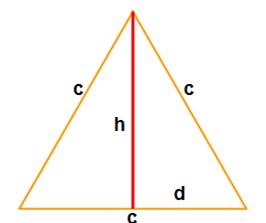
Hauteur |
|
||
|
Aire |
Voir
Nombre 0,433… |
||
|
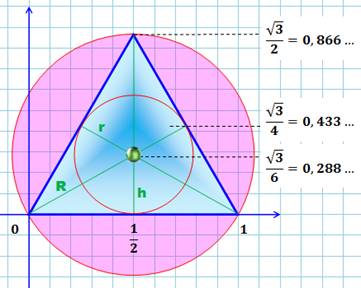
Cercle inscrit et circonscrit |
|
Aire du cercle circonscrit /
aire du cercle inscrit = 4; l'aire de la couronne (rose) vaut trois fois
celle du cercle inscrit. Voir
Propriété amusante sur cette
figure |
|
|
Propriétés |
Les droites caractéristiques
issues d'un même sommet sont confondues: Hauteurs, Médiatrices, Bissectrices. Elles ont le même
point de concours: Orthocentre, Centre du cercle
inscrit, Centre du cercle
exinscrit. Ce point est
situé au 2/3 de
distance à partir du sommet:
Elles constituent
trois axes de symétrie
du triangle. |
||
Voir Construction de
l'heptagone
Le saviez-vous? Le nombre 1/3 se cache dans le triangle
équilatéral
|
Cette
simple construction avec deux triangles équilatéraux permet de trouver un des
points situé au 1/3 du segment bleu. |
|
|
|
|||
|
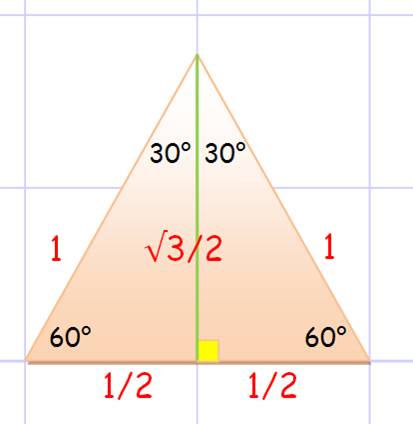
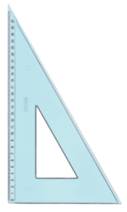
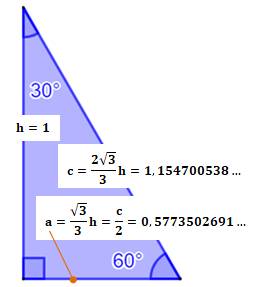
Certaines équerres sont en forme de
demi-triangle équilatéral; en fait un triangle
rectangle. Les angles à la base valent 30° et
60°. |
|
30° 60° |
|
|
|
||
|
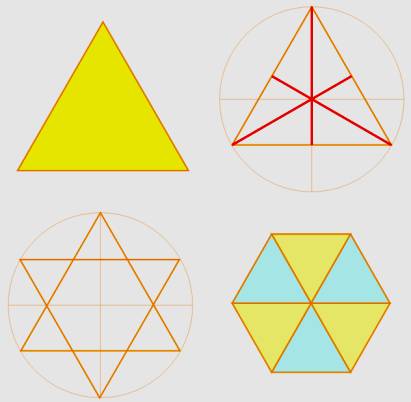
Il existe six déplacements qui
laissent le triangle équilatéral identique à lui-même. |
|
|
|
|
|
|
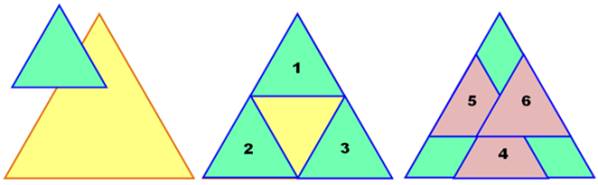
Un triangle équilatéral (jaune) et son clone quatre fois plus petit (vert).
Combien de petits triangles au minimum pour recouvrir complètement le grand.
Seuls les glissements son autorisés, pas de rotation. Solution Première idée: placer trois
triangles dans les angles et en mettre un quatrième au centre. Contraire à la
demande, il ne faut pas les retourner. Il faut trois autres triangles
(roses) pour couvrir le trou central.
|
|
|
|
|
|
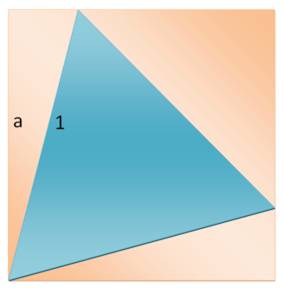
Un triangle équilatéral de côté unité et un carré de côté a. Quelle est la valeur minimale de a pour y inscrire le triangle équilatéral?
|
|
Voie
Site:
Triangles équilatéraux
dans carré (amusement)
|
|
|
|
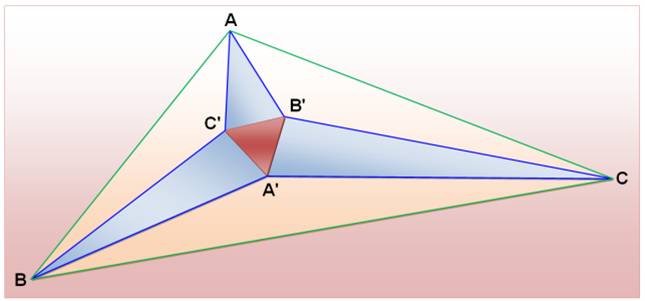
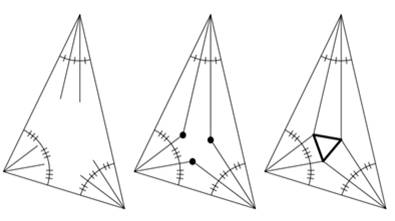
Il existe au moins un triangle équilatéral dans chaque
triangle quelconque. Il se niche à l'intersection des trisectrices. Frank Morley (1860-1937),
mathématicien anglais qui a enseigné aux États-Unis. Théorème de Morley
(1899) Les points
d'intersection des paires de trisectrices adjacentes des angles d'un triangle
sont les sommets d'un triangle équilatéral.
Les trisectrices extérieures sous-tendent également des
triangles équilatéraux. En comptant bien, il est possible de révéler 27 triangles
équilatéraux! Rappel: Trisectrice en A => les
angles BAC', C'AB' et B'AC sont égaux (isométriques) Construction
|
|
|
Voir
Démonstration
en Le
théorème de Frank Morley de Thérèse Eveilleau Voir
Démonstrations
en Théorème
de Frank Morley d'Abracadabri Voir
Démonstration
visuelle de Conway (animation) Voir Morley's Miracle – Cut-the-Knot – Alexander Bogomolny - (13 preuves) Voir
Trisection du segment
avec des triangles équilatéraux |
|
|
|
||
|
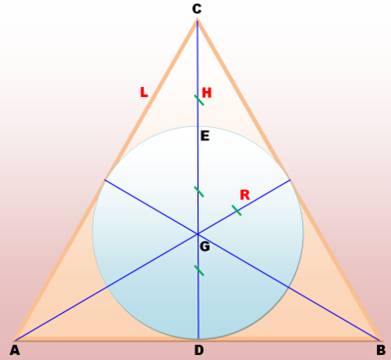
Le centre du cercle inscrit est aussi le centre de gravité
du triangle équilatéral. R = GE = GD Or le point G est au deux
tiers de la médiane CD. GD = CD/3 Bilan: R = GE = GD = CE H = 3R
L = 1,1547… H = 3,4641… R La droite médiane, hauteur et médiatrice d'un triangle
équilatéral est partagée en trois parties égales par le cercle inscrit et
chacune est égale au rayon du cercle. |
|
|
|
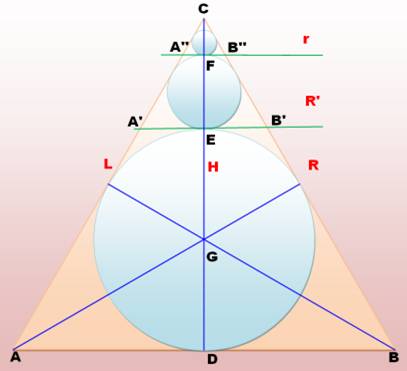
Application Quelle est la taille L du triangle
équilatéral ABC en fonction du rayon r du petit cercle? Il s'agit de l'application
de la propriété indiquée ci-dessus aux trois triangles équilatéraux: ABC,
A'B'C et A''B''C.
|
|
|
Voir Cercles inscrits dans le triangle
équilatéral
|
Application en usinage Avec un foret d’usinage mécanique ordinaire (angle de la pointe à
60°), on perce un trou conique dans une pièce en métal, le trou ainsi fait
est capable de recevoir une bille en acier de telle façon qu’elle affleure la
surface de la pièce. On demande quel est le poids de la bille sachant que la densité de
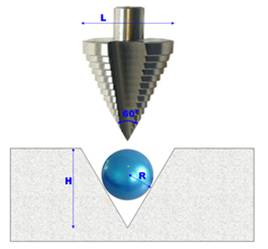
l'acier de la bille est de d = 2,45. Solution La figure montre que la
bille est logée telle qu'une section soit inscrite dans un triangle
équilatéral. Son rayon est lié au diamètre de taille L (côté du triangle) par
la relation:
Volume de la sphère:
Masse de la bille
|
Foret, pièce métallique usinée et bille dans le
trou conique
Note: calcul du coefficient
Exemple numérique avec un foret de 20 mm
|
Triangle
équilatéral en plein exercice artistique
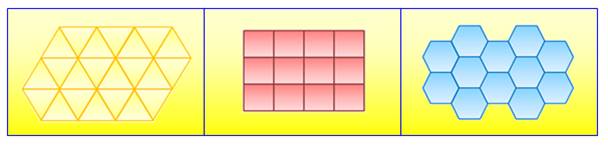
Les trois
seuls pavages réguliers du plan
|
Le triangle équilatéral est
impliqué dans un des pavages réguliers et dans six des pavages semi-régulier
du plan.
|
Voir Pavage du plan
|
Solution en image:
il suffit de retourner le petit triangle
équilatéral du bas pour se rendre compte que chaque parallélogramme occupe la
place d'un petit triangle équilatéral (1/4 de l'aire du grand).
Sinon: la hauteur du grand triangle est
le double de celle du petit. Les côtés sont également dans un rapport 2. Les
deux triangles bleus occupent la moitié de l'aire du grand. Reste une moitié
pour les deux parallélogrammes identiques: soit 1/4 du grand pour chacun; la
même aire que pour chaque petit triangle. Pourquoi 1/4:
|
|
Solution
avec le tracé des diagonales de l'hexagone: H = 6t (aire de l'hexagone égal
six fois l'aire du petit triangle équilatéral). Aire du grand
triangle: T = 9t Aire de l'hexagone =
2/3 de celle du triangle. Pourquoi ça marche? En posant
l'hexagone sur la base du triangle, le côté haut est parallèle à la base et
le petit triangle du haut est équilatéral. Ses côtés sont égaux au côté de
l'hexagone. Idem pour les deux autres petits triangles. Le côté du grand
triangle est bien découpé en trois segments de même mesure. |
![]()
![]()