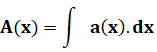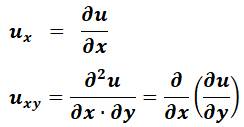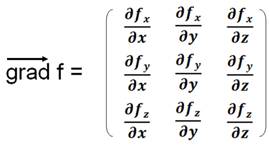Voir DicoMot Math:
différentiel
|
Approche |
10 km +
0,5h x 50 km/h = 10 km + 25 km = 35 km
40 km +
2 x V = 100
x + 2 x V = 100
Avec
|
|
Remarques |
|
|
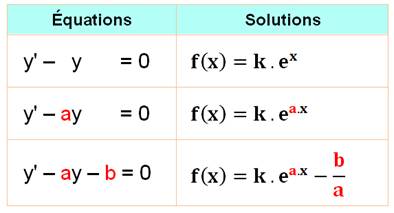
Équations classiques |
ax² + bx +
c = 0.
ax² + bx +c + px-2 = 0 ax² + bx + c + px1/2 = 0 Note: j'ai introduit la constante "p" plutôt
que "d" pour ne pas créer de confusion avec le "d" de la
dérivée. |
|
Définition des équations
différentielles |
Note: ici "dx" comme "dt "forme un bloc inséparable qui
veut dire "une petite partie de x" ou "une petite partie de
t". Pour les plus avancés en maths, on trouvera aussi
|
Résumé
des notations les plus correctes
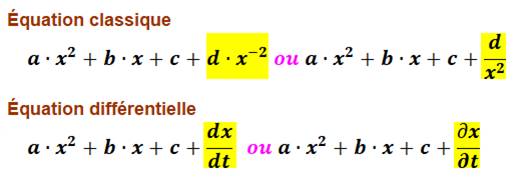
Merci à Jean Florent pour ses remarques
|
Vocabulaire |
|
|
Exemples |
La constante réelle C est déterminée par la
connaissance d'une valeur de y0 pour x0. Exemple: y' = cos
(t)
|
![]()
|
Un exemple pourtant simple! Une
idée de la complexité de la résolution |
|
y' + a(x) . y = 0 ou |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a = sin (x)
|
![]()
Exemple
d'applications
|
g étant l'intensité de la pesanteur.
Équation non linéaire du fait de la présence de
v². |
|
|
Le pendule |
et la solution est évidemment plus simple à
trouver. |
|
Ressort |
|
|
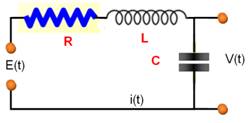
Circuit |
|
![]()
|
Équations aux dérivées
partielles EDP |
|
|
Notations |
Exemples
|
|
Abréviations |
Exemples ci-dessous pour un espace en 3D (x, y et z). |
|
Forme différentielle |
|
|
Nabla |
|
|
Gradient |
|
|
Divergence |
|
|
Laplacien |
|
|
Rotationnel |
|
|
Hamiltonien |
|
|
D'alembertien |
|
![]()
|
|
|
|
Équations différentielles |
|
|
Autres |
![]()