|
Édition du: 21/11/2024 |
|
INDEX |
ELLIPSES |
|||
![]()
|
Ellipse – Constructions Comment dessiner
une ellipse, ses foyers et ses directrices ? |
||
|
|
Sommaire de cette page >>> Cercle et ellipse – Construction du jardinier >>> Une ellipse sympathique >>> Construction des foyers >>> Construction de la directrice >>> Construction de la tangente >>> Construction de l'ellipse – Méthode oblong >>> Construction avec cercles concentriques >>> Construction avec ellipsographe >>> Ellipse inscrite dans un triangle |
Débutants Glossaire |
|
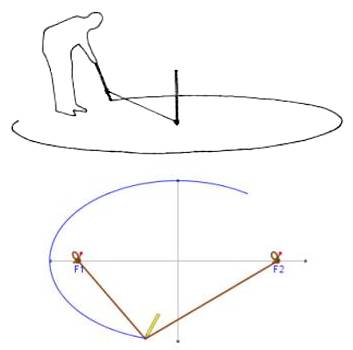
Construction du CERCLE Pour tracer un cercle
au sol en ayant accès au
centre, il suffit de planter un piquet au centre, de tendre une
ficelle de longueur égale au rayon souhaité. Avec un plantoir, un clou ou une craie, marquer
le sol en tournant autour du piquet, ficelle bien tendue. Construction de
l'ELLIPSE Pour tracer une ellipse
au sol en ayant accès
aux deux foyers, planter deux piquets aux foyers et tendre une corde
fixée à ces deux piquets. Avec un clou ou une craie, tendre la ficelle et
marquer le sol en tournant autour des piquets, ficelle bien tendue. Voir Ellipse |
|
|
Voir Constructions
cercle et ellipse / Constructions
géométriques – Index
|
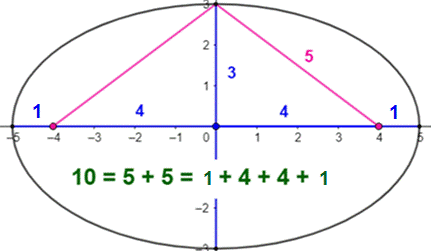
Effet du triangle (3,
4, 5) Ellipse de demi-axes: a = 5 et b =
3. Les foyers sont alors à l'abscisse 4
et -4. Explication Dans le cas particulier d'un point
situé sur le sommet haut, la propriété des distances aux foyers doit être
respectée: Somme pour les traits roses (5 + 5 =
10) doit égaler le grand axe (1 + 4 + 4 + 1 = 10). Ce qui est bien le cas. |
|
|
Voir Triangle
rectangle (3, 4, 5)
Merci à Guy Hekimian pour ses remarques
|
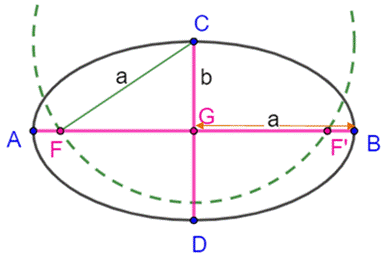
On a le dessin de l'ellipse (en
noir). Les axes AB et CD. On veut tracer les foyers F et F' Construction Cercle de centre C et de rayon a, le
demi grand axe (AB / 2). Intersection en F et F' avec le
grand axe. |
|
|
|
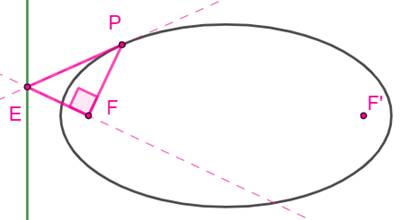
On a le dessin de l'ellipse (en
noir). On veut tracer la directrice (en
vert). Construction Prendre un point P sur l'ellipse. La tangente au point P La perpendiculaire en F à PF. L'intersection E est sur la
directrice. La directrice est la perpendiculaire
au grand axe en E. |
|
|
|
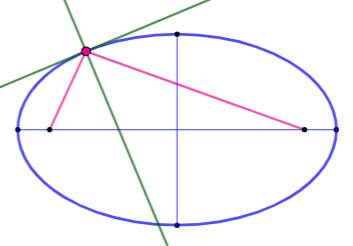
Une ellipse et ses foyers Construction Un point P et les segments qui le
relient aux foyers. Bissectrice de l'angle formé: c'est
la normale. Perpendiculaire: c'est la tangente. |
|
|
|
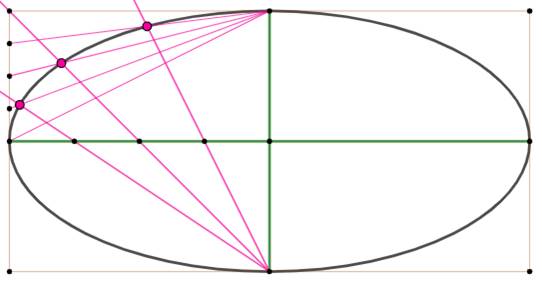
Construction Dessiner les axes souhaités (en
vert). Partager les demi-axes en k parts
(ici k = 4). Réaliser le treillis des doites
issues des deux sommets du petit axe vers les marques de partage. Les points d'intersection
appartiennent à l'ellipse. |
|
|
|
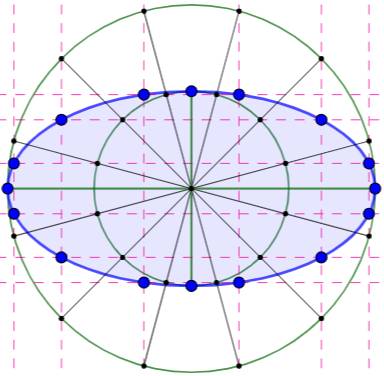
Construction Dessiner les axes souhaités (en
vert). Deux cercles avec pour diamètre la
longueur de ces deux segments. Partage du grand cercle en k parties
(ici k = 12). Diamètres issus des points de
partage et intersections avec le petit cercle. Verticales passant par les points de
partage du grand cercle et horizontales pour ceux du petit cercle. Intersections = points de l'ellipse. |
|
|
|
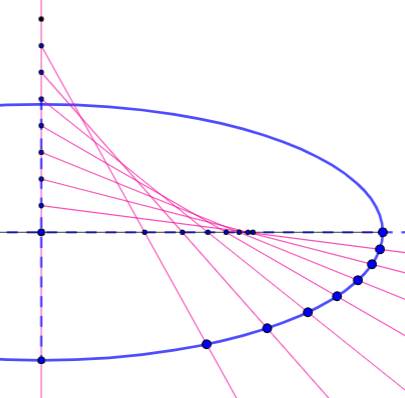
Construction Droite verticale et horizontale. Choisir k points équidistants sur l'axe
vertical à partir du centre (ici k = 8). Choisir une première longueur qui
sera maintenue constante pour construire les rayons joignant l'axe vertical à
l'axe horizontal. Les points sur l'axe horizontal sont irréguliers, c'est
normal. Choisir une seconde longueur qui
sera maintenue constante pour construire les points de l'ellipse sur chacun
des rayons Méthode laborieuse à la main, mais
facilement réalisable avec un outil appelé ellipsographe (ou trammel). Utile pour
les menuisiers et autres artisans. |
|
|
|
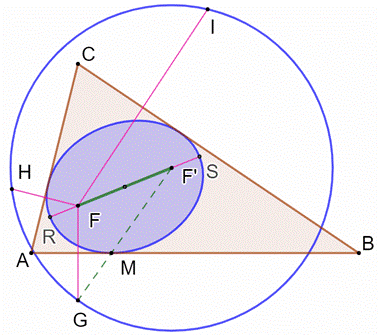
Ellipse Construire une ellipse inscrite dans
le triangle quelconque ABC, étant donné l'un des foyers F (un point
quelconque interne au triangle). Notez que selon la position du foyer
F, il y a une infinité d’ellipses inscrites dans le triangle ABC. Construction Construire les points G, H et I qui
sont les points symétriques du point F par rapport aux côtés du triangle. Le cercle passant par ces trois
points et le cercle directeur de l'ellipse
avec son centre F' qui est le second foyer. Joindre ce foyer F' à l'un des
points du cercle, disons G. Intersection en M avec AB. Construire l'ellipse avec pour
foyers F et F' et passant par le point M. Les logiciels de dessin comme GeoGebra savent réaliser ce type de
tracé. Sinon tracer le lieu des points tels que MF + MF' = RS = F'G = R =
constante. Notez que : FM = MG. |
Ellipse de foyer F
inscrite dans le triangle ABC
Propriété Le cercle
directeur de l'ellipse de foyers FF' a pour rayon le grand axe RS de
l'ellipse. Ce cercle est centré soit sur F soit sur F'. Les points symétriques de l'un des
foyers sont sur le cercle directeur centré sur l'autre foyer.
|
|
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Site |
|
|
Cette page |
http://villemin.gerard.free.fr/Geometri/Coniques/EllipseC.htm
|