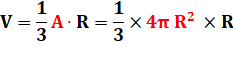|
||||||||||||||||||||||||||||||||
![]()
|
Copie d'élève, citée par Tangente n° 66 –
Avril 2018 |
Voir Pensées & humour
|
SPHÈRE – CALCUL de l'AIRE
et du VOLUME
Voir Valeur de
Pi La sphère prise
pour son volume s'appelle la boule Anglais: surface
area of the sphere, volume of the sphere
Comment
faut-il s'y prendre ? Et la première fois ? Ce n'est effectivement pas
simple. Les mathématiciens anciens procédaient par approximations. Les modernes
ont inventé un outil: le calcul intégral. Voici quatre approches successives ou comment
aboutir au calcul moderne par intégrales:
|
Voir Rubik's
cube
|
|
|||||||
|
Prenons une feuille de papier rectangulaire
ayant les dimensions suivantes: ·
Longueur = diamètre de la sphère, et ·
Largeur = périmètre d'un grand cercle de la sphère La feuille enveloppe complètement la sphère, si
on imagine pouvoir faire les
"découpes nécessaires". |
|
||||||
|
Sa surface (en maths on dit "aire")
est donnée par: |
|
||||||
|
Note |
|
||||||
|
|
|||
|
Principe La circonférence
du cercle, est calculée en encadrant ce cercle par des polygones
dont le nombre de côtés va croissant. Méthode d'exhaustion. |
De la même manière,
l'aire de la sphère est calculée en encadrant cette sphère par des polyèdres: ·
un dedans qui donnera la valeur par
défaut, ·
un dehors qui donnera la valeur par
excès. L'opération est recommencée
avec des polyèdres ayant davantage de faces. ·
Et, ceci, jusqu'à obtenir
l'approximation souhaitée. · Voire
même, en prolongeant à l'infini, la valeur limite donnant l'aire de la
sphère. |
||
|
Faisabilité |
Trouver des polyèdres proches
de la sphère est un problème difficile. On sait facilement inscrire et
circonscrire un cube, ou même un Une tactique consiste
à superposer d'autres polyèdres sur les faces pour s'approcher
progressivement de la sphère. les calculs deviennent vite compliqués. Une autre possibilité
consiste à approximer la sphère par une surface faite de triangles: c'est la
sphère géodésique de Buckminster Fuller. |
||
|
Solutons |
Les solutions retenues
consistent plutôt à sectionner la sphère en tranches (en rondelles de
saucisson ou de salami) ou alors a considérer toutes les pyramides issues de
l'origine. L'astuce consiste à
imaginer des objets avec de très fines épaisseurs pour opérer une
approximation sans conséquence sur le résultat final. Affirmation qui,
aujourd'hui, est confirmée par le calcul formel avec des intégrales. |
||
Voir Calcul du segment de
parabole par exhaustion
|
|
||
|
Le principe du calcul par tranches consiste à
sectionner la sphère en tranches parallèles très fines. Cette méthode s'applique au calcul du volume de la sphère: empilement de
petites tranches de sphères. Elle s'applique aussi au calcul
de l'aire de la sphère: somme des surfaces externes des tranches. Les tranches en question sont, en fait,
légèrement courbes sur leur surface externe. Ces segments de sphère
s'approchent des troncs de cônes La méthode consiste à ramener le calcul sur la
sphère à un calcul sur le cylindre enveloppant. Tranches orange
sur la figure. Nous allons donc étudier ce segment de sphère en
le réduisant le plus possible et en approximant sa partie courbe par une
partie droite. |
|
|
|
Données géométriques du calcul
Notez tout de suite
que le petit triangle bleu est semblable au grand triangle en pointillés:
tous deux rectangles et avec des côtés parallèles qui dessinent des angles
égaux deux à deux. Note plus formelle:
le calcul par tranches tel que le pratiquaient les Anciens produit des
résultats justes. Pourtant, on peut s'interroger sur la légitimité des
approximations qui "deviennent justes" pour des tranches de plus en plus petites.
En analyse moderne, ce doute est levé en introduisant la notion de limite et
en pratiquant un calcul par intégrales. |
||
Anglais: determining volumes by slicing
Voir Calcul avec les
infinitésimaux / Calcul avec intégrales
|
Calcul de l'aire de la
sphère |
|
|||||||||||||||||||||||||
|
Calcul de
l'aire de la sphère A comme somme des aires des segments de sphère Ar. |
|
|||||||||||||||||||||||||
|
Calculs
|
||||||||||||||||||||||||||
Théorème de la boite à chapeau (hat box theorem)
|
The orthogonal
projection from the lateral face of the cylinder onto the sphere is
area-preserving. This of course can be shown by calculus. Remarkably,
Archimedes proved it without using calculus. |
La projection
orthogonale de la face latérale du cylindre sur la sphère préserve la
surface. Bien sûr, cela peut être démontré avec des intégrales. Fait
remarquable, Archimède l'a prouvé sans connaitre l'analyse moderne. |
|
Calcul du volume de la
boule |
|
|
|
Ayant déterminé l'aire, le passage
au volume de la boule est très simple. Imaginons un tout petit carré
(jaune) dessiné sur la surface de la boule, ou toute autre forme polygonale. Formons la pyramide (rouge) ayant ce
carré pour base et le centre de la boule pour sommet. La boule est enveloppée par ces tous
petits carrés qui approximent la surface courbe. |
|
|
|
Volume de la petite pyramide
à base carrée. |
|
|
|
Volume de la sphère = somme du
volume de toutes les pyramides élémentaires formant la boule sphérique
complète. |
|
|
|
La somme des aires de type Acarré
est égale à l'aire de la sphère entière. |
|
|
|
Soit le volume de la sphère: |
|
|
Voir Méthode
d'Archimède avec cylindre et cône / Dérivées
|
La méthode par tranches fines ou celle par découpage en petites pyramides
conduisent aux formules de l'aire et du volume de la sphère. La méthode par exhaustion introduisant le volume
du cylindre et du cône est une autre méthode géométrique >>> Quant au calcul intégral il est
présenté sur une page spéciale >>> |
|
|
||||||
|
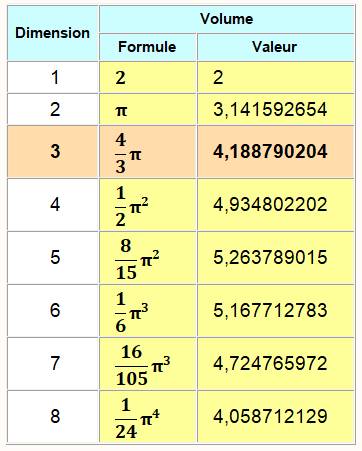
Volume de la sphère selon le nombre de
dimensions du monde considéré => Tableau. Le volume est maximal en dimension 5 puis
diminue ensuite. Sa limite pour une dimension infinie est nulle. En dimension non-entière le volume maximum
correspondrait à:
|
|
|||||
Voir Diconombre
5,25
MERCI A M. Jurkiewicz pour avoir
susciter la révision de cette page
![]()
|
Suite |
· Calcul avec cylindre et cônes · Sphère
– Index |
|
|
Voir |
·
Cercle · Cône,
demi-sphère et cylindre ·
Cube ·
DicoMot · Géométrie – Glossaire ·
Géométrie – Index |
· Jeux et puzzles
– Index ·
Logique – Index |
|
DicoNombre |
·
Nombre
4, 18 … |
·
Nombre
12,56 … |
|
Sites |
·
Spherical
polyhedron (polyèdres sphériques) – Wikipedia ·
Geodesic polyhedron
– Wikipedia ·
Surface Area of a
Sphere – Ask Dr. Math / Rob |
|
|
Cette page |
||
![]()