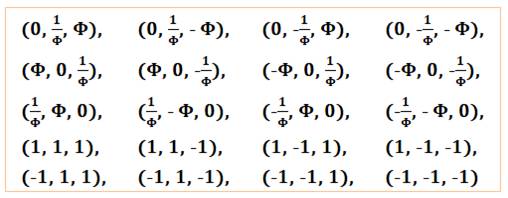|
|||||||||||||||||||||||||||||||||||||||||||||
![]()
|
NOMBRE D'OR & GÉOMÉTRIE Le nombre d'or est
noté Valeur
du nombre d'or:
= 1,618 033 988 749 894 848 204
586 834 365 … |
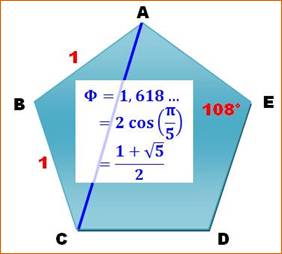
La corde sous 108° est en relation dorée avec le rayon
Le pentagone est le royaume du nombre d'or

|
|
||
|
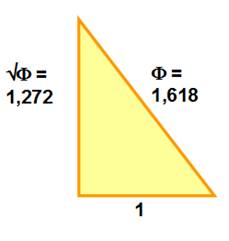
Φ ² = ( En numérique 1,618² = 1,272² + 1 2,618 = 1,
618 + 1 |
Les deux angles: 51,82729234 …° 38,17270766… ° |
|
Voir Triangles isocèles dorés
(Triangles d'or)
|
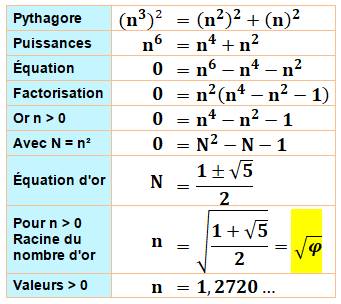
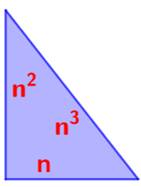
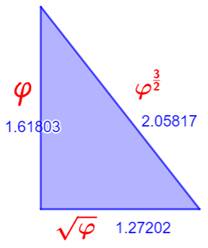
Question Quel
est le seul triangle
rectangle de mesures n, n2 et n3 ? C'est
celui de cette figure dont l'un des côtés est le nombre d'or. Démonstration
|
|
|
Voir Nombre
d'or et son équation
|
|
||
|
|
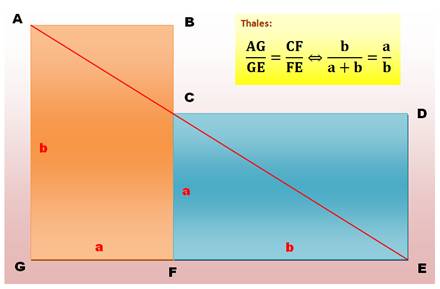
||
|
La relation indiquée sur la figure se traduit par: b² = a² + ab Or b = a a² A n'est pas nul: Qui est l'équation du nombre
d'or. |
|
|
|
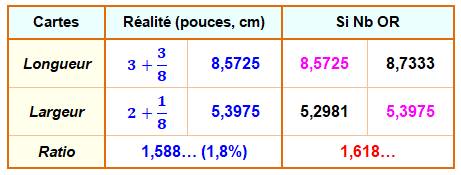
OUI, mais, ce n'est pas exactement un rectangle d'or.
Un écart d'environ 1,8 %. |
Dimensions normalisées (ISO 7810)
des cartes de crédit et dimensions qu'elles devraient avoir pour former un
rectangle d'or parfait.
|
|
Merci à Annie pour ses
précisions et sa vigilance !
|
|
||
|
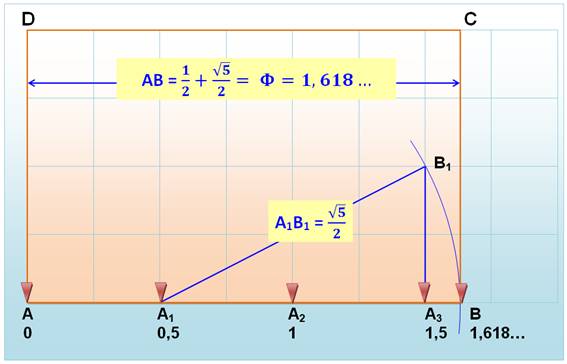
AB
= 1 & BC = Φ
RABCD = Φ
Le
rectangle ECDG est doré: CD
= 1 EC
= Φ – 1 = 1 / Φ R
= 1 / (1/ Φ) = Φ RECDG = Φ
Le
rectangle FJDG est doré RFJDG = Φ |
Successions de
rectangles dorés de plus en plus
petits, jusqu'à
l'infini … Si on ajoute ou retranche un carré au rectangle doré, on forme un nouveau
rectangle doré. Application à
la construction de la spirale, ci-dessous. |
|
|
Relation à noter dans un tel
rectangle
|
||
Voir Rectangles
emboîtés / Rectangle d'or / Construction de Phi
Rectangles d'or (généralisation)
|
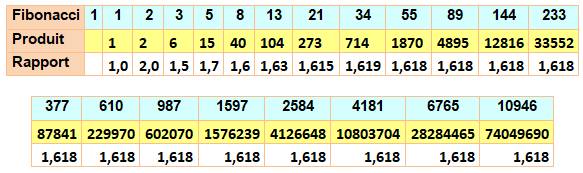
Définition Par extension tous les rectangles ayant pour longueur et largeur deux
nombres de Fibonacci sont appelés rectangle d'or. En effet le rapport de ces
deux dimensions est proche du nombre d'or et tend vers le nombre d'or pour
les plus grandes valeurs. Liste des produits (dimensions des
rectangles d'or)
|
|
|
|
|
Spirale
logarithmique ou équiangulaire
Toutes les lignes
droites partant de son centre coupe la spirale exactement sous le même angle.
|
|
|
|
|
|
Icosaèdre
Octaèdre
Dodécaèdre
on
forme 3 rectangles d'or perpendiculaires
ente eux. |
|
|
|
|||
|
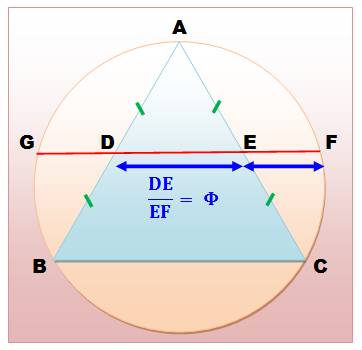
Propriété Un triangle équilatéral ABC
et son cercle circonscrit. Les
points milieux D et E et la droite De qui coupe le cercle en F et G. Alors DE
/ EF = nombre d'or. Démonstration On note
DE = a et EF = b et a / b
= x |
|
||
|
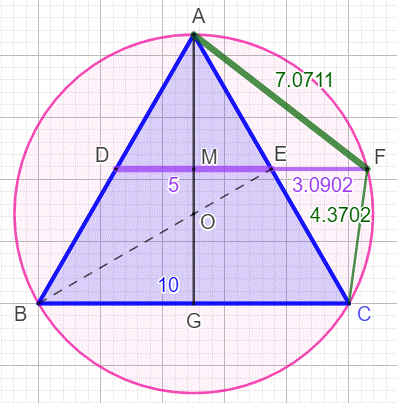
Triangle
équilatéral et points milieux |
AE
= EC = DE = a GD
= EF = b |
||
|
AE
. EC = GE . EF |
|||
|
En
remplaçant |
a
. a = (a + b) b a²
= ab + b² |
||
|
En
divisant par b² et en utilisant x |
x²
= x + 1 dont
la racine est le nombre d'or. |
||
|
Le nombre
d'or se trouve aussi dans le rapport des longueurs AF / FC. Voir Démonstration par J.-L. Breuil |
|
||
Voir Construction du pentagone par Jean-Louis Breuil
|
Dodécaèdre régulier
de côté 2/Phi: coordonnées des 20 sommets
Avec
les centres des 12 pentagones, on forme 3 rectangles d'or
qui se coupent à angle droit au centre. Dodécaèdre
et cube inscrit: coté de l'un sur côté de l'autre = Phi Icosaèdre régulier de
côté 2
Avec
les 12 sommets, on forme 3 rectangles d'or qui se coupent à angle droit au
centre. Cube
et icosaèdre inscrit; coté de l'un sur
côté de l'autre = Phi |
![]()
|
Suite |
|
|
Aussi |
|
|
DicoNombre |
|
|
Site |
|
|
Cette page |
![]()
Renvois de
liens
Ellipse
dorée
Croissant
de lune - lunule
Triangle et
rectangle en or
Pentagone et étoile à 5 branches