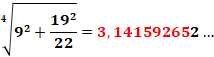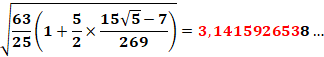|
Édition du: 21/11/2024 |
|
INDEX |
Histoire des maths – Antiquité |
|||
Faites
un double-clic pour un retour en haut de
page
![]()
|
QUADRATURE DU CERCLE Tetragônismos Ou l'impossibilité de dessiner Les Anciens ont cherché à dessiner à la règle et au compas un carré
qui aurait la même aire que le cercle. Ils n'arrivaient qu'à des solutions
approchées sans trouver la bonne. En 1882, Lindemann trouve le fin mot: la
constante Pi est transcendante (décimales diverses sans fin) et la
construction est impossible. En 1925, Tarski propose une nouvelle piste: la dissection. Est-il
possible de composer un carré et un cercle de même aire en utilisant les
mêmes pièces élémentaires. En 2002, après de nombreuses avancées, trois
mathématiciens publient une solution comportant plus de dix mille pièces. |
||
|
|
Sommaire de cette page >>> Carré et
cercle – Périmètre et aire >>> Carré et
cercle – Comparaison >>> Pseudo
quadrature >>> Historique – Recherche de la quadrature >>> Historique – Précurseurs >>> Quadrature du cercle et
transcendance de Pi >>>
Historique – Recherches d'approximations >>>
Historique – Recherches modernes |
Débutants Glossaire |
Anglais: it is
impossible to square the circle by compass and straightedge
|
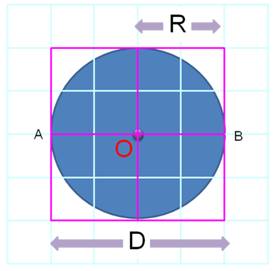
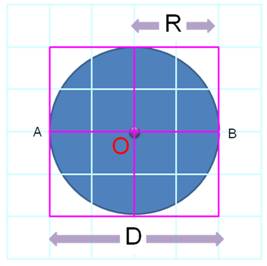
Périmètre du carré = 2 x
4 x R Périmètre du cercle = 2 x 3,14 … x R |
Aire du carré = 4 x R² Aire du disque = 3,14… x R² |
|
Voir Un bon moyen de retenir ces formules (P =
2πR et A = πR²)
|
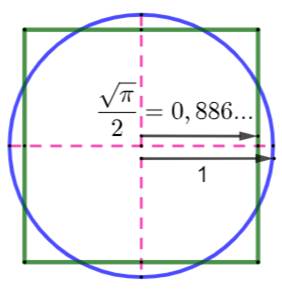
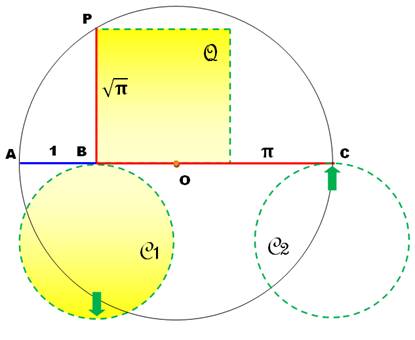
La figure montre
un cercle d'aire unité et le carré de même aira qui aurait un côté de
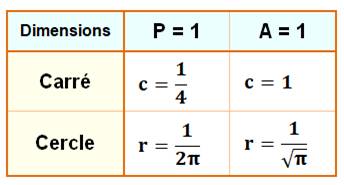
longueur racine de Pi. Quelles sont les
dimensions du carré et du cercle pour un périmètre ou une aire unité ?
|
|
|
|
Cette
construction est basée sur la construction
de la racine d'un nombre. Supposons que
nous sachions construire la longueur Pi = BC Allongeons ce
segment d'une unité AB. Selon sa
construction, la racine de Pi est matérialisée en PB. L'aire du carré
(Q) construit sur PB est égale à Pi. C'est également l'aire du cercle de
rayon unité (C1). Aire du carré Q = Aire du
cercle C1 Reste à
construire la valeur de Pi ! C'est la mesure
d'un demi-périmètre du cercle unité C1 En vert, on
montre comment faire rouler C1 jusqu'en position C2
pour développer la distance Pi = BC. Le problème:
cette opération de roulement n'est pas autorisée. Elle ne correspond pas à la
rigueur des constructions à la règle et au compas. |
Un cercle qui roule
sans glisser de B à C développe un demi-périmètre égal à Pi. La construction de la
racine carrée permet de tracer BP la racine de Pi.
|
|
Voir Tentatives de quadrature du cercle / Construction
brouette
|
Problème |
Construire un carré et un cercle de même périmètre avec règle et compas. Ou de même aire (problème
équivalent). |
|
|
Égyptiens |
Papyrus Rhind – vers 1650 av. J.-C. |
|
|
Anaxagore
de Clazomène (vers 500- 428 av. J.-C.) |
Anaxagore de Clazomène, mathématicien grec, est
en prison pour avoir affirmé que le soleil n'est pas un
dieu, mais plutôt un rocher incandescent aussi grand que la péninsule du
Péloponnèse. Philosophe convaincu que la raison gouverne le monde, il a profité de son incarcération
pour s'attaquer à un problème mathématique désormais célèbre, la quadrature
du cercle: à l'aide d'un compas et d'une règle, comment dessiner un carré de
surface égale à un cercle donné ? Plutarque rapporte cette reherche; mais on ne
connait pas la construction d'Anaxagore. |
|
|
Hippocrate (-470
à -410) |
L'aire de la lunule (ou
lune) d'Hippocrate est
rigoureusement égale à celle d'un triangle. Une telle propriété a longtemps
fait penser que la quadrature du cercle était réalisable. |
|
|
Aristophane
(vers 444 - 380 av. J.-C.) |
Première
indication du problème: "Avec une
règle, je vais donner la forme du carré au cercle". |
|
|
Les
Grecs |
Ils croyaient
avoir trouvé. Il est vrai que leurs résultats étaient de très bonnes
approximations. Ils se sont vite
rendu compte que la résolution était extraordinairement difficile, voire
impossible. |
|
|
Archimède -287
à -212 |
Archimède cherche à
approcher le cercle par encadrement avec des polygones. |
|
|
Francon
de Liège 1050 |
Francon propose une
dissection d'un cercle de diamètre 14 en 44 petits secteurs qu'il assemble en
un rectangle (approximatif) de 11 par 14 . |
|
|
Nicholas
de Cusa (1404-1464) |
Cardinal et
savant renommé, il avance que 3,1423 est la valeur exacte de |
|
|
Joseph
Scalinger (1540-1609) |
Il tente aussi
de résoudre le problème. Dans son ouvrage
Nova Cyclometria (1592), il affirme
pourvoir effectuer la duplication du cube et la trisection de l'angle,
c'est-à-dire construire une racine cubique, à l'aide de la seule règle et du
compas, et il prétend avoir trouvé la valeur du nombre d'Archimède (Pi), ce
qui résolvait la quadrature du cercle. Toutes ses
tentatives seront réfutées par Viète. |
|
|
Thomas
Hobbes (1588-1679) |
Ses tentatives
de quadrature du cercle, cubature de la sphère, duplication du cube (1669)
sont réfutées par John Wallis, au prix de violentes disputes entre les deux
hommes. Voir Sa
construction |
|
|
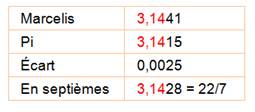
Jacob
Marcelis, |
Il pense avoir
résolu la question. Sa valeur exacte
de
Comparaison
Une bien grande
formule pour si peu de précision ! |
|
|
Edwin
Goodwin en 1897 |
Projet de loi Pi
de l'Indiana. Tentative législative pour établir une vérité mathématique
(erronée, bien sûr): la valeur de Pi, ou plus exactement, le moyen d'obtenir
la quadrature du cercle. On savait
pourtant cela impossible depuis 1882. La présence
accidentelle d'un mathématicien (C.A. Waldo) dans l'Assemblée a heureusement
stoppé le vote et la loi n'a jamais été adoptée. Edwin J. Goodwin
est un médecin et mathématicien amateur. Il pensait avoir découvert une
méthode pour réaliser la quadrature du cercle. Brevet déposé en 1889. Ses
approximations de Pi étaient pourtant très approximatives: de 3,16 à 4 ! |
|
|
Descartes (1596-1650) |
Vers 1630, Descartes prétend
qu'il est parfois possible de prouver l'impossible, notamment en transposant
le problème en algèbre. Il montre que
les nombres constructibles sont un ensemble (corps)
formé des nombres rationnels clos sous l'addition, la soustraction, la
multiplication, la division et la racine carrée. La clôture implique que le
résultat est un membre de l'ensemble. |
|
|
Gauss (1777-1855) |
En 1796, Gauss (19 ans)
réussit à construire un polygone régulier à 17 côtés. Il montre que si
le nombre de côtés n = 2a p·q·r … (p, q, r, … sont des nombres premiers de Fermat),
alors le polygone est constructible. Wantzel montrera
que les nombres premiers doivent être distincts. |
|
|
|
||
|
Fernand von Lindemann |
En 1761, Lambert (1728-1777)
prouve que la constante Pi est irrationnelle, mais ce n'est pas suffisant
pour exclure la construction à la règle et au compas. En 1837, Wantzel (1814-1848)
trouve un critère de non-constructibilité à la règle et au compas appelé
théorème de Wantzel. Une longueur constructible doit être racine d'un
polynôme. En 1873, Hermite (1822-1901)
publie la preuve que la constante e est
transcendantale. C'est après une visite à Hermite que Lindemann a eu l'idée
de sa preuve. Hermite n'était pas loin, mais c'est Lindemann qui a eu la
gloire. En 1882, Lindemann
mathématicien allemand démontre que Pi est transcendant. Pi ne peut
satisfaire aucune équation algébrique à coefficients rationnels (non nuls).
Il n'est qu'une suite infinie de chiffres. Or, un nombre
n'est constructible à la règle et au compas que s'il est solution d'une
équation algébrique, alors la quadrature du cercle est impossible. Publication dans
son article Ûber die Zahl Pi (Au sujet
du nombre Pi). |
||
|
English Corner Lindemann
is famed for his proof that π is transcendental, that is, π is not
the root of any algebraic equation with rational coefficients. The
problem of squaring the circle, namely constructing a square with the same
area as a given circle using ruler and compasses alone, had been one of the
classical problems of Greek mathematics. |
Lindemann
est connu pour avoir apporté la preuve que π est transcendantal,
c'est-à-dire que π n'est pas la racine d'une équation algébrique à
coefficients rationnels. Le
problème de la quadrature du cercle, à savoir la construction d'un carré de
même surface qu'un cercle donné en utilisant uniquement une règle et un
compas, était l'un des problèmes classiques des mathématiques grecques. |
||
Voir
Anglais pour le bac et pour les affaires
|
Ramanujan (vers 1900) |
Il a trouvé une
construction à 6 décimales de Pi correctes en construisant la fraction
366/113. Puis, une autre
avec 8 décimales correcte avec:
|
|
|
Dixon 1991 |
Méthode correcte
avec seulement 3 décimales, mais présentant un bon compromis
justesse-simplicité. Sa formule:
Voir Sa
construction |
|
|
Hùng Viêt Chu 2019 |
Il pousse le
record à 9 décimales à partir des travaux de Dixon qui avait atteint trois
décimales. Sa formule: |
|
Voir Formules approchées de Pi
|
Relance En 1925, Alfred Tarski relance le problème en
modifiant les règles. Il propose de découper le cercle en un nombre
fini de morceaux pouvant être déplacés dans un plan et réassemblés en un
carré de surface égale. Une approche connue sous le nom d'équi-décomposition.
En terme mathématiques: deux objets sont équi-décomposables s'ils peuvent
être divisés en un nombre fini de parties telles que les parties
correspondantes sont congruentes les unes aux
autres. En 1963, il est prouvé qu'un disque ne peut pas
être transformé en aucune autre surface convexe par découpage au ciseaux.
(Lester L. Dubins, Morris Hirsch et Jack Karush, Scissor congruence). |
Faisable ? 1964 – Un article montre que c'est faisable, mais
pas avec des pièces découpées avec des ciseaux; les pièces sont fractales, criblées de
trous et d'arêtes dentelées. 1990, en utilisant la théorie des graphes, Miklós
Laczkovich confirme que le cercle, découpé en 1050 pièces
distinctes, peut être reconfiguré en carré. Il y a un hic ! On ne sait pas
construire les pièces, ni même connaitre leur aire. 2016, Łukasz Grabowski, Máthé et Pikhurko
aboutissent à une preuve presque constructive au détail près qu'il manque une
pièce. Une drôle de pièce qui n'a pas d'aire (un ensemble de mesure zéro). 2017, Marks et Spencer Unger apportent une preuve
qui fonctionne partout, sans exception avec description complète de toutes
les pièces nécessaires à la quadrature du cercle. Leur preuve comporte 10 200
pièces très compliquées, impossible à visualiser. 2022, Andras Máthé
et Oleg Pikhurko de l'université de Warwick et Jonathan Noel de l'université
de Victoria, simplifient la forme des pièces. Il en faut toujours 10
200. |
|
Voir Brève 857
![]()
|
Retour |
|
|
Suite |
Voir Quadrature du carré
|
|
Voir |
|
|
|
|
|
Cette page |
http://villemin.gerard.free.fr/Wwwgvmm/Histoire/Quadcerc.htm |