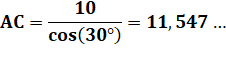|
Édition du: 06/08/2020 |
![]()
|
Angles de 30° et 60° Caractéristiques
de ces angles complémentaires
et constructions.
Lorsqu'on sait construire l'un, on sait construire l'autre. On retrouve ces
angles dans le triangle
équilatéral. Un truc pour couper la tarte en six parts égales. Angle de 60°: sextant. |
||
|
|
Sommaire de cette page >>> Valeurs trigonométriques >>> Construction des angles 30° et 60° >>> Partage de la tarte en six parts égales >>> Construction du triangle équilatéral >>> Angle de 60° passant par un point P externe |
Débutants Glossaire |
Équerre 30-60 (Set square 30-60)

|
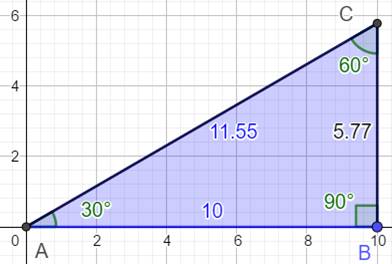
Triangle rectangle (30, 60, 90) AB = 10 (par exemple)
Voir Triangle
30, 60, 90 (triangle de l'écolier) |
|
|
|
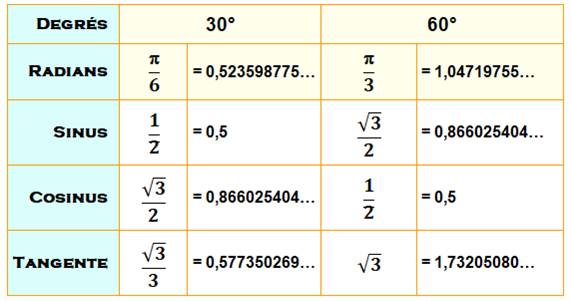
Table des valeurs trigonométriques
|
||
|
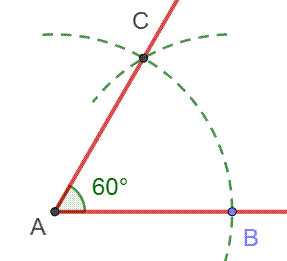
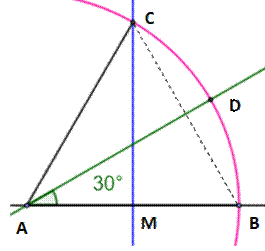
But Construire
l'angle de 60° sur la droite AB avec A comme sommet. Construction
1 – La plus simple pour 60° 1.
Cercle de
centre A et de rayon quelconque. Point B. 2.
Cercle
(B, BA). Intersection C. 3.
Demi-droite
AC. L'angle BAC mesure 60°. Justification Le triangle ABC, avec trois côtés égaux au rayon
des cercles, est équilatéral et chacun de ses angles vaut 60°. |
|
||
|
But Construire
les angles 30° et 60° sur la droite AB avec A comme sommet. Construction
2 1.
Cercle de
centre A et de rayon quelconque. Point B. 2.
Médiatrice
de AB. Intersection en C avec le cercle. L'angle BAC vaut 60°. 3.
Bissectrice
de l'angle BAC. Intersection en D avec le cercle. L'angle BAD vaut 30°. 4.
Variante:
médiatrice de CM qui coupe le cercle en D. Voir Construction facile de l'angle
de 30° |
|
||
|
Couper la tarte
en six parts absolument égales Pas
facile sans repère ! Le truc
est pourtant simple. 1.
Visualiser les traits blancs par la pensée: ligne verticale qui coupe
la tarte en deux, et lignes verticales qui coupent encore en deux 2.
Coupez la tarte selon les traits rouges. Chaque part sera égale à 1/6
de la tarte complète. Voir
Partage de
la tarte |
|
||
|
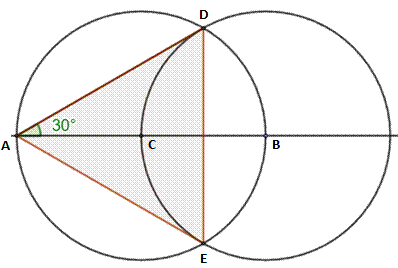
Construction 3
(construction du triangle équilatéral ADE) 1.
On donne le point A sur la droite horizontale 2.
Point C quelconque la droite 3.
Cercle (C, CA). Intersection en B avec la droite 4.
Cercle (B, BC). Intersections en D et E. 5.
L'angle DAE mesure 60° et l'angle DAB fait 30°. |
|
||
|
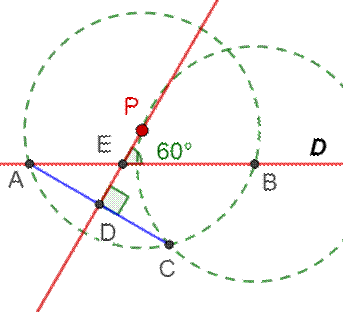
On donne
la droite D et le point P. Construire
une droite passant par P et faisant un angle de 60° avec D. Construction 1 1.
Cercle (P, PA) avec PA de longueur quelconque. Intersections A et B. 2.
Cercle (B, BP). Intersection C. 3.
Médiatrice du segment AC. Elle passe par P et forme un angle de 60°
avec D. Justification La médiatrice de la corde AC passe bien par le
centre P du cercle. Le triangle PBC, avec ses côtés égaux au rayon,
est équilatéral. Angle en P = 60°. |
|
||
|
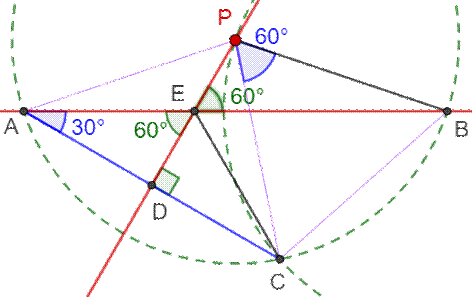
L'angle BAC, inscrit dans le cercle, intercepte
le même arc que l'angle au centre BPC. Il vaut sa moitié: Angle en A = 30°. Le triangle AEC, avec E sur la médiatrice de AC,
est isocèle. Angles en A et en C = 30° et angle en E = 120°. Sa moitié, AED vaut 60°, ainsi que PEB, construit
sur les mêmes droites. |
|
||
|
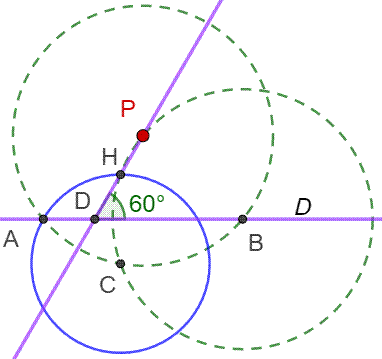
Même
problème: Construire
une droite passant par P et faisant un angle de 60° avec D. Construction 2 1.
Cercle (P, PA) avec PA de longueur quelconque. Intersections A et B. 2.
Cercle (B, BP). Intersection C. 3.
Cercle (C, CA). Intersection H. La droite passant par PU coupe la
droite D à 60°. Justification (Figure
du bas) Le triangle ACH est équilatéral. C'est une
propriété intéressante (surprenante !) liée à une sécante traversant deux
cercles selon certaines conditions. |
|
||
|
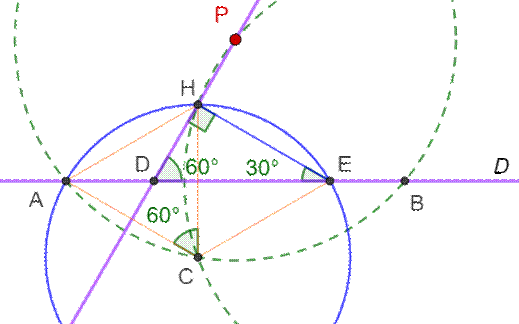
L'angle ACH vaut donc 60°. C'est un angle au centre qui intercepte l'arc AH. L'angle inscrit AEH intercepte le même arc: il
vaut la moitié: 30°. Dans le triangle rectangle DEH, l'angle HDE est
le complémentaire de DEH et vaut ainsi 60°. |
|
||
|
Cette
construction particulièrement astucieuse figure dans Euclidea
4.2. |
Son
fondement est expliqué sur la page des trois
cercles. |
||
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
DicoNombre |
|
|
|
|
|
Cette page |