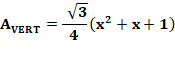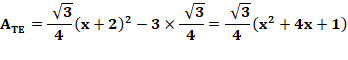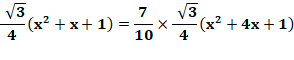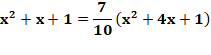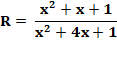|
Édition du: 24/11/2023 |
|
INDEX |
Hexagones |
||
Faites un double-clic pour un retour en haut de page
![]()
|
convexe équiangle Hexagone équiangle: hexagone dont tous
les angles sont égaux à 120°. |
||
|
|
Sommaire de cette page >>> Énigme de l'hexagone équiangle >>> Propriétés >>> Exemple de résolution |
Débutants Glossaire |
|
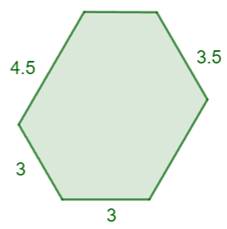
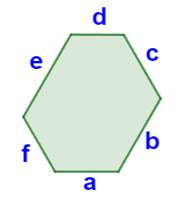
Énigme On donne cet hexagone dont tous les angles sont
égaux. Avec les seules dimensions
indiquées, est-il possible de calculer l'aire de l'hexagone ? Angles La somme des angles de l'hexagone convexe est
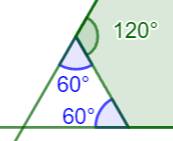
égale à celle de quatre triangles: 4 × 180° = 720°. La valeur de chacun: 720° / 6 = 120° Piste En prolongeant les côté de l'hexagone on forme un
triangle
équilatéral (illustration). En effet l'angle supplémentaire de 120° vaut 60°.
Et, un triangle avec deux angles de 60° est équilatéral. |
|
||
|
Les triangles équilatéraux Avec tous les prolongements des côtés, trois
triangles équilatéraux sont formés (bleus). Les angles en A, B et C sont égaux à 60°. Le
grand triangle ABC est lui-même équilatéral |
|
||
|
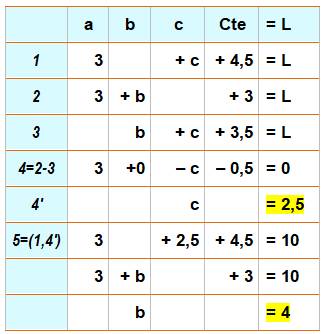
Calculs des côtés On pose les trois égalités donnant la valeur de
L. On note que: a = 3.
Notez la
disposition dans le tableau facilitant la résolution du système
d'équations. Par exemple, la 4e
ligne est la soustraction des lignes 2 et 3. |
Calculs de l'aire de l'hexagone
Voir Aire
du triangle équilatéral |
||
|
Un hexagone convexe
équiangle est inscrit dans un triangle équilatéral. Ses angles
internes valent 120°. Les côtés opposés
sont parallèles.
Quatre longueurs
suffisent à caractériser l'hexagone équiangle. Relations: |
|
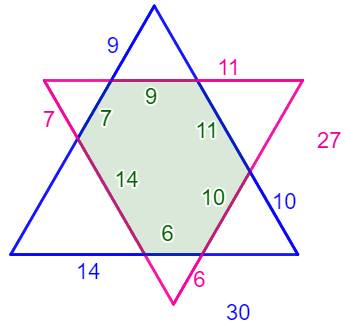
Deux façons de
dessiner le triangle équilatéral LBLEU
= 14 + 6 + 10 = 30 = f + a + b = b + c + d = d + e + f LROSE
= 6 + 10 + 11 = 27 = a + b + c = c + d + e = e + f + a
|
|
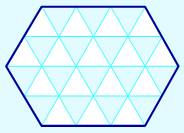
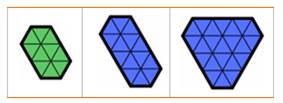
L'hexagone
convexe équiangle peut être pavé par des triangles équilatéraux.
Voir Autres exemples |
|
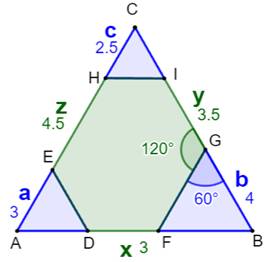
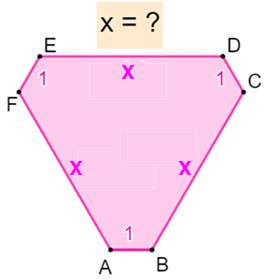
Énigme Un hexagone équiangle avec pour côtés: Quelles sont les valeurs possibles de x ? On donne: aire du triangle vert = 70% de l'aire
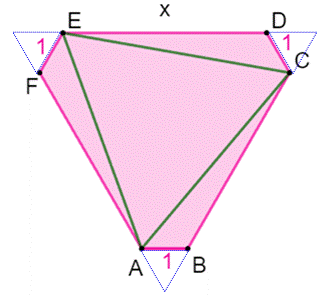
de l'hexagone. Piste (Figure
du bas) Deux temps:
Aire du triangle vert Dans le triangle ACE, les angles en A, C et E
sont égaux et le triangle ACE est donc équilatéral. Dans ABC, la loi
des cosinus donne: Aire du triangle ACE: Aire du triangle équilatéral En prolongeant les côtés, le grand triangle
équilatéral a un côté égal à x + 2, et les trois petits un côté égal à 1. Aire de l'hexagone: Relation (70%) Aire triangle vert = 70% aire hexagone:
|
Note sur le
70% La proportion exacte est: L'énoncé donne R = 0,7. Avec
un autre ratio la valeur de x serait évidemment différente. |
|
Haut de page (ou
double-clic)
![]()
|
Suite |
|
|
Retour |
|
|
Voir |
|
|
Sites |
|
|
Cette page |
http://villemin.gerard.free.fr/GeomLAV/Polygone/HexaEqui.htm
|