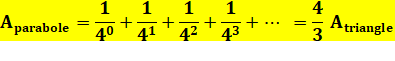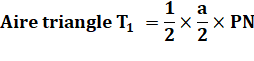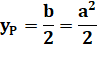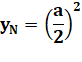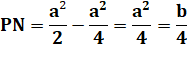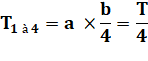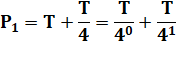|
|||||||||||||||||||||||||||||||||||||||
![]()
|
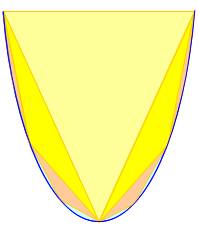
Aire du segment de parabole Quadrature de la parabole Méthode d'Archimède Archimède (-287 à -212 Syracuse en Sicile)
met au point une méthode d'exhaustion rigoureuse qui lui permet d'affirmer
que l'aire du segment
de parabole est égale à 4/3
de l'aire du triangle qui le sous-tend. La méthode d'exhaustion, connue avant
Archimède, consiste à approcher de plus en plus près l'aire à calculer par
excès et par défaut. Si les deux valeurs convergent vers la même limite, nous avons alors la
valeur de l'aire recherchée. Cette approche était connue sous le nom de quadrature, ancêtre du calcul intégral. Avec les techniques
actuelles, le calcul reste assez long. On ne peut qu'admirer le savoir-faire
d'Archimède. |
Anglais: Archimedes and his quadrature of a parabola / Archimedes'
quadrature of the parabola
Parabolic
section
Historique
|
Archimède, comme ses contemporains, avait
la réputation de faire connaitre leurs résultats,
mais jamais leurs méthodes. Les gardant
secrètes pour mieux dominer. C'est
faux! La preuve en a été donnée lors de la découverte en 1906 du palimpseste relatant en détail la
méthode de calcul du segment de parabole par Archimède. |
En
bref: Trisection du carré par deux paraboles (Archimède)
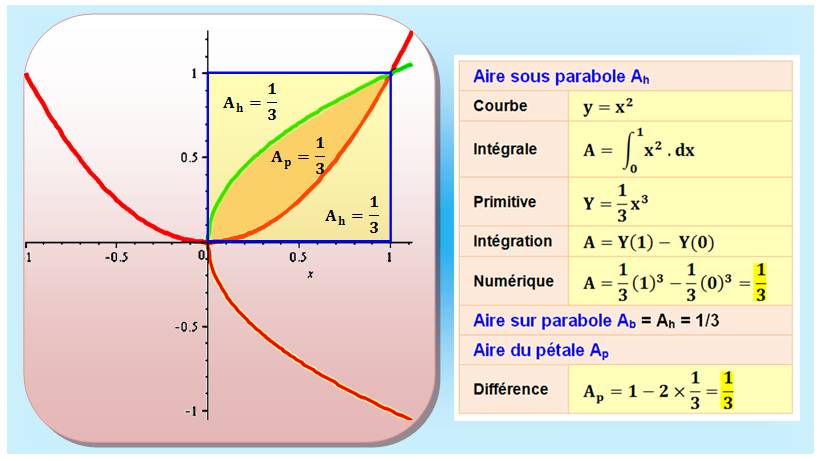
Voir Trisection
du carré / Calcul
par intégrale / Aires
/ Nombre
1/3
|
|
||
|
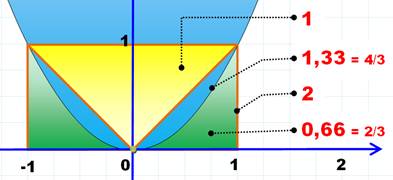
La
parabole (bleue) a pour équation y = x². Les points d'abscisse 1 et -1 ont
pour ordonnée y = 1 L'aire du
rectangle (en partie vert) est égale à 2 x 1 = 2. Celle du
triangle jaune est égale à la moitié: 1. On
considère le segment de parabole inscrit dans le rectangle (en partie bleu):
son aire est égale à 4/3 de l'aire du triangle. La composante bleue a une
aire égale = 4/3 – 1 = 1/3 |
|
|
|
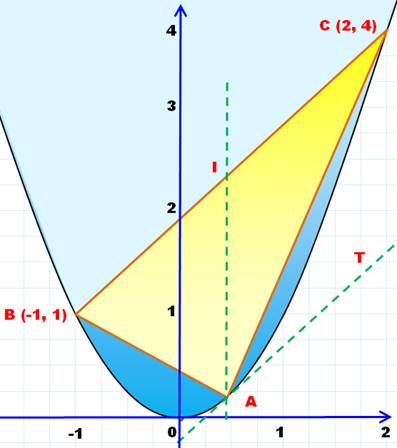
Prenons
deux points quelconques de la parabole (B et C). Construisons
le point A le plus éloigné de AB: La
parallèle AT à BC est tangente en A à la parabole. L'aire du
segment de parabole (bleu foncé) sous-tendu par le triangle ABC (jaune) est
égale à 4/3 de celle du triangle Archimède a démontré cette relation de
façon rigoureuse en approchant la parabole par excès et par défaut. L'aire du
segment est alors cernée. Note: il se
trouve que le point I à la verticale de A est le point milieu du segment AB. |
|
|
Voir Résumé des propriétés de la
parabole associées à celle-ci
|
|
||
|
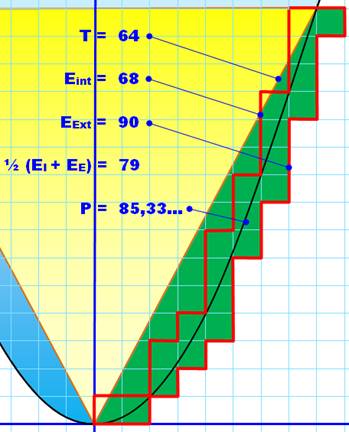
Une méthode la plus
classique consiste à créer une paire d'escaliers d'un côté et de l'autre de
la parabole. Le décompte des
mailles permet d'encadrer l'aire sous la courbe. Plus les mailles
sont fines et plus on approche par défaut et par excès la valeur exacte. Le principe est là.
Il se trouve qu'Archimède va utiliser cette méthode mais en la rendant plus
performante, plus mathématique. Il arrive à mettre
en formules itératives le calcul de ces deux valeurs. |
|
|
|
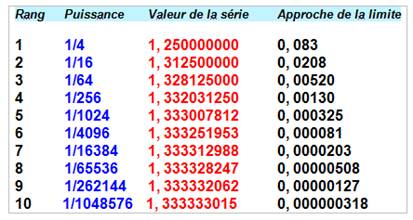
Archimède a calculé
ce rapport en dessinant de petits triangles dans la zone libre en bleue. Son
résultat Le rapport entre l'aire du segment
de parabole et celle du triangle est égal à 4/3. Et
cela est vrai dans le cas général. Prenons l'unité
comme aire du triangle jaune. L'aire des deux triangles jaunes foncés est
égale 1/4. L'aire des quatre plus petits en brun est égale à 1/8 = (1/4)² … |
|
|
|
La
démonstration complète fait appel à l'encadrement de la valeur par le haut et
par le bas, dite méthode par exhaustion. Archimède
avait approché la solution en faisant des pesées
imaginaires: la parabole et le triangle étant découpés en petites bandelettes.
La série géométrique,
calculée par Archimède
(287-212 av. J.-C.), semble être le premier exemple connu d'une série convergente. |
Convergence de l
|
|
Seules connaissances nécessaire pour le chapitre suivant
|
L'aire
du triangle est égale à ½ base L'équation
de la parabole la plus simple est y = ax² >>> |
|
|
||
|
|
||
|
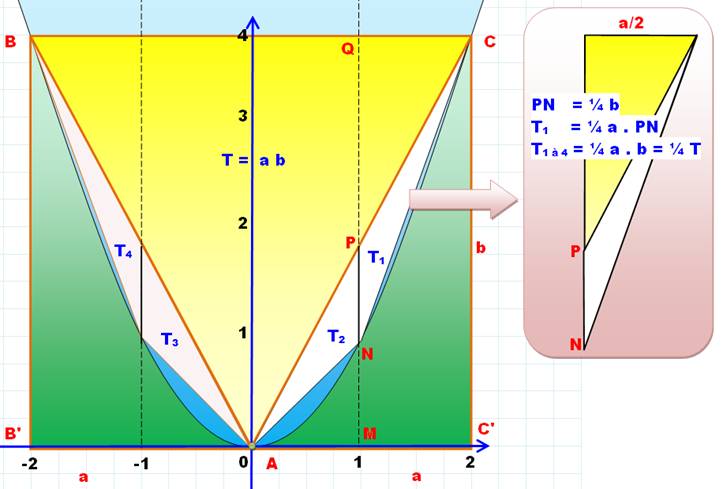
Parabole d'équation y = x² |
B (-a, b) et C (a, b) avec b = a² |
|
|
Rectangle (ici carré) BCC'B'
|
Aire rectangle = 2 a . b |
|
|
Triangle isocèle ABC dont l'aire est moitié de
celle du rectangle |
|
|
|
Triangle inséré ABN (blanc)
tel que |
M est le milieu de AC' |
|
|
Triangle T1 avec
base PN et hauteur QC |
|
|
|
Triangle T2 avec
base PN et hauteur AM |
|
|
|
Les quatre triangles
(surface blanche) |
|
|
|
Ordonnées du point P
d'abscisse a/2 (selon notre construction). |
|
|
|
Ordonnées du point N
d'abscisse a/2 (du fait de l'appartenance à la parabole: y = x²). |
|
|
|
Longueur du segment PN |
|
|
|
Aire de la surface blanche |
|
|
|
Cumul: aires de tous les
triangles à l'issue de cette première opération. |
|
|
![]()
|
Retour |
|
|
Voir |
|
|
DicoNombre |
|
|
Cette page |
![]()