|
||||||||||||||||||||||||||||||
![]()
|
Centre de Gravité
/ Barycentre Cette page est une page
d'introduction:
|
|
|
||
|
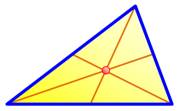
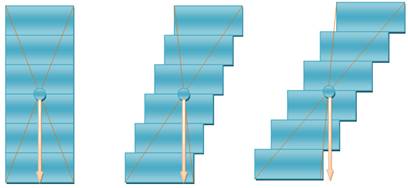
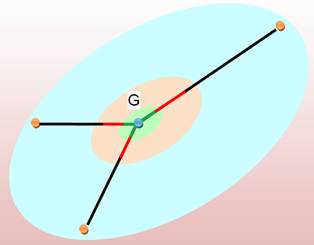
Du fait des symétries, ici, le centre de gravité est également le centre
géométrique, c'est-à-dire l'intersection des diagonales. Si la verticale passant par le centre de gravité passe à travers le
pied (la base) de l'objet, celui-ci
tient en équilibre; sinon (cas à droite), il tombe. |
Voir Calcul
du centre de gravité de cet escalier |
|
|
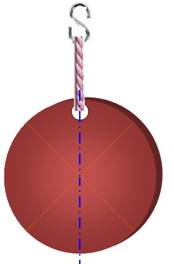
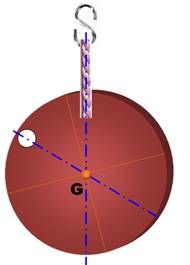
On suppose que
le disque est uniforme. S'il est plastique ou en métal, le matériau est
homogène et l'épaisseur est bien régulière. |
Repos Va se mettre en
mouvement |
|
|
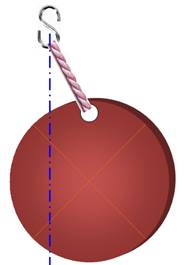
On néglige
l'effet du trou de fixation. |
Le point d'intersection de deux
lignes de gravité est le centre de gravité. C'est aussi une manière de
trouver le centre d'un disque. |
|
L'idée …
|
Pour
étudier le centre de gravité d'un objet ou d'un système formé de plusieurs objets,
l'idée consiste à d'abord s'intéresser au centre de gravité entre points
dotés de masses (en fait d'une pondération). Ce type de centre de gravité
s'appelle barycentre. Si
les "masses" sont toutes identiques, c'est l'isobarycentre. |
Voir Vocabulaire autour
du centre de gravité
|
|
||
|
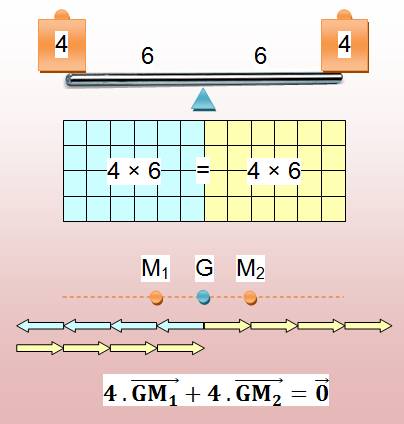
Barycentre de deux points de même
"masse"
Visualisation des influences
Position des deux points M1 et M2
|
Note: la flèche bleue de GM1 est dirigée vers la
gauche et celle de GM2 va vers la droite; les deux de même longueur, ajoutées,
s'annulent. Au lieu de flèche, en math et en physique, on dit vecteur. |
|
|
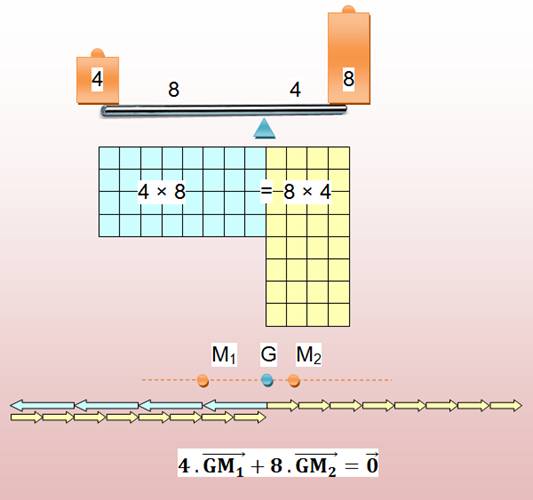
Barycentre de deux points de "masse"
différentes
Visualisation des influences
Position des deux points M1 et M2
|
|
|
|
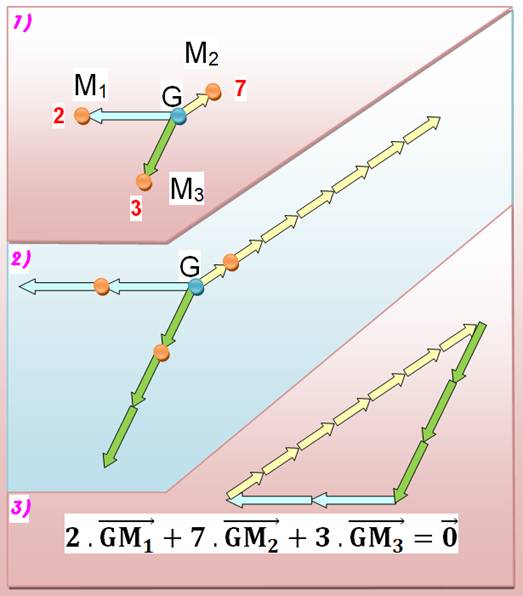
Barycentre de trois points de "masse"
différentes
Évidemment, ces figures successives ont été tracées en connaissant le
résultat final. Interprétation
|
|
|
|
|
||
|
Tout corps pesant a un centre
de gravité bien défini en lequel tout le poids du corps peut être considéré
comme concentré.
Le barycentre d'un
système matériel se meut comme si toute la masse du système y était
transportée, les forces extérieures du système agissant toutes sur ce
barycentre.
|
|
|
|
|
||
|
|
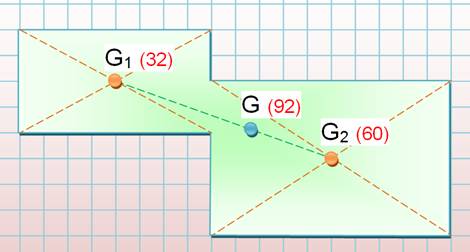
Le centre de gravité G
est le barycentre de G1 et de G2, chacun de ces points
étant le centre de gravité des rectangles élémentaires et chacun étant
pondéré de l'aire de ces rectangles. |
|
|
Nous
savons ce qu'est un centre de gravité, une sorte de centre de l'équilibre.
Lorsque l'objet est simple (disque, carré), le centre de gravité est le
centre géométrique de l'objet. Lorsque
l'objet est complexe, la position du centre de gravité se déduit du calcul du
barycentre des centres de gravité des objets élémentaires composant l'objet
complet. |
![]()
|
Suite |
|
|
Voir |
|
|
Aussi |
|
|
Cette page |
http://villemin.gerard.free.fr/aScience/Physique/CGDebut.htm
|