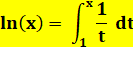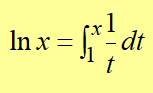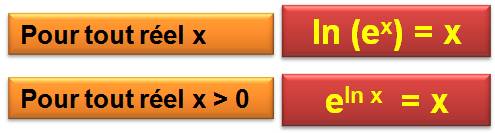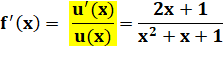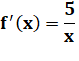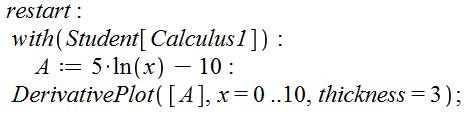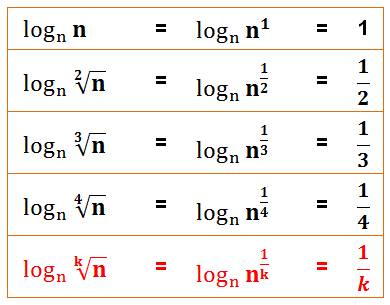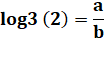Logarithme - approche, historique, définitions

NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 13/10/2023 Orientation générale DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Analyse
Débutants Logarithme	LOGARITHME				Glossaire Général
INDEX Analyse	Introduction	Calcul	Exemples	Changement de base
	Log et unités	Propriétés	Décibel	EXPONENTIELLE
	Log Discret	Table	Maths	Historique
	ln(1/x) = -ln(x)	x . ln(x) …	ln(x + 1) < x
		Sommaire de cette page >>> Approche >>> Types de logarithmes – Notation – Vocabulaire >>> Définition >>> Propriétés >>> Équations et inéquations >>> Étude d'une fonction logarithmique >>> Selon la base >>> Nombres en logarithmes >>> Logarithmes irrationnels

Humour

C'est Logarithme et Exponentiel qui sont dans un bar. Ils commandent une bière chacun. Lequel des deux paie?

Réponse: c'est Exponentiel parce que Logarithme népérien.

Voir Pensées & humour

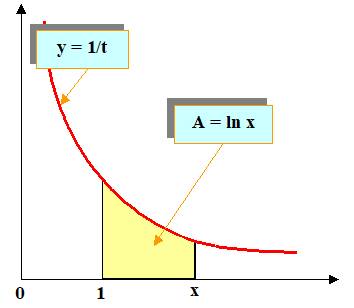
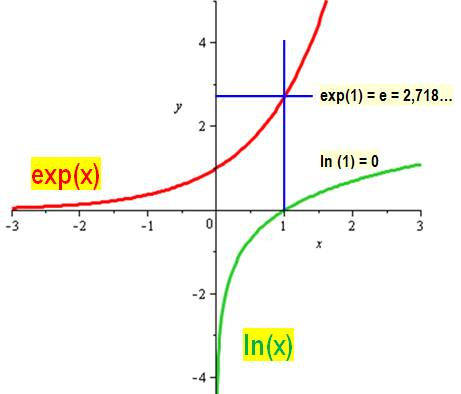
Maths à savoir en classe de terminale

La fonction logarithme népérien est l'unique fonction f(x), définie et dérivable sur l'intervalle: ] 0, + [ , et qui vérifie:

f(1) = 0 et f'(x) = 1/x.

Autrement dit: ln(x) est la primitive de sur ] 0, + [ qui s'annule pour x = 1.

Ou encore: pour tout réel x > 0:

Voyons cela pas à pas …

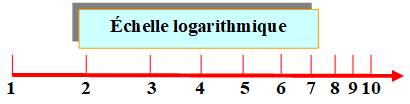
LOGARITHMES

Nombres qui "raccourcissent" les très grands nombres

et qui transforment les multiplications en additions.

Anglais : Logarithm

Calcul de la longueur d'un nombre avec les logarithmes

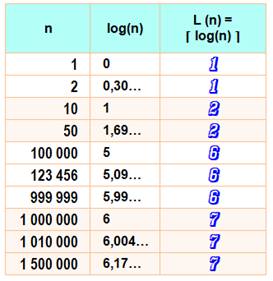
Le logarithme décimal d'un nombre indique la longueur du nombre.

La quantité de chiffres dans un nombre entier est égale à la valeur plafond du logarithme décimal.

Vrai, sauf pour les puissances de 10 (voir le tableau). Alors, on utilise cette formule avec la valeur plancher plus 1:

Voir Programmation avec les chiffres / Exemple de calcul

Voir Application à la recherche de palindromes

Voir Logarithmes pour débutants / Introduction avec les puissances de dix

APPROCHE

Logarithmes

Il a différentes manières d'envisager les logarithmes:

ARITHMÉTIQUE

ANALYSE

GÉOMÉTRIE

Correspondance entre progressions
géométrique (décroissante)

et arithmétique.

Logarithmes

et exponentielles

sont des fonctions réciproques.

Aire définie

par la surface

sous l'hyperbole.

Logarithme et surface (aire)

Le logarithme népérien de x est égal à la somme de 1/t pour toutes les valeurs réelles de t allant de 1 à x. (intégrale)

Voir

Pourquoi l'hyperbole

Avec x = e

Pourquoi e = 2,718

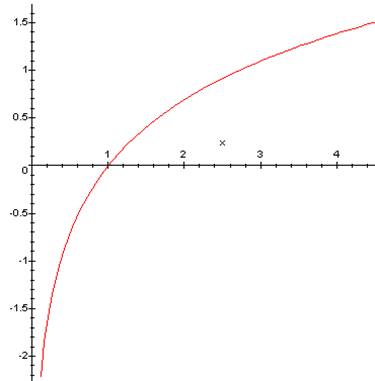
Courbe ln(x)

x	0	1
ln (x)		0

TYPES DE LOGARITHMES – Notations
Général	base a	log_a	logarithme base a logarithm to base a
Calculs numériques	base 10	log₁₀ log	logarithme base 10 ou décimal ou vulgaire ou de Briggs common logarithm or briggsian logarithm
Théorie mathématique	base e	log_e ln Log	logarithme naturel ou népérien natural logarithm or Napierian logarithm

En rouge, la notation la plus usuelle

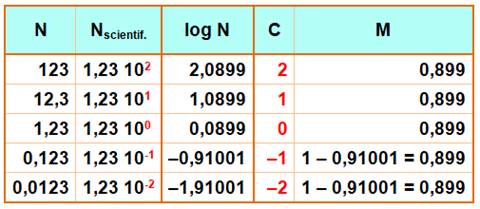
Caractéristique C

& Mantisse M

Notez leurs valeurs pour les nombres négatifs.

Le même nombre garde sa mantisse et change de caractéristique s'il est multiplié par une puissance de 10.

Voir Mantisse en notation scientifique

DÉFINITION

LOGARITHMES NATURELS

Fonctions bijectives réciproques

y est le logarithme
(progression arithmétique).

x est l'antilogarithme
(progression géométrique).

Logarithme Exponentielle

y = ln x si x = e^y

On peut écrire aussi:

Généralisation: logarithme de base a

y = log_a x si x = a^y

Soyons précis - Domaine de définition

En effet, reportons nous aux graphes de ces deux fonctions:

Propriétés – Formules
Fondamentale: multiplication à l'intérieur devient addition à l'extérieur
log_a	(x . y)	=	log_a x	+ log_a y
Attention
log_a	(x + y)	=	???
Autres
log_a	1/x	=	– log_a x
log_a	x / y	=	log_a x	– log_a y
log_a	x ^r	=	r	. log_a x
log_a	(x ^r. y^t)	=	r . log_a x	+ t . log_a y
log_a		=	1/2	. log_a x
Changement de base
ln	x	=	1	/ log_x e
	1	=	log_a b	/ log_b a
log_a	x	=	log_b x	/ log_b a

Suite en Changement de base / Application aux puissances à étages /

Équations avec inconnues en exposant

Valeurs
ln	e	=	1
log_a	a	=	1
Développements
ln (1 + x)	=	x – x²/2 + x³/3 – x⁴/4 + x⁵/5 – …
ln (1 – x)	=	– x – x²/2 – x³/3 – x⁴/4 – x⁵/5 - …
ln (2)	= =	1 – 1/2 + 1/3 – 1/ 4 + 1/5 – … 1/2 + 1/12 + 1/30 + 1/56 + … >>>
Limites
ln x	x	=
ln x	x 0⁺	= –
ln x / x^k		=	0	k entier
x^k . ln x	x 0⁺	=	0
ln x / (x – 1)	x 1	=	1
ln (1 + x) / x	x 0	=	1
Note (in petto): Pour se souvenir, on peut dire x croit plus vite que ln(x) ou x l'emporte sur ln(x).

Voir Zéro et infini

Équations et inéquations

Pour tous réels x ln(e^x) = x

Pour tous réels x >0 e^{ln
x} = x

Pour tous réels x > 0 et y >0, ln(x) = ln(y) x = y

ln(x) < ln(y) x < y

Pour tout réel x > 0 et pour tout réel a, ln(x) = a x = e^a

ln(x) < a x < e^a

Dérivée (sur un exemple)

f(x) = ln(x² + x + 1) = ln { u(x) }

La fonction interne au log doit être positive. De manière évidente elle l'est (même si x est négatif, x² l'emporte sur x). Plus sérieusement, le discriminant ( = b² – 4ac = 1 – 4 x1 x 1 = - 3) est négatif et a = 1 est positif, alors la fonction est positive.

La dérivée de x² + x + 1 est 2x + 1.

La dérivée de son log est:

Étude d'une fonction (sur un exemple)
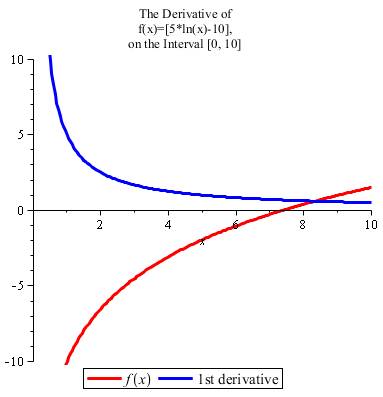
Fonction	f(x) = 5 ln(x) – 10
Valeurs typiques	f(1) = 5 ln (1) – 10 = –10 f(e) = 5 ln (e) – 10 = – 5
Domaine de définition	] 0 , + [
Limites
Dérivée	Positive dans le domaine de définition. La fonction est croissante
Variations Voir Graphe ci-dessous

Programmation du graphe – f(x) et f'(x)

Le package Student Calculus de Maple permet de tracer directement la courbe et sa dérivée.

Selon la BASE

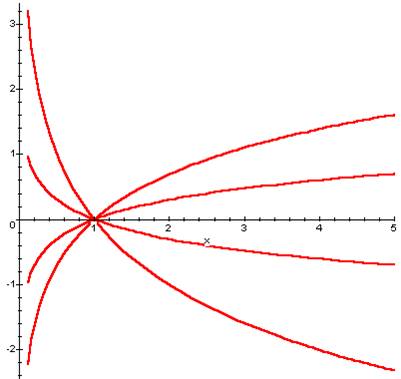
Passage par 1

Quelle que soit la base, toutes les courbes logarithmes passent par x = 1, y = 0 Car log_a 1 = 0
Lorsque la base est inférieure à 1, la courbe logarithme s'inverse

	e
	10
	0,1
	0,5

Passage par a

La courbe logarithme base 2 coupe la droite y = 1 en 2

La courbe logarithme base 3 coupe la droite y = 1 en 3, etc.

La courbe logarithme base a coupe la droite y = 1 en a

Car log_a a = 1

Nombre en logarithmes (amusement)

Tout nombre rationnel peut être atteint par les logarithmes

Logarithmes des inverses des puissances de 2

En combinant les deux résultats

Voir Jeux des quatre 4

Logarithmes irrationnels
Démonstration sur un exemple	log₃ (2) est irrationnel
Supposons qu'il soit rationnel. a et b nombres entier positifs (car un logarithme est toujours positif) avec b non nul.
Selon la définition du logarithme:
Chaque membre élevé à la puissance b
Donc l'entier est une puissance de 3, tous ses facteurs premiers valent 3.	n = 3 x 3 x 3 …
Mais, l'entier n est aussi une puissance de 2	n = 2 x 2 x 2 …
Cette contradiction implique que notre hypothèse est fausse	log₃ (2) n'est pas rationnel
Tous les logarithmes de nombres rationnels positifs supérieurs à 1 sont des nombres irrationnels.

Suite	Logarithmes – Calcul Logarithmes et tout nombre Logarithmes discrets Les 17 équations qui ont changé le monde
Voir	Arrondis avec logarithmes Calcul des factorielles avec les logs Croissance Constantes Mathématiques Courbes élémentaires Échelle de Richter Exponentielle Exposants – Index Exposants et puissances Limite de ln(x) / x et de x . ln(x) Morphisme
DicoNombre	Ln 2 = 0,693… Ln 10 = 2,302 …
Livre	Méthod'S mathématiques Terminale S – Bruno Clément – ellipses – 2012
Cette page	http://villemin.gerard.free.fr/Wwwgvmm/Analyse/Logarith.htm

Historique >>> (report de lien)