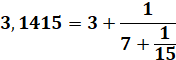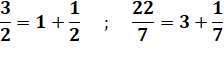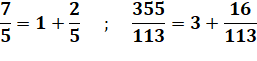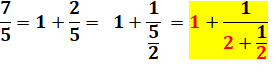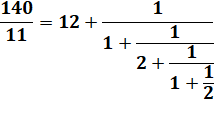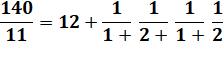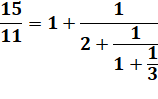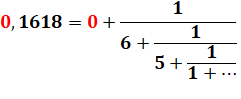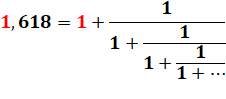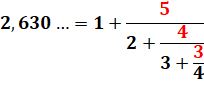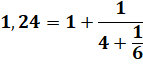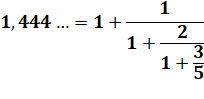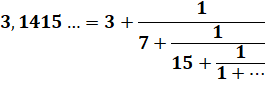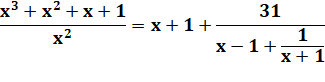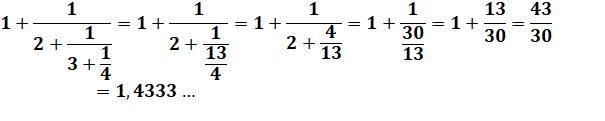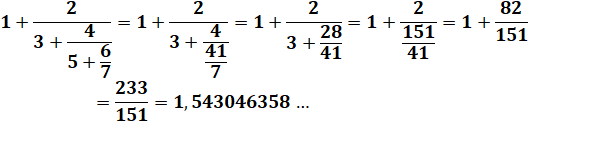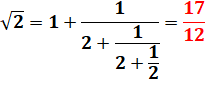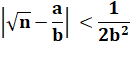|
||||||||||||||||||||||||||||||
![]()
|
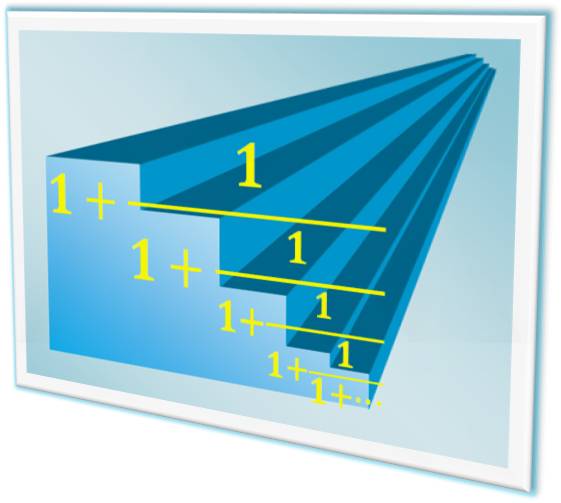
FRACTIONS CONTINUES ou
"fractions à étages" Fractions
de type escalier qui descend (souvent) sans fin.
Cette fraction continue est égale au nombre d'or Les fractions continues sont très utiles pour
calculer les meilleures
approximations de nombres réels. |
Anglais: Continued fraction
|
|
||
|
Pour apprécier une quantité,
on donne souvent une fraction qui approche la valeur, ou des sommes de
fractions. |
Cet
objet mesure 5,51 cm Ou
environ: 5
cm et demi, soit 5 + 1/2 Ou
précisément: 5
+ 1/2 + 1/100 |
|
|
Parfois, pour être plus
précis: on utilise des fractions à étage. |
Par exemple: constante
Pi
|
|
|
Fraction simple Fractions avec numérateur unité Fractions avec numérateur quelconque |
|
|
|
Fraction à étages Fractions avec plusieurs barres de fraction. |
|
|
|
Notations abrégées (numérateurs à 1) Fraction continue développée Notation abrégée classique Alternative (dite à la française) |
140 / 11 = [12 ; 1 , 2, 1 , 2]
|
|
Construction avec l'algorithme
d'Euclide
|
Convertir 15 / 11 en fraction continue:
15 / 11 = [1, 2,
1, 3] |
|
Voir Calcul de la fraction continue de e
|
|
||
|
Premier terme à 0 ou 1 ou
quelconque. |
|
|
|
Numérateurs à 1 ou quelconque Note: les numérateurs peuvent
être tous différents. |
|
|
|
Fraction continue finie ou
infinie Note: le nombre réel peut être décimal, périodique
ou non périodique. La valeur
d'une fraction continue arrêtée au rang n
est une approximation du nombre N
qu'elle représente. Cette fraction est appelée réduite.
C'est la meilleure approximation et en passant aux rangs suivants, les
réduites convergent vers le nombre N. Voir DicoMot / Racine de 2 |
|
|
|
Fraction continue algébrique |
|
|
|
|
|
|
À partir de ces exemples de calcul, vous pouvez
imaginez comment passer d'une fraction simple à une fraction continue: en
faisant le chemin inverse de celui montré ci-dessus. |
|
|
|
||
|
La fraction continue tronquée est appelée réduite du nombre. (Anglais: convergent; terme qui
apparaît aussi en français). La succession des réduites encadre le nombre par défaut
pour les dénominateurs pairs et en excès pour les impairs. On dit que la réduite offre une approximation diophantienne du nombre
irrationnel. Et c'est la meilleure approximation possible du nombre
irrationnel avec des fractions. |
Exemple: 3e réduite de racine de 2
Théorème de la meilleure approximation Si la réduite s'écrit N/D, alors l'écart entre ce
nombre rationnel et le nombre irrationnel qu'elle représente est inférieur à
1/D². Exemple 17/12 = 1,41666…
1/12² = 6,94…10-3 |
|
|
Théorème de la meilleure approximation Condition pour qu'une fraction a/b soit une réduite
d'un nombre irrationnel n |
|
|
Voir Une démonstration en équation de Pell
/ Fraction continue et réduites de e
/ Réduites de
Pi
![]()
|
Suite |
|
|
Voir |
|
|
Site |
|
|
Cette page |
![]()