congruence des cubes

Édition du: 24/09/2020

INDEX Théorie des nombres Types de nombres	Arithmétique – Modulo
	Introduction	Théorie	Propriétés	Formulaire
	Applications	Calculs	Carrés	Cubes
	Jeux	Sun Zi	Mod 9, 10, 11	Carrés et Cubes
	Parité	7 ^ 7 ^ 7	Log Modulaire	11¹⁰ = 32 mod 71

CONGRUENCES avec les CUBES

Quelles sont les propriétés des cubes via leurs modulos?

Quelles sont les conditions pour qu'ils soient égaux à 1?

Sommaire de cette page

>>> Approche

>>> Observation

>>> Propriétés

>>> Valeur 1

Débutants

Opérations

Glossaire

Nombres

Voir Cubes et somme de cubes modulo 9

Approche – Quelques valeurs

Prenons le cas des premiers nombres au cube modulo 3.

Amusant: le modulo du cube est égal à celui du nombre. Est-ce toujours le cas?

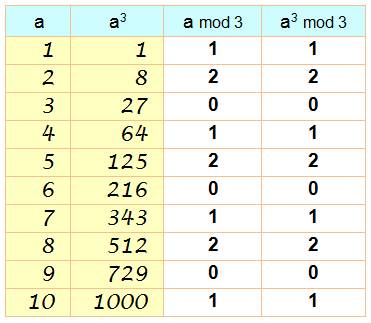
Pourquoi est-ce vrai avec m = 3 ?

Le reste de la division par 3 est soit 0,1 ou 2. Autrement dit:

Voyons les trois cas possibles:

0 x 0 x 0 = 0

1 x 1 x 1 = 1

2 x 2 x 2 2 mod 3

Effectivement

En modulo 2

0 x 0 = 0

1 x 1 = 1

Notes

Observez que pour a = 0, le reste est nul et 0³ = 0, soit 0 mod m quelle que soit la valeur de m.

Observez que pour a = 1, le reste vaut1 et 1³ = 1, soit 1 mod m quelle que soit la valeur de m.

Voir Introduction sur ce thème

Observations et propriétés

Tableau des nombres de 1 à 10, de leur cube, et des modulos de 2 à 10

Voir Tables - Index

Propriétés

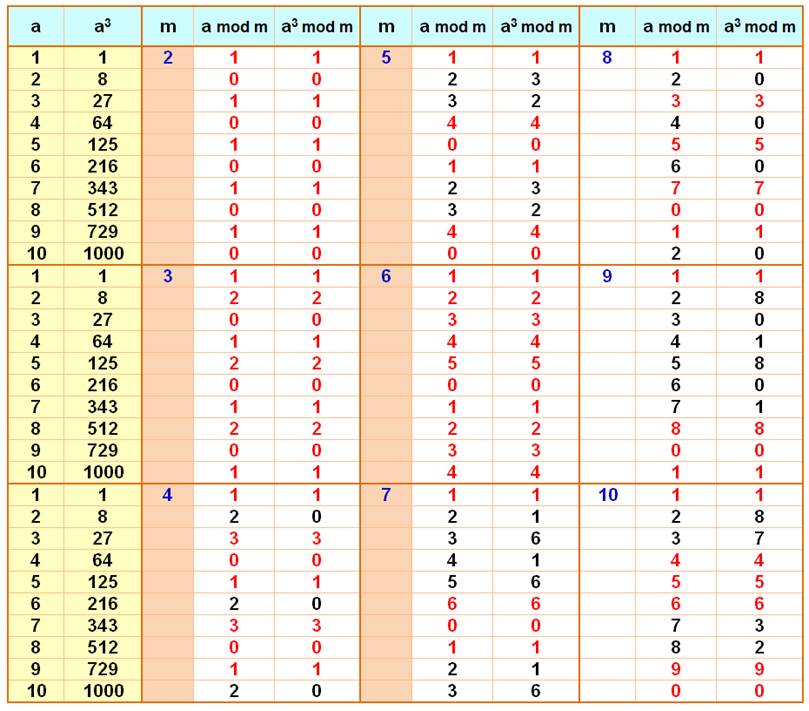
Première propriété: les valeurs prises

Voici le récapitulatif des valeurs prises par a³ mod m (en rouge) parmi toutes les valeurs possibles de a mod m.

Ces valeurs en rouge sont les résidus cubiques mod p. Les autres sont non-résidus cubiques. Anglais: cubic residue and cubic nonresidue.

Deuxième propriété: les égalités entre a mod m et a³ mod m

Toujours vraie pour a = 0 et les multiples de m quelle que soit la valeur de m. Également pour tout multiple plus 1. (Voir notes).

Toujours vraie, quelle que soit la valeur de a:

Souvent vraie selon la valeur de a:

sauf a = 4k + 2

sauf a = 5k + 2 ou a = 5k + 3

sauf a = 8k + 2 ou a = 8k + 4 ou a = 8k + 6

Cas de m = 9: vraie pour les valeurs limitées à 0, 1 et 8 sur neuf possibilités.

que si a = 9k – 1 ou a = 9k ou a = 9k + 1

Cas de m = 7: vraie pour les valeurs limitées à 0, 1 et 6 sur sept possibilités.

que si a = 7k – 1 ou a = 7k ou a = 7k + 1

Cas de a³ 1 mod m

Observons tous les cas où cette égalité apparaît (lignes marron clair)
On porte deux indications complémentaires: la valeur du plus grand commun diviseur (pgcd) de a et m; et, les cas pour lesquels a est un multiple de m plus 1.

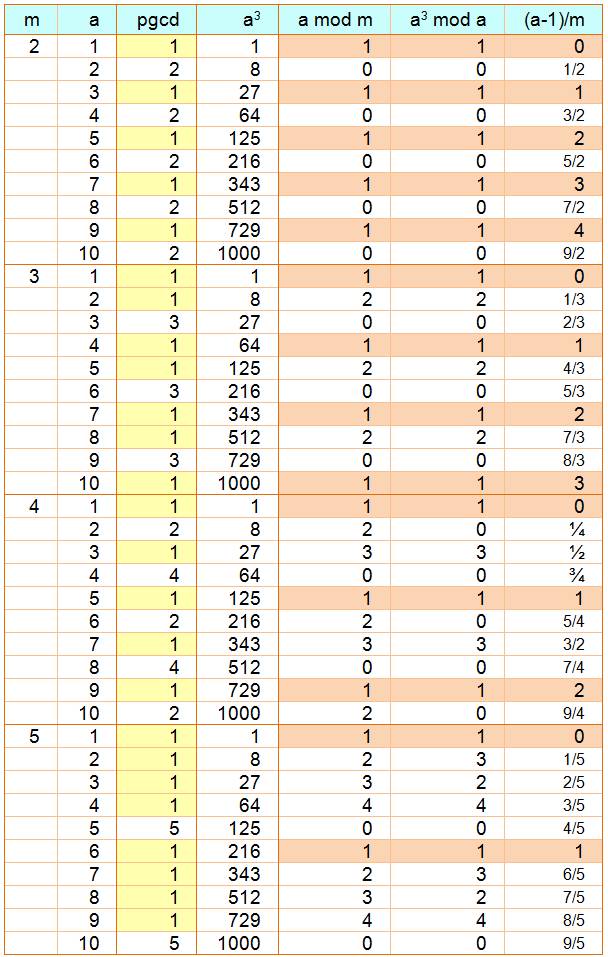
Conclusions

a³ a mod m pour a = k.m + 1, quelle que soit la valeur de m. Et ce sont les seuls cas.
Dans ce cas pgcd (a, m) = 1.

Explications

Congruence d'un cube:
si a b mod m alors a³ b³ mod m

Congruence égale à 1 selon notre hypothèse:

si b³ = 1 alors b = 1

Valeur de c en remplaçant dans la première expression:
a 1 mod m ou exprimé autrement a = k.m + 1

Dans la mesure où a est égal à un multiple de m plus 1, ces deux nombres sont premiers entre eux et leur pgcd vaut 1.

Attention:

Il est vrai que a³ 1 mod m alors a 1 mod m et a et m sont PEE.

Par contre, ce n'est pas parce que a et c sont PPE que a³ 1 mod m.

Exemple: 8 et 5 sont bien PEE mais: 8³ = 512 2 mod 5. (Dans le tableau, ce sont tous les cas de 1 en jaune, sans ligne marron clair en face)

Suite

Carrés et Cubes

Cubes et somme de cubes modulo 9

Congruences – Introduction

Voir

Unités des puissances

Division

Cette page

http://villemin.gerard.free.fr/ThNbDemo/ModCube.htm