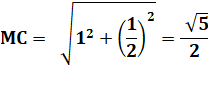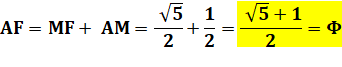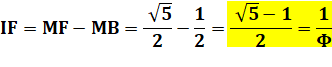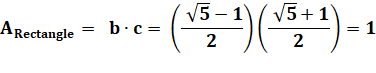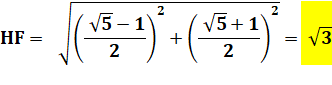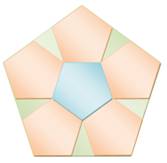
NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 31/01/2024 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Polygones
Débutants Géométrie	PENTAGONES				Glossaire Géométrie
INDEX Constructions Polygones Géométrie Terminale	Général	Données	Constructions
	Pentagone	Mesures	Méthodes générales	Cercles – Mascheroni
	Nombre d'or	Angles	Avec Racine de 5	Approchée de Dürer
	Pentacle	Segments	Avec bissectrices	Approchée originale
	Aire à partir de ses triangles		Méthode Euclide	Dissection
	Sommaire de cette page >>> Construction du triangle isocèle 32-72-72 >>> Construction du pentagone – Euclide >>> Construction dorée d'Euclide >>> Construction dorée du Pentagone >>> Rectangle et carré >>> Triangle doré – Justification			Voir Pentagones de Dürer

PENTAGONE RÉGULIER – Construction

Méthode d'Euclide

Plusieurs méthodes de construction du pentagone régulier dont celle basée sur la construction d'un triangle isocèle préalable, puis des bissectrices, à la façon d'Euclide.

Voir Angle Pi/5 = 36°

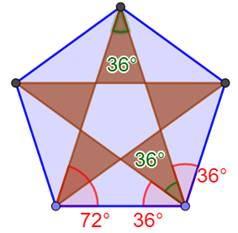
Construction du triangle isocèle 36-72-72 dit triangle d'or
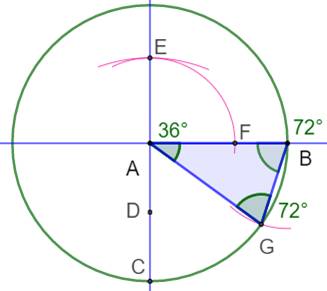
Un cercle et deux diamètres perpendiculaires sur AB et AC. Le point D est le milieu de AC. Cercle de centre C et de rayon CB. Intersection en E. Cercle de centre A et de rayon AE. Intersection en F. Cercle de centre B et de rayon AF. Intersection en G. Triangle 36-72-72: ABG Le triangle d'or est un triangle isocèle dont l'angle à la base vaut deux fois celui du sommet. Triangle que l'on trouve dans le tracé du pentagone avec son étoile à cinq branches. Voir Justification

Construction du pentagone – Euclide
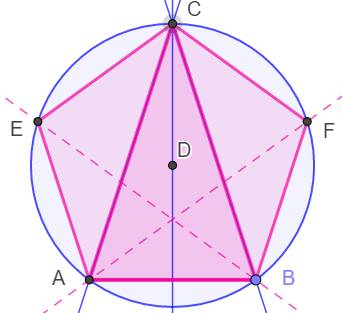
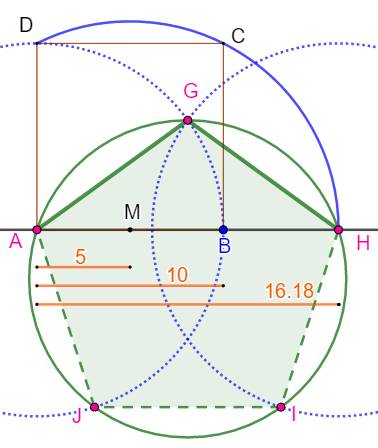
Euclide propose une méthode dessiner un pentagone dans un cercle. Il commence par montrer comment tracer un triangle doré dans le cercle à partir de celui dessiné ci-dessus. Nous passons cette étape. Nous disposons donc du triangle doré ABC construit selon la méthode indiquée ci-dessus. Construire le point D. C'est le point de concours des médiatrices des côtés. Cercle de centre D et de rayon DA. C'est le cercle circonscrit au triangle ABC. Bissectrices AF et BE des angles à la base du triangle isocèle ABC. Intersections en E et F Pentagone régulier: ABFCE	Le triangle ABC est un triangle d'or Côté: 1, Phi, Phi Angles: 36°, 72°, 72° ou Pi/5, 2Pi/5, 2Pi/5

Justification

Il s'agit de montrer que la construction proposée par Euclide conduit bien au tracé d'un triangle doré.

Deux étapes:

une construction dorée originale qui, par parenthèses, apparente cette méthode à celles impliquant la construction d'une racine de 5.

une justification dont le point de départ est cette construction dorée.

Construction dorée d'Euclide
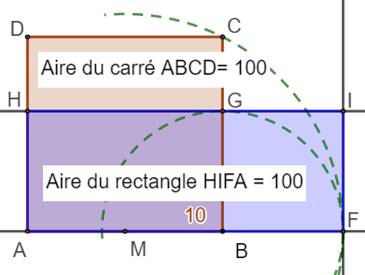
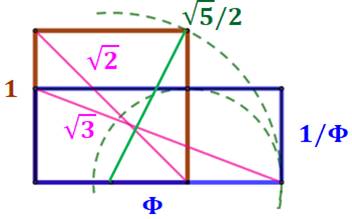
Dans son livre Les Éléments (II 11), Euclide propose une construction qui définit une égalité remarquable. Elle a trait au nombre d'or, même si ce nom n'était pas encore connu à l'époque. Construction Carré ABCD de côté 10 et aire = 100 Le point M est le milieu de AB. Le but est d'introduire une racine de 5 en MC Cette longueur MC est reportée sur la droite AB, créant le point F. La longueur BF est reportée en BG. La parallèle à AB et celle à BC en F définissent le rectangle HIFA. L'aire de ce rectangle et égale à celle du carré de départ.		Aire ABCD = Aire HIFA => AB² = AF.AH Et, en retirant à chacun ABGH: Aire DCGH = Aire BFIG => FI² = DC.DH
Justification Longueur du segment MC avec côté AB = a = 1.
Longueur de AF, l'un des côtés du rectangle Longueur de IF, l'autre côté du rectangle
Aire du carré (avec a = 1) Aire du rectangle
Longueur du segment HF, diagonale du rectangle
Longueur du segment AC, diagonale du carré
Résumé des propriétés de cette figure Aire grand carré = Aire grand rectangle Aire petit carré = Aire petit rectangle Avec carré de côté 1 Diagonale du carré = rac(2) Diagonale du rectangle = rac(3) Longueur du segment vert: rac(5) / 2 Longueur du rectangle = Phi Larguer du rectangle = 1/ Phi

Voir Brève 443

Rectangle et carré

Euclide raisonnait en termes d'aires pour comparer des égalités:

a² représente l'aire du carré: il dit, comme nous, le carré de a

b.c représente l'aire du rectangle: il dit, par analogie, le rectangle de b et c

Les livres anglais, américains ou indiens adoptent encore aujourd'hui cette formulation.

A rectangle whose adjacent sides are AB, AD is denoted by the rect. AB,AD; this is equivalent to the product AB.AD.

Notations utilisées dans le calcul de la puissance d'un point par rapport à un cercle.

Voir Théorème de Pythagore

Construction dorée du Pentagone
Construction dorée (du nombre d'or) On reprend la construction d'Euclide: AB = 10 (côté du pentagone, donnée de départ). Son milieu M. Carré ABCD. La longueur MC vaut Phi (cf. ci-dessus). Elle est reportée sur AB en AH (arc de cercle bleu). C'est la diagonale du pentagone. Construction du pentagone Triangle isocèle GAH avec GA = GH = 10 Construction à l'aide des cercles (bleus en petits pointillés). Les points A, G et H sont trois sommets du pentagone. Les deux autres sont obtenus en construisant le cercle passant par ces trois points. Son centre est le point de concours des médiatrices de GA et GH. Sur ce cercle, les points I et J sont les points de concours avec les deux bleus en pointillés.

Voir Exposé de cette construction par Rémy Trotabas / Toutes les méthodes de construction du pentagone

Triangle doré – Justification
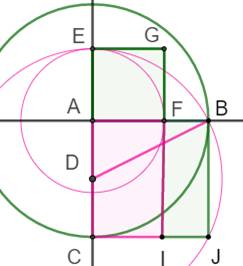
Ce qu'il faut démontrer La construction présentée crée bien un triangle isocèle dont l'angle à la base ets le double de celui du sommet. Démonstration On reprend le début de construction vue ci-dessus, jusqu'à la construction du point F. On y retrouve la construction dorée avec le petit carré AFGE et le petit rectangle FBJI dont les aires sont égales. Alors: AE² = FI.FB => AF² = BA.BF
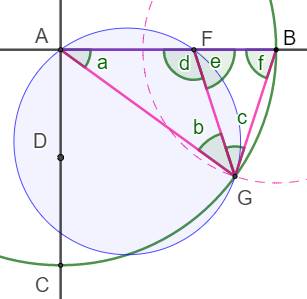
On retient les points AFB de la figure précédente. On trace le point G sur le cercle vert tel que BG = AF et le cercle qui passe par les trois points A, F et G. Notre relation: AF² = BA.BF = BG² Cette nouvelle relation montre que BG est tangent au cercle bleu. Interception de l'arc FG par l'angle FAG et par l'angle BGF (avec BG tangent) => angle a = angle c; on note a = c Les points B et G sont sur le cercle vert: le triangle ABG est isocèle et f = b + c = b + a Triangle AFG: e = 180 – d = 180 – (180 – a – b) = a + b Avec des angles égaux (f = e), le triangle GFB est isocèle. On a alors GF = GB = AF Avec deux côté égaux (AF et GF) le triangle FAG est isocèle. Alors: a = b = c L'angle en G (b+c) est bien le double de celui en A (a). Ce que nous voulions.

Retour	Construction avec bissectrices Pentagone – Généralités
Suite	Construction avec des cercles – Mascheroni Angles du pentagone Centre de gravité du pentagone Construction du pentagone Pentagone et le nombre d'or Pentagones de Dürer Hexagone
Voir	Calcul de Pi Constructions élémentaires Construction géométrique des nombres Dodécagone Géométrie – Index Pentagone et racines de 1 Polygone Pavage avec polygones Hexagone – Généralités
Site	Voir les liens en première page Construction of the Regular Pentagon – Berkeley
Cette page	http://villemin.gerard.free.fr/GeomLAV/Polygone/PentaEuc.htm