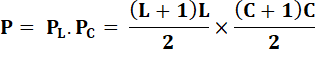![]()
|
|
Ce site est désormais accessible en |
|
22 Novembre 2025
![]()
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
Pour
ce rectangle, on sait que le demi-périmètre vaut 27 et l'aire plus la
différence entre longueur et largeur vaut 183. Quelles
sont les dimensions du rectangle ? |
|
|
|
|
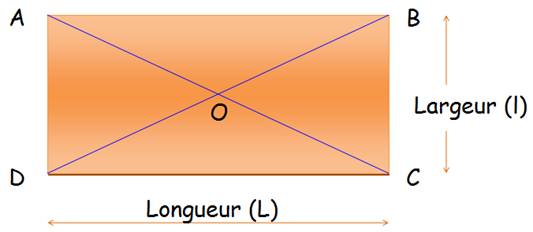
Rectangle
Il
suffit que trois d'entre eux soient droits. Mesures
Périmètre:
P = 2 (L + l) Aire: A = L . l Diagonale:
D² = L² + l² Aire AOB, ou BOC, ou COD, ou DOA = L.l / 4 Types
de rectangles
|
|
Voir Rectangle dans le DicoMot Maths
|
|
|
|
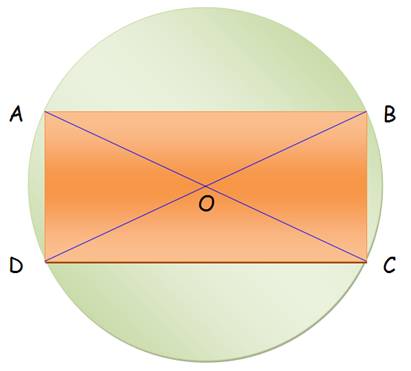
Les
quatre triangles découpés par les diagonales ont la même aire, égale au quart
de celle du rectangle >>>
|
|
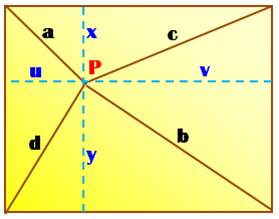
Point interne ou externe au rectangle
|
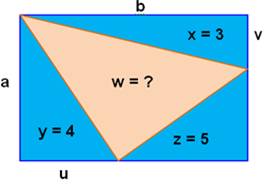
Le
Point P est quelconque. Propriété: a²
+ b² = c² + d² Démonstration
avec Pythagore a²
+ b² = u² + x² + v² + y² c²
+ d² = x² + v² + u² + y² Il
y a bien égalité. |
|
|
Autre interprétation : Aires bleues =
Aires roses
|
|
|
Un
point P dans un trapèze
isocèle de côtés parallèles AB et CD, alors:
|
|
Anglais
: British flag
theorem
Voir Brève 17-333
|
|
|
|
|
|
|
|
|
|
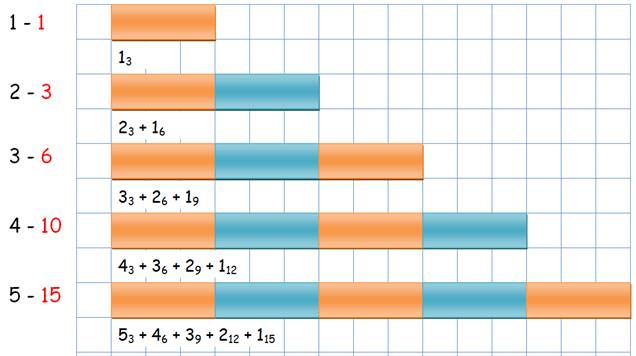
Exemple: pour n = 5 => 1/2 5 x
6 = 15 |
|
|
|
|
|
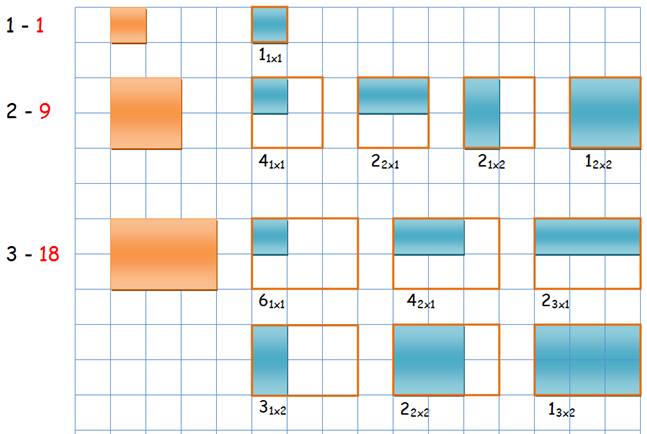
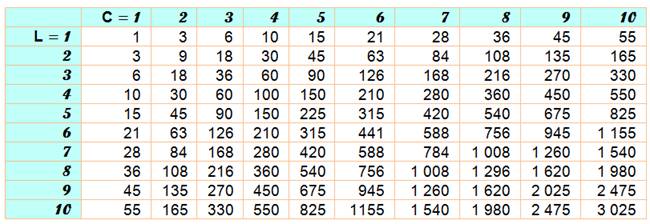
Quantité de
rectangles selon les valeurs de L et C
|
|
Voir Quantité de rectangles sur l'échiquier
(solution astucieuse par les diagonales)
Voir Brève 53-1055
|
|
||
|
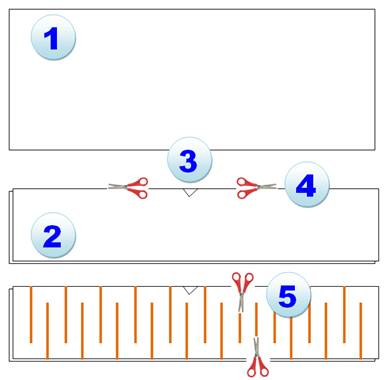
Puzzle classique du billet de banque. Vous pariez
que vous pouvez passer à travers le billet. Il suffit d'une paire de ciseaux.
Conseil: évitez le billet qui serait alors détruit. Prenez une feuille de
papier 1) Prenez un rectangle de papier plus long que large. 2) Pliez le en deux et 3) Faites un petit trou au milieu (passage pour y placer les ciseaux) 4) Coupez la pliure des deux côtés du petit trou jusqu'à environ 5 mm du
bord. Vous avez ainsi coupé la pliure sans aller jusqu'au bout. 5) Coupez comme indiqué: les coupes régulièrement espacées du haut à
presque le bas et, alternées, des coupes vers le haut sans aller jusqu'au
bout. 6) Vous obtiendrez une grande guirlande dans laquelle vous pourrez vous
glisser et gagner votre pari. |
|
|
Voir Énigmes
et puzzles / Magie
|
|
||
|
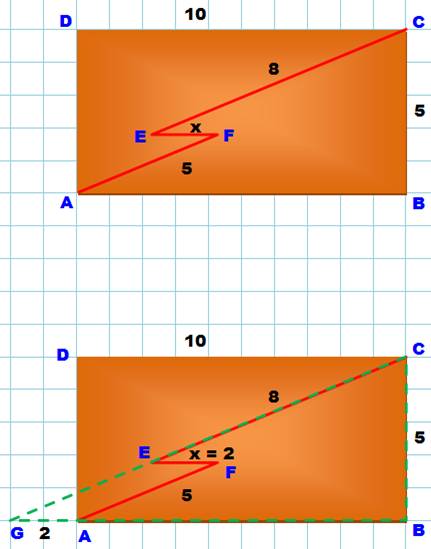
Énigme Un
rectangle 10 x 5. Une
diagonale brisée (8, x et 5) telle que EF est parallèle à AB.
De plus, AF est parallèle à EC. Avec ces
données, la construction est unique. Mais quelle est la valeur de x = EF? Solution Comme
souvent en géométrie, la solution
passe par un tracé complémentaire. Ici, le triangle
rectangle marqué par les pointillés verts. Alors, le
quadrilatère
AFEG, dont les côtés sont parallèles deux à deux, est un parallélogramme. Et: AF = GE => CG
= 8 + 5 = 13 Dans le
triangle rectangle GBC (vert), et avec le théorème de
Pythagore: GB² = GC² – BC² = 13² – 5² =
12² GB = 12 = GA + AB = GA + 10 x = EF = GA = 12 – 10 = 2 |
|
|
|
Vous pouvez
modifier les paramètres de cette énigme en conservant les relations
suivantes: |
AB = L, BC
= l et d = d1 + d2 L < d
Valeurs entières si l et d font partie d'un triplet de
Pythagore. |
|
|
Problème Pour
ce rectangle, on sait que le demi-périmètre vaut 27 et l'aire plus la différence
entre longueur et largeur vaut 183. Quelles
sont les dimensions du rectangle ? Solution Finalement
sont impliqués la somme, la différence et le produit des deux dimensions. On
écrit les relations puis on calcule:
Autres valeurs avec a = x + y et b = xy + (x – y) Les
plus petites: (a, b) = (4, 5) => (x, y) = (3, 1) Suivantes:
(a, b) = (5, 7) => (x, y) = (3, 2) et (4, 1) Avec
27, la plus petite: (a, b) = (27, 51) => (x, y) = (3, 24) et (26, 1) Avec
183, la suivante: (a, b) = (33, 183) => (x, y) = (38, 25) et (27, 6) |
Autres
énigmes: renvois de liens
Rectangle entouré
de carrés >>>
Aire du rectangle
dans le triangle rectangle >>>
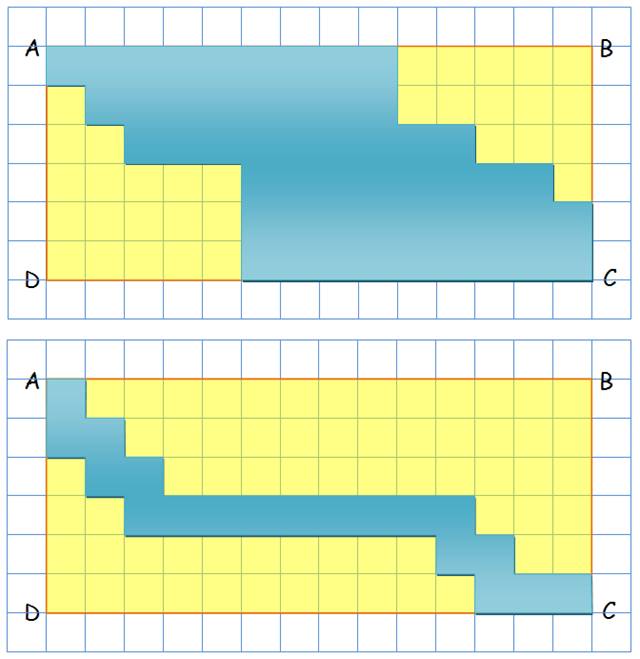
Rectangle coupé en
deux parties égales >>>
Rectangle partagé >>>
![]()
|
Suite |
|
|
Voir |
|
|
Cette page |
![]()