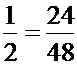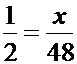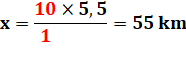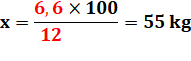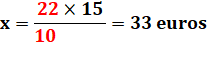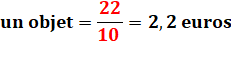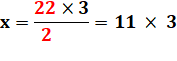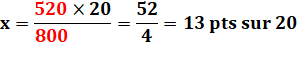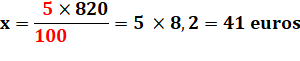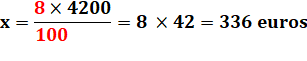Glossaire - pourcentage

RÈGLE DE TROIS

Proportionnalité

Quatrième proportionnelle

Approche

Nous disposons de deux fractions égales, une proportion;

Si pour une raison ou une autre, l'un des nombres vient à être effacé, il toujours possible de le retrouver:

Il s'agit de rétablir l'égalité des fractions:

Dans l'exemple, 1 est la moitié de 2;

Donc x est la moitié de 48, soit 24.

Définition

RÈGLE DE TROIS

Dans une proportion, recherche du quatrième nombre, connaissant les trois autres. Ce nombre est parfois appelé: quatrième proportionnelle.

Autre formulation: Recherche d'un coefficient a d'une application linéaire (exemple a = 1/2), puis calcul de l'image par cette application du troisième nombre donné (ici image de 48 => 48 x 1/2 = 24).

Le pourcentage est une règle de trois pour laquelle l'un des dénominateurs est fixé à 100.

Exemples de calculs
Si 1 cm représente 10 km sur la carte; 5,5 cm représentent x ?
Si 12 litres ont un poids de 6,6 kg; 100 litres pèsent x ?
En pratique: mettre les entités identiques l'une sous l'autre et faire le produit en croix
Si 10 objets coûtent 22 euros; 15 objets coûtent x ?
En théorie: si 10 objets coûtent 22 euros, alors un seul objet coûte 22 / 10 = 2,2 euros. Pour 15 objets, il suffit de multiplier par 15.
Dans ce dernier cas, le calcul mental peut opérer en remarquant que 15 / 10 c'est 3 / 2.
À son examen, il a obtenu un total de 520 points sur 800. Soit x points sur 20
Mon placement me rapporte 5 euros pour 100 euros (5%). x euros de rapport pour 820 euros placés.
Intuitivement: combien de fois 100 dans 820? Il y en a 8,2 fois. Soit autant de fois 5 euros.
Il fait un bénéfice de 8% sur le café. 8 euros de bénéfice sur 100 euros de vente x euros de bénéfice sur 4200 euros vendus.

Les proportions et les pourcentages

Il y aurait de l'ordre de 35 % des Français (en gros un sur trois) qui serait mal à l'aise avec les proportions, la règle de trois et les pourcentages.

En pratique

LE PRODUIT EN CROIX

Pour résoudre un problème de règle de trois:

- On écrit le produit en croix;

- L'inconnue apparaît dans une équation simple;

- Sa résolution en x donne la solution.

1	x
2	48

1 . 48 = 2 . x

x = 48 / 2 = 24

Exemple

Prenons des tomates à 2 euros les 4 kg.

Combien valent 7 kg ?

Le produit en croix donne 3,5 euros.

En effet le kg vaut 2 / 4 = 0,5 euros par kg.

Et 7 kg font: 7 x 0,5 = 3,5 euros

Euros	2	x
kg	4	7

x = 2 x 7 / 4

= 3,5

Types

La règle de trois peut-être

Simple

Inverse

Double

Combinée

…

Voir La règle de trois

Proportion

Deux fractions égales, une proportion.

Somme

La somme des numérateurs et celle des dénominateurs sont dans le même rapport.

En effet, écrivons le produit en croix.

On ajoute le même nombre de chaque côté.

Mise en facteur.

Mise en rapport (inverse du produit en croix).

Diiférence

La différence des numérateurs et celle des dénominateurs sont dans le même rapport.

Voir Démonstration du théorème de Thalès

Anglais	The rule of three (or rule of simple proportion). The method of finding the 4^th term of a proportion when the other three are given. Cross product. If four quantities be in proportion, the product of the extremes is equal to the product of the means.
Suite	La règle de trois - sa pratique, ses pièges!
En savoir plus	Règle de trois - Exemple de calcul Règle de trois et unités Preuve par neuf Pente Calcul d'un angle Énigmes avec calcul de double proportion
Et aussi	Aire du rectangle divisé en 16 Arc tangente Calcul mental - La méthode Fermi Calcul mental - Index Construction géométrique d'une fraction Fractions – Glossaire Taux d'intérêts Théorème de Thales Solution et soluté Exemple Voyager 1