|
|||||||||||||||||||||||||||||
![]()
|
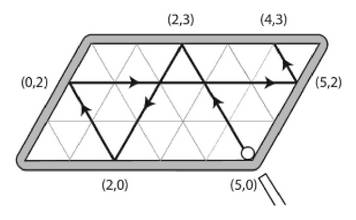
ÉNIGMES de TRANSVASEMENTS Diagramme triangulé Nous
avons utilisé un Ce diagramme utilise l'image d'un billard.
La bille lancée d'un point de départ rebondit sur les bords jusqu'à attendre
la valeur souhaitée. Illustration avec le problème de 8 litres d'eau dans
seau de 8 litres: comment mesurer 4 litres avec en plus un seau de 5 litres
et un seau de 3 litres (8; 8 , 5, 3 – 4)? Illustration
tirée du livre d'Alex Bellos |
|
|
||
|
Deux
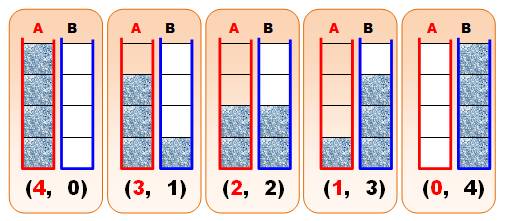
bidons A et B chacun pouvant contenir quatre litres d'eau. Nous
disposons de quatre litres d'eau. Le schéma montre les cinq façons de répartir
ce volume en quantités entières de litres dans chacun des deux bidons. |
À gauche, un bidon de 4 litres contenant
quatre litres d'eau et un bidon vide. Notation (4, 0) |
|
|
|
||
|
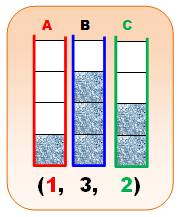
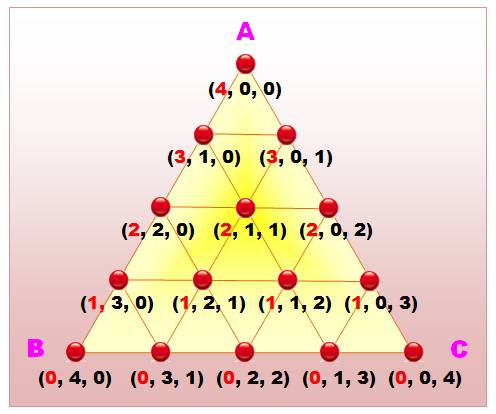
Toujours
avec quatre litres d'eau, quelles sont les configurations possibles? Nous
partons du contenu du bidon A et partageons le reste des quatre litres dans
les bidons B et C. En bas du
tableau, dans le cas où il n'y a pas d'eau dans A, nous retrouvons le cas de
deux bidons avec 4 litres, vu ci-dessus. |
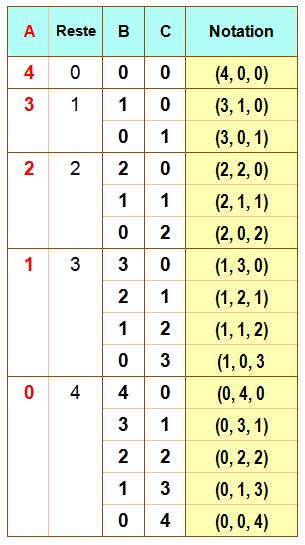
Les quinze configurations possibles avec 4
litres d'eau partagés entre trois bidons de 4 litres (en nombre entiers de
litres). |
|
|
|
||
|
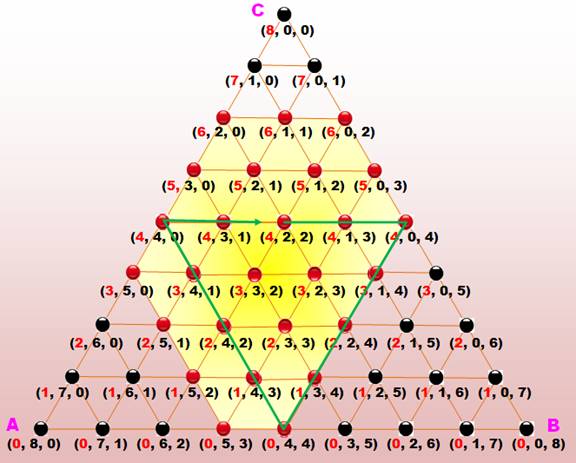
Une manière de représenter
les différentes configurations à trois bidons: le diagramme triangulé. En pointe la configuration: bidon A plein (4, 0,
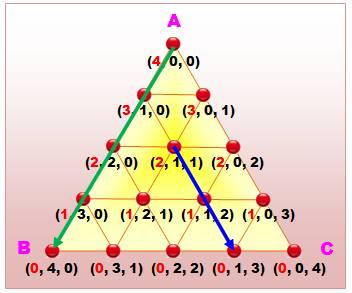
0). Chaque ligne
horizontale représente une configuration différente pour le bidon A (4
litres, puis 3 litres, …; en rouge). Observez les lignes obliques
descendantes: ce sont pour chacune un remplissage différent du bidon
B. Même chose pour les lignes obliques montantes et le bidon C. Un déplacement sur une ligne ne change pas le
contenu de l'un des bidons. Pratique! Le bidon A est plein et je le verse dans le bidon
B. Sur le diagramme, nous passons du sommet haut au sommet gauche (flèche
verte). Autre situation: bidon A avec 2 litres, B avec 1
litre et c avec 1 litre. Nous versons A dans C. Sur le diagramme, nous
passons de (2, 1, 1) à (0, 1, 3) trajet représenté par la flèche bleue. Un bidon vidé dans un autre conduit à une
configuration en bordure du grand triangle. |
Diagramme
Avec de diagramme, un bidon plein et les
autres vides est représenté par un sommet du triangle équilatéral. Bidon versé dans un autre
Les configurations en bordure du triangle
correspondent à l'un des bidons vide, au moins. |
|
|
|
||
|
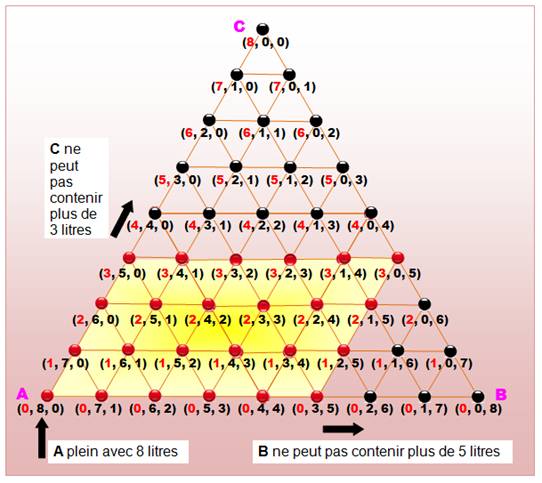
Nous
avons 8 litres d'eau à repartir dans trois récipients:
Reprenons
notre diagramme en forme de triangle équilatéral avec un côté égal à 8. Cependant,
deux des récipients ne peuvent pas contenir plus de 5 ou 3 litres. En versant les 8 litres de A dans C, ça déborde!
Le chemin qui va de A à C est impossible. On
élimine les points correspondants. D'où la découpe en parallélogramme. |
Le parallélogramme des possibilités est
obtenu en éliminant les configurations correspondant aux récipients trop
petits. |
|
|
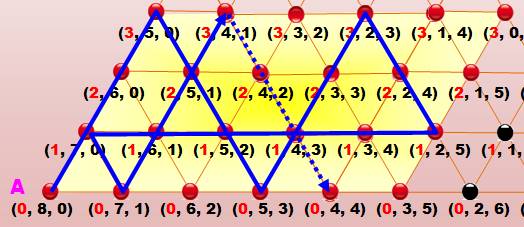
Notre objectif
est d'obtenir 4 litre d'eau dans un récipient en partant de 8 litres dans A. En remplissant C en premier, le trait bleu montre
comment atteindre le premier 4 litres. En effectuant un versement complémentaire, nous
avons deux fois 4 litres. |
En bleu, le chemin permettant d'atteindre
le premier 4 litres. En pointillé, le chemin pour deux fois 4
litres. |
|
|
Comme (4; 4, 2 ½
, 1 ½ – 2 ½ , 2 ½ ) |
||
|
|
||
|
Ici nous
disposons de 8 litres d'eau pour trois récipients plus petits: 6, 5 et 4
litres. Le
diagramme est épointé en ses trois sommets Selon le point de départ, tous les chemins ne sont pas faisables et
même certains sont cycliques (comme le vert représenté). |
|
|
|
|
||
|
Nous
venons d'utiliser un système de coordonnées trilinéaires sans le savoir. La somme
des trois coordonnées est constante (correspond au volume total de liquide). Reste
juste à normaliser la constante à 1. Avec l'exemple ci-dessus, la somme des coordonnées est toujours égale
à 8. |
En coordonnées trilinéaires:
|
|
|
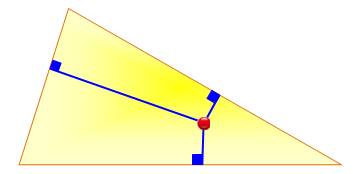
Si le
triangle est quelconque, les coordonnées sont dites barycentriques. Chaque coordonnées représente la distance du point à chaque côté
(éventuellement prolongé). La coordonnée est négative si le point est extérieur par rapport au
côté. |
|
|
|
Avec un
point P dans le triangle ABC équilatéral. |
Aire du triangle: ½ ax + ½ ay + ½ az = ½ ah x + y + z = h |
|
Anglais: Trilinear coordinates / Barycentric coordinates
Voir Définitions et
développements concernant es deux systèmes de coordonnées
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Sites |
|
|
Cette page |
![]()