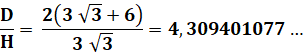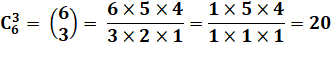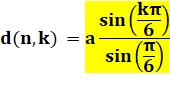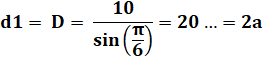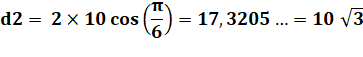|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
sous toutes les coutures Toutes
les mesures de l'hexagone de côté unité. |
Voir Leurs calculs / Construction
Flocons de
neige – Snowflakes

Photographiés
par Nathan Myhrvold – Artnet
|
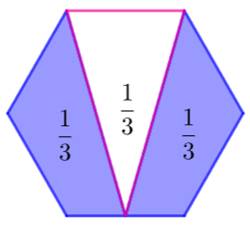
En rose, segment joignant un sommet
au milieu du côté opposé |
||
|
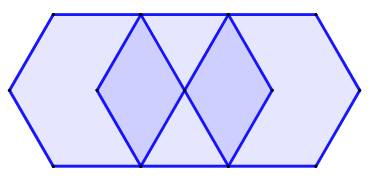
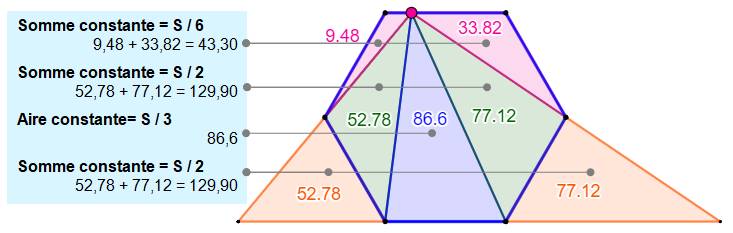
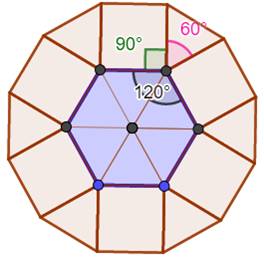
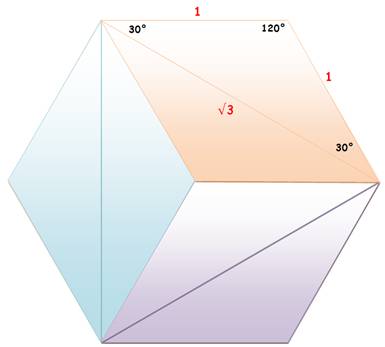
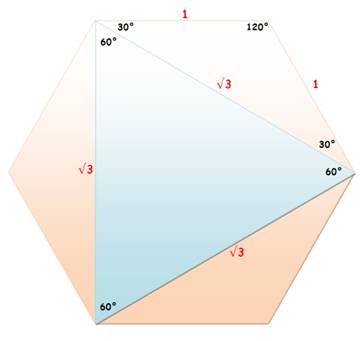
Explications Il
existe six triangles comme le triangle rose. Ensemble, ils couvrent deux fois
la surface de l'hexagone. Chacun
couvre 2H/6 = 1/3 Hexagone. Cette
aire étant connue, sur la figure en haut à gauche, chaque partie bleue,
symétriques, couvre également un tiers de l'hexagone. |
|
|
|
|
||
|
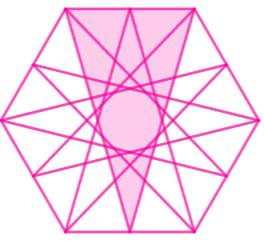
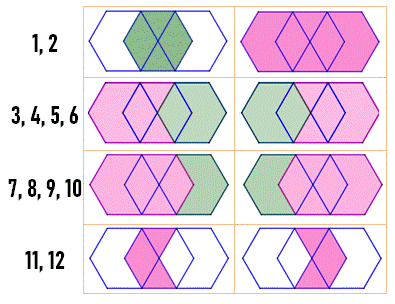
Énigme Sur cette
figure, trois hexagones réguliers enchevêtrés. Combien
d'hexagones comptez-vous: trois ou plus ? Oui, il faut compter tous les
hexagones réguliers, ou non. Solution La figure
contient douze hexagones. Ils sont
présentés ci-contre. |
|
|
Voir Brève
761
|
|
||
|
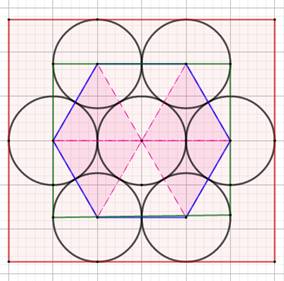
Un
hexagone est tel que ses six sommets sont entourés d'un disque de 1 m de
diamètre. Aire:
On calcule ces valeurs en remarquant que la
grande diagonale du losange vaut racine de 3. L'enveloppe
marron correspond au rectangle minimum permettant de loger sept personnes avec
un mètre de distance entre-elles. |
|
|
Anglais: hexagon hull
|
|
|||
|
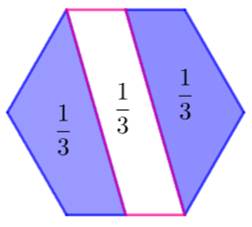
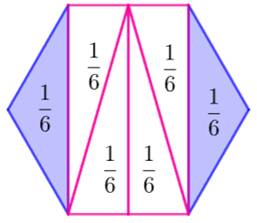
Hexagone Les
diagonales de l'hexagone le partagent en surface égale au sixième ou au tiers de l'aire totale.
Point
naviguant sur une côté Avec
les triangles ayant pour sommet un point situé sur une côté (point rouge),
les proportions des aires sont conservées:
soit avec la somme de deux d'entre eux ou alors intégralement pour le
triangle central.
Pourquoi
?
|
|||
Voir Énigme
de l'hexagone / Triangle dans
l'hexagone
|
|
||
|
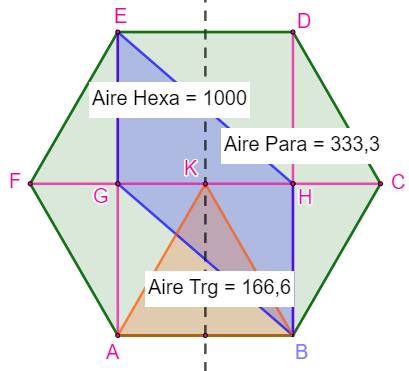
Propriété Ce parallélogramme bleu interne à
l'hexagone couvre une aire égale au tiers
de celle de l'hexagone. Démonstration Pour le voir,
on compare sa moitié GHB à l'un des six triangles équilatéraux qui couvent
l'hexagone: ABK. Avec même
hauteur et base égale, ces deux triangles sont égaux. Soit 1/ 6 de
l'hexagone. Aire du
parallélogramme = 1/3 de l'aire de l'hexagone. |
|
|
|
|
||
|
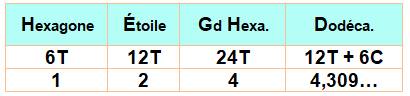
Hexagone
+ six carrés + six triangles équilatéraux => Dodécagone Sur
la figure, le marquage des angles montre que, l'angle au sommet de l'hexagone
étant égal à 120°, l'angle du triangle est égal à 60° (360 – 120 – 2 x 90). Ce
triangle ayant deux côtés égaux (côtés des carrés), il est équilatéral. Le périmètre du
dodécagone est le double de celui de l'hexagone. Aire de l'hexagone: H
= 6T (Triangles équilatéraux) Aire du dodécagone: D
= H + 6T + 6C = 2H + 6C
Rapport entre les
aires:
Aire du grand hexagone:
HH = H + 6T + 12T (losange
= 2T)
Rapports
entre toutes ces surfaces
|
Hexagone et dodécagone
Avec le grand hexagone
|
|
|
|
||
|
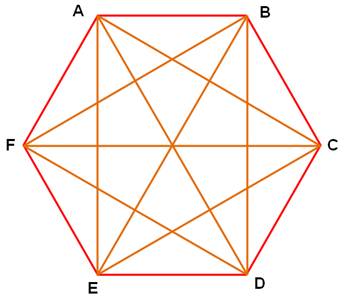
Quantité de diagonales
|
|
|
|
Quantité de triangles
|
||
Voir Compter les triangles dans une figure
/ Triangles monochromes dans
l'hexagone
Voir Triangles rectangles typiques
/ Diagonales dans les polygones
|
|
||||||||||||
|
Longueur
de la diagonale k, avec k la quantité de côtés interceptés par la diagonale. |
|
|||||||||||
|
|
|||||||||||
Voir Son calcul / Tables / Quantité
d'intersections des diagonales
|
|
||
|
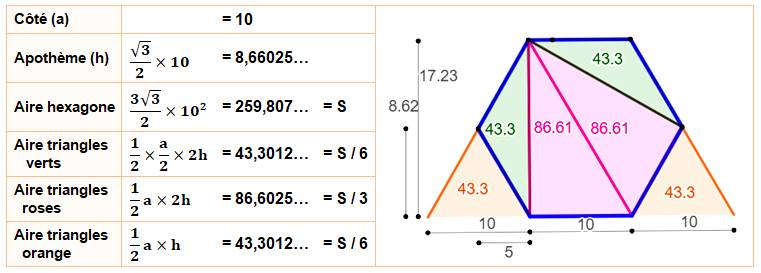
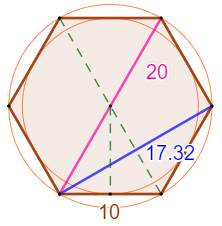
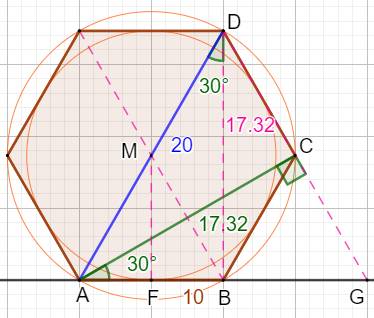
Exercice de géométrie Angle au sommet interceptant un côté
Diagonales
Rayon des cercles
Apothème
Calculs des longueurs
pour une longueur du côté: a = 10. |
|
|
|
Grande
diagonale, diamètre du cercle circonscrit: d1 = D = AD |
|
|
|
Petite
diagonale d2 = AC: |
|
|
|
|
||
|
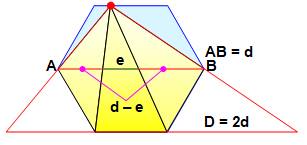
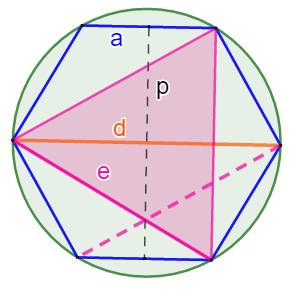
Un
hexagone de côté a. On sait que d = 2a. Valeur de
e, côté du triangle équilatéral ? Pour un quadrilatère inscrit, le produit des diagonales
est égal à la somme des produits des côtés opposés. a.a + a.d = e.e e² = a² + 2a² = 3a²
C'est la
même longueur que la médiane (pointillé) qui vaut deux fois l'apothème
(calcul via la hauteur d'un triangle équilatéral). |
|
|
|
|
||
|
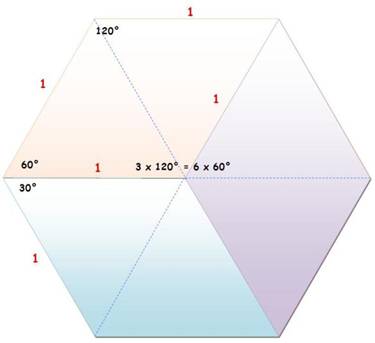
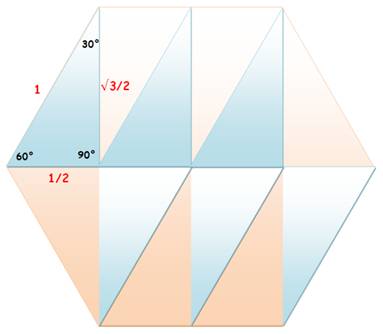
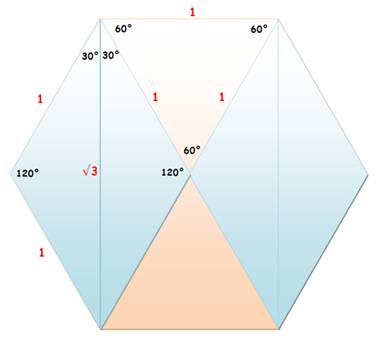
3 losanges 60 -120 de côté unité, ou 6 triangles équilatéraux unitaires. |
6 triangles isocèles 30-30-120 unitaires.
|
|
Voir Allumettes; comment transformer un hexagone
en cube?
Pavage
monohédral de l'hexagone avec parties non centrales

Voir Un
tel pavage pour le disque / le dodécagone
|
12 triangles rectangles 30-60 (6 en bleu et 6 en rose), ou 4 triangles rectangles 30-60 sur les côtés et 2
rectangles 1- |
2 trapèzes isocèles 60-120 de côté 1 et 2. |
|
2 triangles équilatéraux unité, plus 4 triangles isocèles 30-30-120, ou 2 losanges 60-120. |
1 triangle équilatéral en racine de 3, plus 3 triangles isocèles 30-30-120. |
Merci à Jean-Marc D.
|
|
||
|
Somme:
15 dont 6 côtés.
Résultat: 6 x 5 / 2 = 15. |
|
|
|
Ces
deux figures ont même périmètre.
Leur
aire est dans le rapport 2/3. |
|
|
||||||||||||||
|
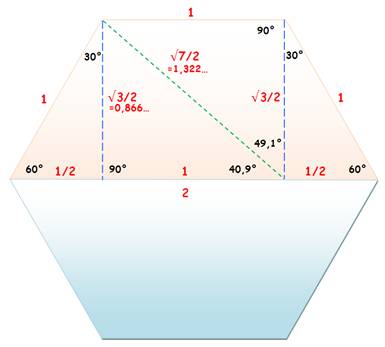
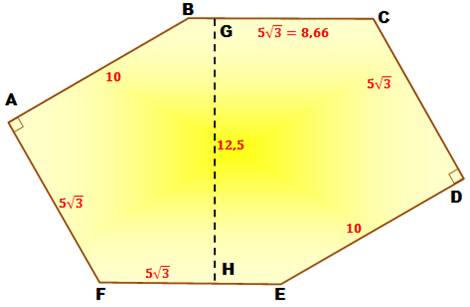
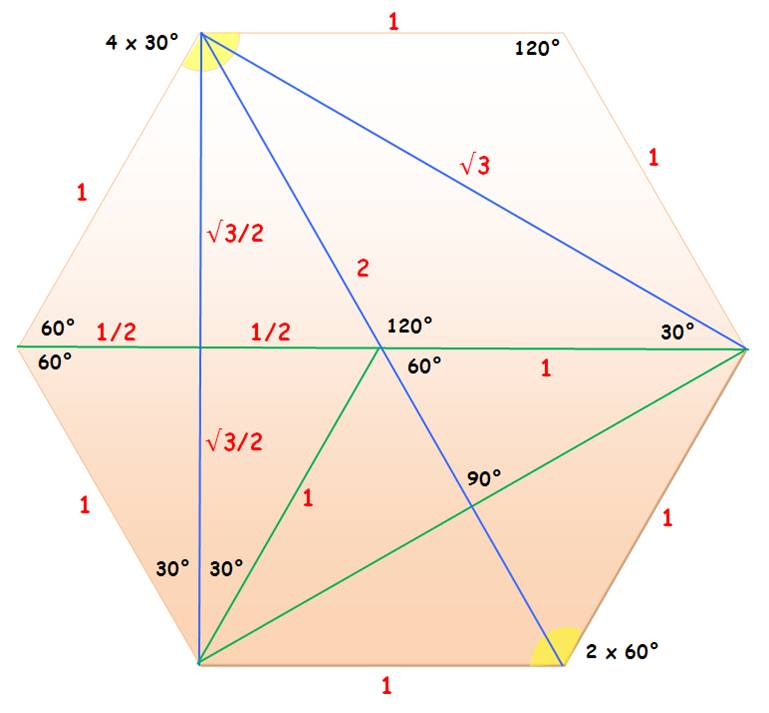
Une nomenclature
particulière de l’hexagone: il formé de six triangles rectangles (1) isométriques (égaux) qui
constituent la bande centrale. Et de quatre triangles rectangles (2)
semblables aux six autres, mais plus petits qui constituent les pointes. Ces deux types de rectangles sont rappelés à droite avec
leurs dimensions.Ce sont des demi-triangles
isocèles avec des angles de 30°
et 60°.
|
||||||||||||||
|
Le pentagone est le royaume de
la racine de 5, |
Rappel des lignes
trigonométriques
|
|||||||||||||
|
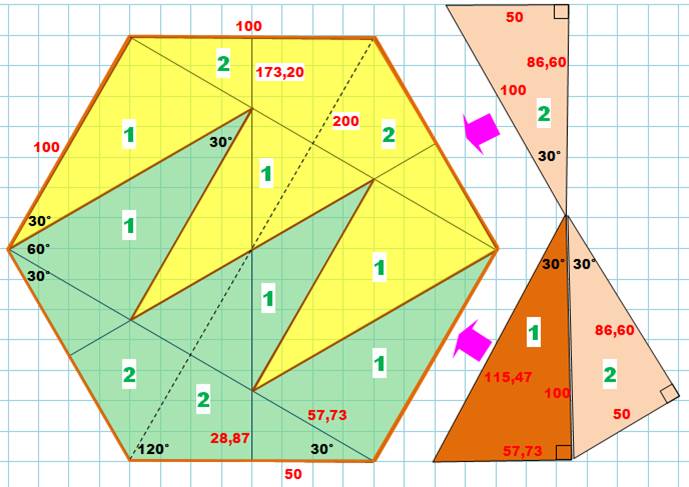
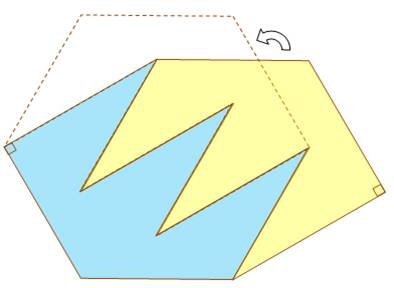
Cette vision donne lieu à une énigme. On donne l’hexagone non-régulier avec ses dimensions (voir données), et on demande de le
rendre régulier tout en conservant la même surface (aire). Données:
La solution consiste à pratiquer les découpes en dents de
scie (cf. figure introductive à ce
chapitre) et à décaler l’un des morceaux (jaune), comme le montre cette illustration en bas. |
|
|||||||||||||
![]()
|
Suite |
|
|
Retour |
|
|
Voir |
|
|
Diconombre |
|
|
Cette page |
http://villemin.gerard.free.fr/GeomLAV/Polygone/Hexagone.htm |
![]()