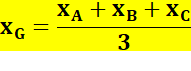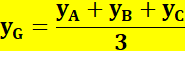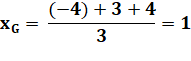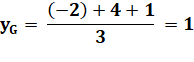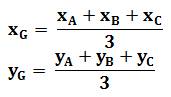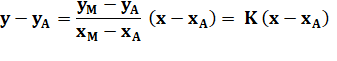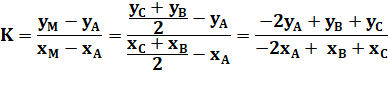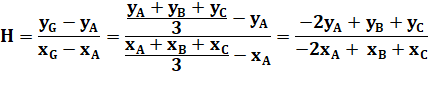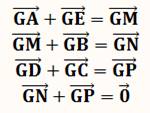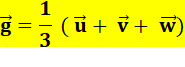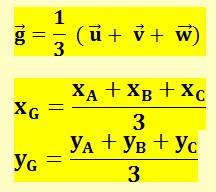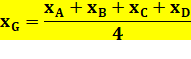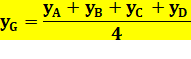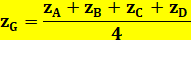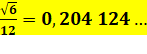|
||||||||||||||||||||||||||||||
![]()
|
Centre gravité du TRIANGLE Centre géométrique, isobarycentre Centre de masse, centre d'inertie Centroid (anglais) Point médian
Nous allons positionner le centre de gravité, énoncer quelques relations
géométriques et, calculer les coordonnées du
centre de gravité. Nous démonterons par la méthode des vecteurs que le ces
coordonnée sont la moyenne
arithmétique des coordonnées des sommets. |
Voir Barycentre – Glossaire
|
|
||
|
Géométrie |
Physique |
|
|
Centre géométrique ou centroïde: moyenne
arithmétique de tous les points d'une figure. Ne pas confondre avec le centre
de la figure. Identique au centre de masse si la figure est
"homogène". Centroid Geometric
center |
Centre de masse ou centre
d'inertie. Identique au centre de gravité si le champ de
gravitation est uniforme. Center of
mass |
|
|
Physique |
Mathématique |
|
|
Centre de gravité: point
d'application de la résultante des forces de gravité ou de pesanteur. Fonction du champ de gravitation. C'est le point d'application du poids. Center of
gravity |
Barycentre: centre de
gravité d'un objet pour lequel chaque point peut être affecté d'un
coefficient de pondération. Généralisation de la notion de centre de gravité. Barycenter |
|
|
Bilan |
||
|
Si tout est simple (matériaux homogène, champ de
gravitation uniforme), tous ces points sont confondus, et on parle le plus
souvent de centre de gravité. Analogie: il est le point où une découpe de la
forme pourrait être parfaitement équilibrée sur la pointe d'une épingle. |
En géométrie pure, les Anglais ont inventé le mot
"centroid", alors que les Français utilisent le mot "centre de
gravité". Le mot "centre géométrique" est peu
usité. Le mot "centroïde" commence à
apparaître. |
|
Centres de
gravité (de masse) du triangle (physique)
|
Surface |
Plaque homogène |
G |
|
Sommets |
Boules identiques |
G |
|
Périmètre |
Tiges homogènes |
Voir Coordonnées
barycentriques
![]()
|
|
||
|
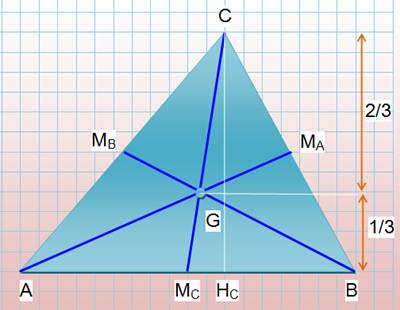
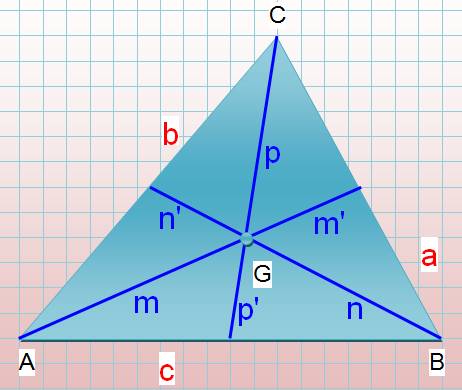
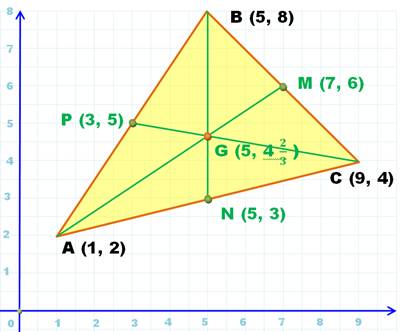
Le centre de gravité (G) du triangle quelconque se
trouve à l'intersection des trois médianes (AMA
, BMB , CMC). Le centre de gravité est
situé au 2/3 de la médiane en partant du sommet. CG = 2/3 CMC En prenant la hauteur issue du même
sommet, celle-ci est partagée également en tiers (théorème de Thalès) |
Le centre de gravité du
triangle est situé au (1/3, 2/3) de la
médiane. |
|
|
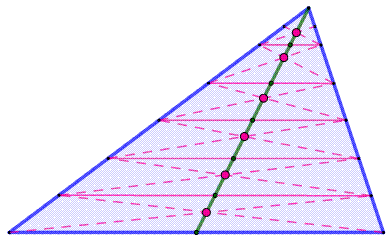
Recherche du centre de gravité Le triangle homogène est découpé en fines bandes
par des droites parallèles à un des côtés. Le centre
géométrique (centroïde) de chaque bande-trapèze (point de concours
des diagonales) est le centre de gravité de la bande. Procédé reconduit pour des bandes de plus en plus
fines, alors la succession des centres de gravité se situent sur une droite
qui est la médiane du triangle. La même méthode reconduite avec les deux autres
côtés engendre les deux autres médianes. Le centré de gravité est leur point de concours. |
Les centres géométriques
des bandes, aussi fines que possible, dessinent la ligne médiane du triangle.
|
|
|
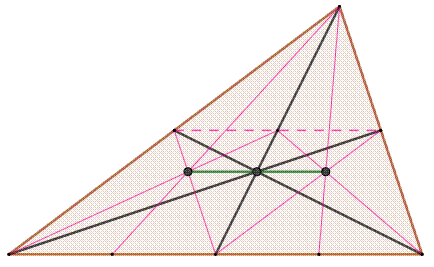
Centre de gravité (autre vision) Chaque médiane partage un triangle en deux triangles
de même aire (car même hauteur et bases de même longueur). Chacun de ces triangles peut également être
partagé en deux par les médianes et produire quatre triangles de même aire. De sorte que le centre de gravité du grand
triangle est la résultante des deux centres de gravité des triangles
latéraux, chacun à égale distance du centre principal (trait vert). Dit-autrement: si le centre
principal est le point d'appui d'une balance, et les plateaux sont les
centres de gravités latéraux. Alors la masse de chacun des triangles
latéraux, placés sur les plateaux, mettront la balance en position
d'équilibre. Ce procédé peut être
renouvelé à loisir en poursuivant le partage en deux de chaque triangle. |
Le centre de gravité du triangle
est le barycentre des centres de gravité des
triangles latéraux. |
|
Suite en Médianes et triangles
Voir Partage du
triangle par une droite et centre de gravité
Merci à JM Allard pour ses remarques
|
Coquin!
Je vous surprends à chercher le point G! |
Voir Pensées & humour
|
|
||
|
Relation cousine de celle du
théorème de Pythagore; Mais celle-ci qui découle du
théorème
d'Apollonius. |
3 (m² + n² + p²)
= a² + b² + c² |
|
|
Théorème d'Apollonius. |
a² + b² – ½ c² = 2 (p +
p')² b² + c² – ½ a² = 2 (m +
m')² c² + a² – ½ b² = 2 (n + n')² |
|
|
Propriété du point de
concours des médianes. |
m + m' = m + ½ m = 3/2 m n + n' = 3/2 n p + p' = 3/2 p |
|
|
En remplaçant: |
a² + b² – ½ c² = 2 (3/2
p)² = 9/2 p² b² + c² – ½ a² = 2 (3/2 m)²
= 9/2 m² c² + a² – ½ b² = 2 (3/2 n)² = 9/2 n² |
|
|
On additionnant tout cela. |
2a² – ½ a² + 2 b² – ½ b²
+ 2c² – 1/2c² = 9/2 (m² n² + p²) |
|
|
Un peu de calcul. |
3/2 (a² + b² + c²) = 9/2
(m² n² + p²) |
|
|
En simplifiant par 3/2. |
a² + b² + c² = 3 (m² n² + p²)
|
|
|
Autre relation pour un point
M quelconque: |
AM²
+ BM² + CM² = AG² + BG² + CG² + 3MG² |
|
|
|
||
|
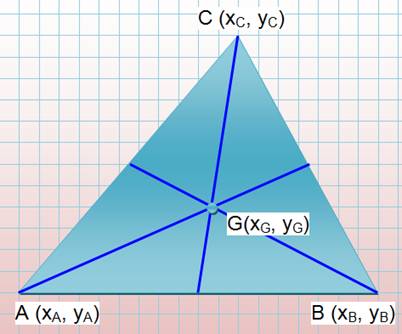
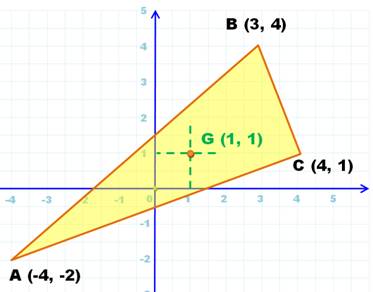
Formule fondamentale Les coordonnées cartésiennes
du centre de gravité du triangle quelconque sont égales à la moyenne arithmétique
des coordonnées des sommets.
|
A (0, 0); B (18, 0); C (11, 12); G(29/3 = 9,66…, 12/3 = 4 ) |
|
|
Exemple
|
|
|
Voir Démonstration
vectorielle de ces relations
|
|
|||
|
Démonstration Montrer que G est aussi le
point de concours des médianes G'. Ce que nous savons:
Nous allons démontrer que AM
et AG sont colinéaires. Démonstration qui peut se
répéter pour les deux autres médianes. Alors G et G' sont confondus. |
AM (médiane) et AG (centre de gravité) |
||
|
L'équation de la droite
AM avec K son coefficient directeur. |
|
||
|
Valeur de K. |
|
||
|
Coefficient directeur de AG. |
|
||
|
Égalité des coefficients
directeurs K et H. |
Les deux droites AG et AM
sont colinéaires et, étant toutes deux issues de A, elles sont confondues. Idem pour BG et BN. Ces droites se coupent au même point G. G et G' représentent le même point. |
||
|
|
||
|
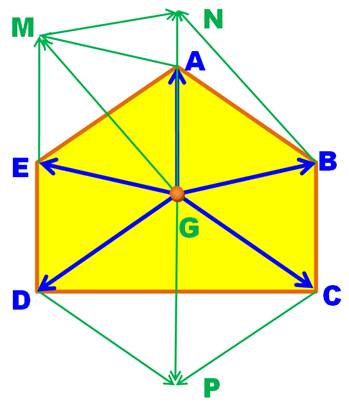
Il s'agit de démontrer que
la somme des vecteurs
issus du centre de gravité et joignant les sommets est nulle (ici, avec l'exemple du triangle). |
Propriétés
vraies pour tous les polygones plans. |
|
|
Coordonnées des vecteurs |
GA = (xA – xG , yA – yG) GB = (xB – xG , yB – yG)
GC = (xC – xG , yC – yG) |
|
|
Somme (S) de ces trois
vecteurs |
xS = xA – xG
+ xB – xG + xC – xG
= xA + xB + xC – 3xG yS = yA – yG
+ yB – yG + yC – yG
= yA + yB + yC – 3yG |
|
|
Or, on connait les
coordonnées du centre de gravité. |
|
|
|
En remplaçant dans la somme
des vecteurs: |
xS = 0 yS = 0 |
|
|
La somme des vecteurs issus de G est égale au: |
vecteur nul. |
|
|
Propriété Le centre de gravité d'un
polygone (plan) est tel que la somme des vecteurs issus de ce point vers
chacun des sommets est nulle.
|
|
|
|
|
|||
|
Démonstration Démontrer la relation
vectorielle associée au centre de gravité.
On sait que le centre du
triangle est aussi le point de concours des médianes, situé au 2/3 des
sommets. La démonstration fait
intervenir la méthode des vecteurs. Nous
allons caractériser les points du triangle par des vecteurs, tous issus de la
même origine quelconque. (On aurait pu choisir G comme point origine. Choix d'une origine
quelconque pour le plaisir d'un calcul vectoriel général). |
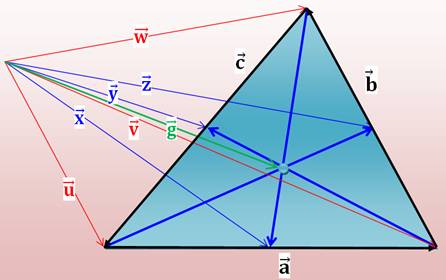
Exemple de relation
Pour alléger l'écriture, nous allons omettre la flèche pour les
vecteurs. |
||
|
Avec les trios (u, v, w) et
(a, b et c). |
a = v – u b = w – v c = u – w |
||
|
Avec le trio (x, y et z)
caractérisant les milieux des côtés. |
x = u
+ ½ a = u + ½ (v – u) = ½ (u + v) y = ½
(u + w) z = ½
(v + w) |
||
|
Les vecteurs sur les médianes. |
ma
= x – w = ½ (u + v) – w mb
= z – u = ½ (v + w) – u mc
= y – v = ½ (u + w) – v |
||
|
En prenant le vecteur g, on
caractérise également des portions de médianes. |
m'a = g – w m'b = g – u m'c = g – v |
||
|
Or les portions de médianes
(ma) et et les médianes (ma') sont colinéaires Les vecteurs sont
proportionnels dans le rapport 2/3. |
ma
= ½ (u + v) – w = 2/3 (g – w) mb
= ½ (v + w) – u = 2/3 (g – u) mc
= ½ (u + w) – v = 2/3 (g – v) |
||
|
En additionnant tout cela,
les termes à gauche s'annulent. |
0 = 2/3 (g – w) + 2/3 (g – u) + 2/3 (g – v) |
||
|
Simplification. |
0 = 3g – u – v – w g = 1/3 (u + v + w)
|
||
|
Formule fondamentale En reprenant la notation
vectorielle. En projetant les vecteurs
sur les axes, les coordonnées cartésiennes du centre de gravité du triangle
quelconque sont égales à la moyenne arithmétique
des coordonnées des sommets. |
|
||
|
|
||
|
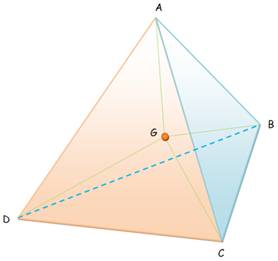
Tétraèdre régulier ou non
Exemple: A (2,
4, 0) B (6,
8, 0) C (8,
-2, 0) D (4,
2, 10) G (5,
3, 2,5) Tétraèdre régulier Distance du centre de gravité à
la base: |
Le centre
géométrique ou centre de gravité se situe à l'intersection des droites
joignant un sommet au centre géométrique de la face opposée. Ces droites sont
les médianes du tétraèdre. Pour tout
tétraèdre, les médianes sont partagées en 1/4, 3/4 par le centre géométrique. Pour le
tétraèdre régulier, AG s'appuie sur la hauteur du tétraèdre et découpe cette
hauteur au 3/4. |
|
|
Centroid of a Triangle: The centroid of a triangle
is kind of the center of the triangle. If you try to balance the triangle on
the tip of your finger, the centroid is where you'll put your finger to keep
it level. A median of a triangle
is a segment joining any vertex to the
midpoint of the opposite side. The medians of a triangle are concurrent. The
intersection of the medians is called the
centroid. The four medians of a
tetrahedron concur in a point that divides each of them in the ratio 1:3, the
longer segment being on the side of the vertex of the tetrahedron |
![]()
|
Suite |
|
|
Voir |
|
|
Aussi |
|
|
Cette page |
http://villemin.gerard.free.fr/aScience/Physique/STATIQUE/Triangle.htm |