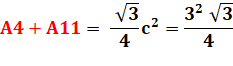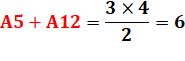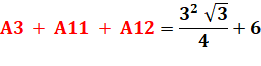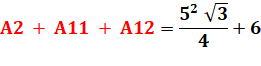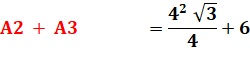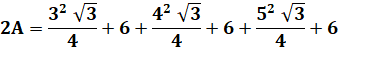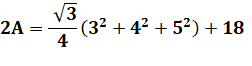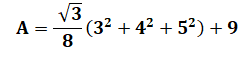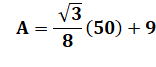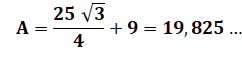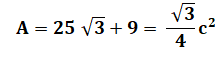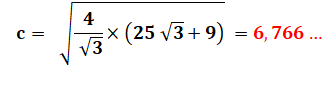NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 29/09/2024 Orientation générale  DicoMot Math Atlas Références M'écrire Barre de recherche DicoCulture Index alphabétique Brèves de Maths
	TRIANGLES
Débutants Triangle	Propriétés – Curiosités				Glossaire Triangle
INDEX Types de triangles Triangle	Point Milieu	Droites et points	Pappus	Point et triangles
	Angles (180°)	Quantité de triangles	Torricelli	Triangles et triangles
		Quatre triangles	Heilbron	Carrés triangles
		Représentation	Brocard	Cercles et triangles
		Équilatéral 345		Démo fallacieuse
		Sommaire de cette page >>> Triangle équilatéral et un point interne >>> Construction pour résolution

TRIANGLE équilatéral

Avec point interne à 3, 4 et 5 des sommets

Plaisant problème de géométrie d'origine indienne qui montre comment calculer la longueur du côté d'un triangle équilatéral en connaissant seulement les distances d'un point à ses sommets. Il est vrai qu'il s'agit d'un cas particulier.

Triangle équilatéral et un point interne
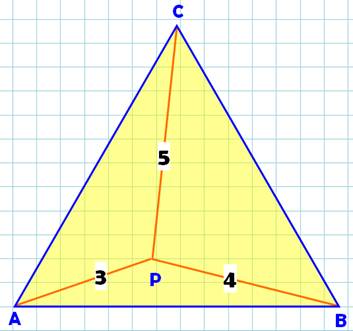
Construction Un triangle équilatéral ABC et un point P, situé à 3, 4 et 5 unités des sommets. Quelle est la longueur des côtés? Commentaires Un problème de géométrie qui semble infaisable, et pourtant … L'idée consiste à raisonner en élargissant le champ, en faisant une construction complémentaire. Avec la présence du triplet de Pythagore (3, 4, 5), une idée vient immédiatement à l'esprit: comment obtenir un triangle rectangle en rapprochant ces trois mesures?	Figure initiale

Construction conduisant à la résolution
Pour calculer la longueur du côté, nous allons d'abord calculer l'aire du triangle équilatéral.
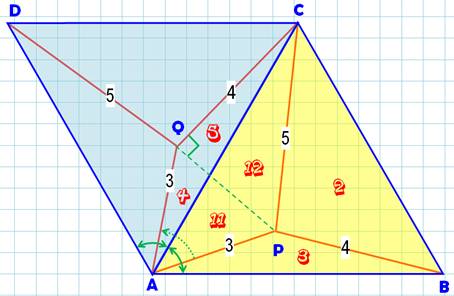
Pistes L'astuce consiste à effectuer une rotation de 60° de l'ensemble de la figure jaune pour l'amener en position bleue. Repérez les angles de 60° marqués en bas à gauche (vert). Les angles des deux triangles équilatéraux, mais aussi l'angle PAQ. Aire du triangle APQ Avec un angle de 60° et deux côtés de même mesure, le triangle APQ est équilatéral: AP = AQ = QP. Son aire est connue:	Figure avec notations et constructions Les nombres en rouge repèrent les surfaces. Ainsi, 2 représente l'aire du triangle BCP. La figure est réalisée à l'échelle: 2 carreaux pour une unité de longueur.
Calcul des aires- relais Le triangle CQP, avec ses côtés en (3, 4, 5), est donc notre fameux triangle rectangle, avec son angle droit en Q.	Aire du triangle rectangle: CQP
Par la rotation le triangle ABP est devenu ACQ.	A3 = A4 + A5
Conséquence: un morceau de la surface à trouver est égal au quadrilatère APCQ.	A3 + A11 + A12 = A4 + A5 + A11 + A12
Or, nous connaissons cette aire: triangle équilatéral APQ et triangle rectangle CPQ.
En recommençant l'opération de rotation sur les deux autres côtés, on trouvera deux autres relations:
Calcul de l'aire du triangle La somme de ces aires couvre deux fois la surface (A) à trouver. Notez que: 3² + 4² + 5² = 50. Bilan C'est évidemment, le triplet de Pythagore qui a été la clé de la solution.
Calcul de la longueur du côté Avec la formule de l'aire du triangle équilatéral, nous pouvons passer au calcul de la longueur du côté.

Championnat

Lors du Championnat International des Jeux Mathématiques et Logiques, Finale Internationale du 23 août 2003, un problème semblable (notamment le n° 15) a été posé: Déterminer l'aire d'une forêt en forme de triangle équilatéral, lorsqu'on se trouve à l'intérieur de cette forêt à des distances de 6,  8 et 10 km des sommets.

Merci à Jos Heynderickx pour cette référence

Retour	Triangle équilatéral
Suite	Triangle isocèle
Voir	Allumettes Carrés Cercle Droite Géométrie – Index Jeux – Index Nombres triangles Polygone Relations dans les triangles Somme de r puissances k Théorème de Pappus Théorème de Pythagore Triangle – Index
Cette page	http://villemin.gerard.free.fr/GeomLAV/Triangle/Particul/Equi345.htm