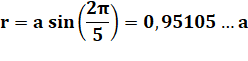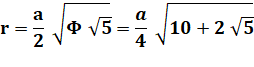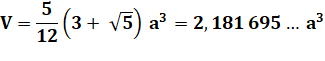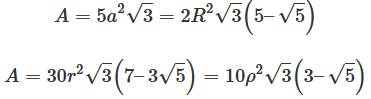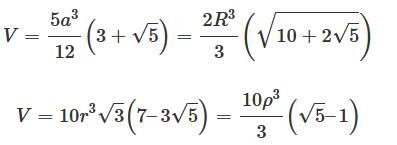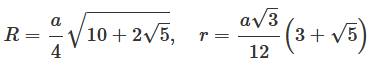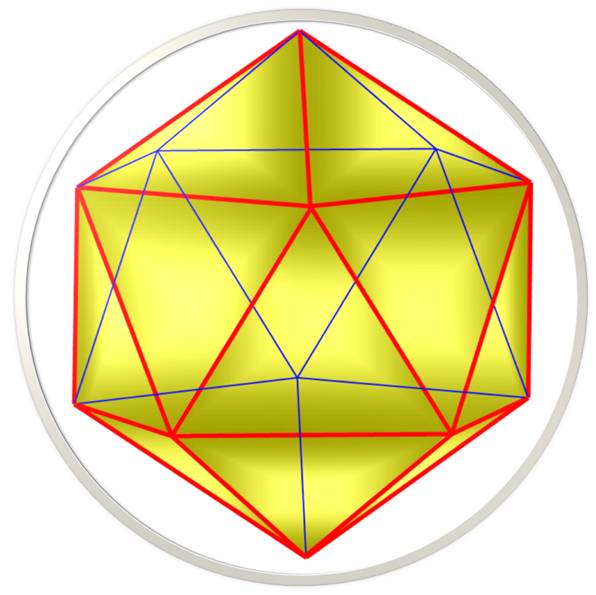
NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 27/04/2022 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Géométrie
Débutants Géométrie	Polyèdres			Glossaire Géométrie
INDEX Géométrie	Polyèdres	Tétraèdre	Cube	Octaèdre
		Dodécaèdre	Icosaèdre
		Sommaire de cette page >>> Représentation >>> À noter >>> Données numériques >>> Dualité >>> Historique >>> Hyper-icosaèdre

Icosaèdre régulier

Polyèdre à vingt faces en forme de triangle équilatéral.

Chacun des douze sommets reçoit cinq faces.

Les vingt triangles ont 3 x 20 = 60 côtés. Chaque côté est partagé par deux faces ; soit 60 / 2 = 30 arêtes.

Connu de Platon; vu dans la nature bien plus tard, en observant les virus au microscope électronique.

Grec eikosaedros (ikosa: vingt, et edros: siège, base) et latin icosahedrum

Anglais: A polyhedron with twenty faces is an icosahedron

Représentation

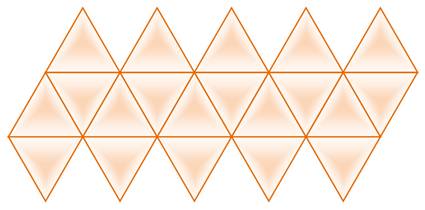
Imaginez trois parties: une pyramide formée de cinq triangles au sommet, pointe vers le haut; une pyramide formée de cinq triangles à la base, pointe vers le bas; et une couronne de dix triangles, cinq dans un sens et cinq dans l'autre, pour associer les deux pyramides. Le patron de l'icosaèdre découle de cette remarque. En plaçant les triangles dans d'autres configurations, il y a 43 380 façons de réaliser le patron de l'icosaèdre. Rappel: il y en a 11 pour le cube.

Anglais: patron net

À noter

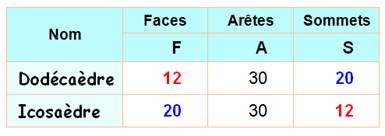
Icosaèdre – Polyèdre à 20 faces – 12 sommets et 30 arêtes. Comme tous les polyèdres, il vérifie la relation: Faces + Sommets – Arêtes = 20 + 12 – 30 = 2 S'il est régulier, ses faces sont des triangles équilatéraux isométriques. C'est le polyèdre régulier qui compte le plus de faces. C'est le dernier des cinq à avoir été découvert. Cinq triangles forment un hexagone. Pas étonnant de retrouver le nombre d'or dans les mesures de l'icosaèdre. Les virus les plus petits sont de forme icosaédrique de 18 à 20 nm de "diamètre".

Icosaèdre – Données numériques
Angle du dièdre
Rayon de la sphère circonscrite
Aire
Volume

Formulaire

a côté A aire V volume R rayon de la sphère circonscrite r rayon de la sphère inscrite rayon de la sphère tangente aux côtés

Dualité
Icosaèdre et dodécaèdre sont duaux. Chacun possède la quantité de faces et de sommets de l'autre, mais croisée. Un pentagone placé sur chacun des 12 sommets de l'icosaèdre forme un dodécaèdre.

Historique

Pythagore (vers – 560) ne connaissait que le tétraèdre (pyramide à base triangulaire), le cube et le dodécaèdre (la sphère des douze pentagones). Théétète, ami de Platon, (vers – 380) comprend qu'il n'est pas possible d'assembler des faces hexagonales pour créer un polyèdre. Seuls les triangles, carrés et pentagones conviennent. Comme pour le dodécaèdre, il pense à prendre deux pyramides ayant quatre faces en triangle équilatéral et une base carrée ayant et à les assembler tête bèche par leur base: c'est l'octaèdre. Puis, avec la pyramide à cinq triangles, il veut appliquer le même procédé. Pour assurer la jonction des deux pyramides, il a l'idée de compléter par des triangles équilatéraux. C'est l'icosaèdre.

Hexacosichoron ou hyper-icosaèdre
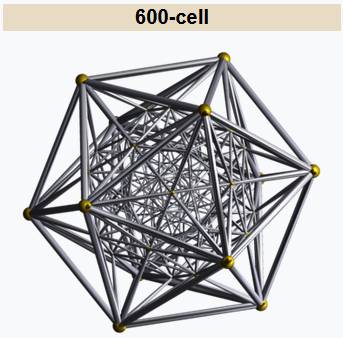
Polytope régulier de dimension 4: 600 cellules tétraèdres réguliers 1200 faces 720 arêtes 120 sommets 7,667 10^308 types de patrons. un des six polychorons réguliers.	Source image Wikipédia

Anglais 600-cell, hexacosohedron, tetraplex

Suite	Voir haut de page
Voir	Polyèdres
DicoNombre	Nombre 20
Site	Icosaèdre – Robert Ferréol Icosahedrom – Mathworld 600-Cell – Wolfram Mathworld HyperSpace, User Manual – Paul Bourke
Cette page	http://villemin.gerard.free.fr/GeomLAV/Objet3D/Icosaedr.htm