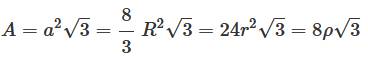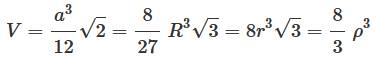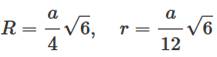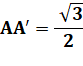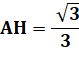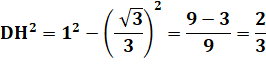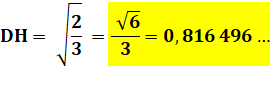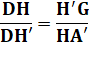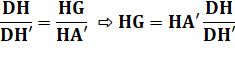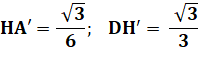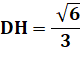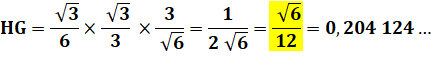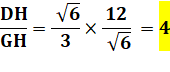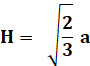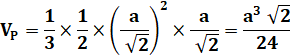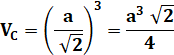|
||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
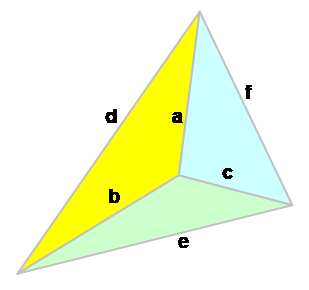
TÉTRAÈDRE
Former quatre triangles équilatéraux identiques avec
six allumettes |
|
a côté A aire V volume R rayon de la sphère circonscrite r rayon de la sphère inscrite
|
|
Voir Pyramide à base carrée – Comparaison avec le tétraèdre
|
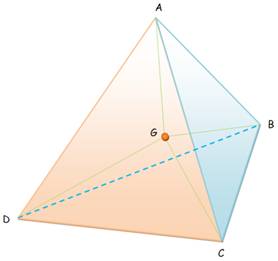
Le diamant est
formé de carbone. Ses atomes occupent les sommets A,
B, C et D de tétraèdres réguliers et leurs centres G. |
Voir
Cristaux
|
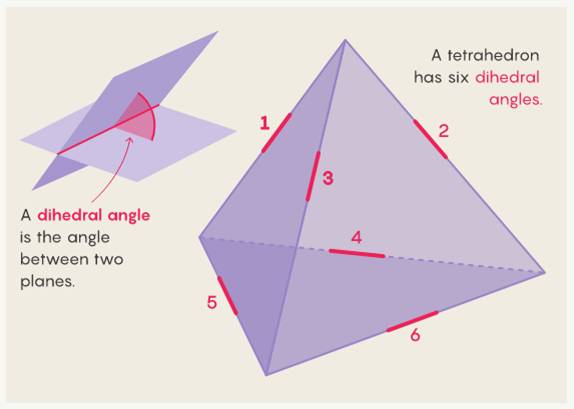
Défi: Il y a 45 ans (1976),
les célèbres mathématiciens britanniques John H. Conway et Antonia J. Jones
lançaient un défi: dresser la liste de tous les tétraèdres dont les angles
sont rationnels, c’est-à-dire qu’ils
peuvent s’écrire sous forme de fraction composée de nombres premiers. Résultat: il existe deux
familles infinies de tétraèdres rationnels et 59 autres tétraèdres isolés.
Cette classification est aujourd’hui complète. Auteurs: Kiran Kedlaya,
Alexander Kolpakov, Bjorn Poonen, Michael Rubinstein Méthode: Les auteurs ont
transformé le problème des six angles en la recherche de six points sur le
cercle unité tels que les nombres
complexes qu'ils représentent soient solutions d'une équation
polynomiale. Les six angles à rendre rationnel
(= fraction)
Source image: Tetrahedron
Solutions Finally Proved Decades After Computer Search – Kevin Hartnett –
Quanta magazine – 2 févier 2021
|
|
|
||
|
Malgré la simplicité des éléments en main, la
solution n'est pas si évidente qu'il y parait. Essayez avant de regarder la
solution. |
|
|
|
|
|
|
Tétraèdre
régulier
|
|
Voir Deltaèdre
|
|
||
|
|
Angle au centre du tétraèdre: 109° 28' Angle entre faces: 70°32' |
|
|
La
distance de la base à G est alors égale à 1/4 ce cette hauteur, soit:
Dans le tétraèdre,
Dans le dodécaèdre,
|
||
|
|
||
|
|
||
|
|
AB
= BC = CA = AD = BD = CD = 1 |
|
|
|
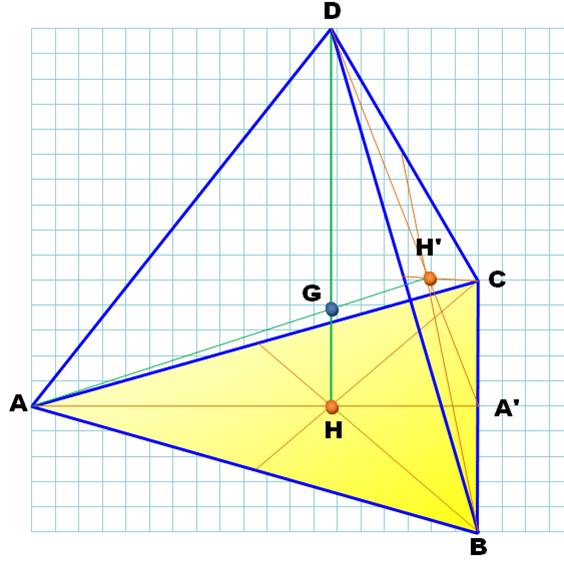
H et H' nous serons utiles. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Rectangles en H et H' Angle commun: HDA' = GDH' |
|
|
|
|
|
|
|
H'G = HG |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
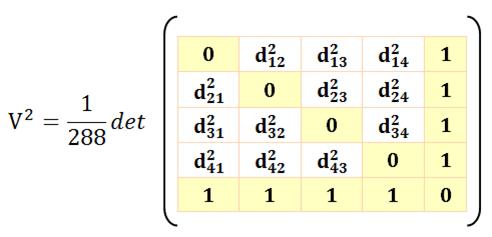
Avec P = 4 a² b² c² Q = a². E² + b². F² + c². D² R = D . E . F D = a² + b² - d² E = b² + c² - e² F = a² + c² - f² |
|
|
|
Voir Démonstration
via le cube |
a = b = c = d = e = f D = E = F = a² P = 4 a6 Q = 3 a6 R = a6 V = 1/12
V = 0,1178511301977579207… a3 |
|
|
|
|
|
|
|
||
|
Le volume d'un tétraèdre couvrant trois
arêtes convergentes d'un parallélépipède est égal au
sixième de celui du parallélépipède >>> |
||
Voir
Exemple de calcul / Volume
via le cube / Aire du triangle
quelconque
|
|
|||
|
Problème
Solution
|
|||
|
|
|||
|
|
Cube en 6 tétraèdres
Cube en 5 tétraèdres
|
||
|
|
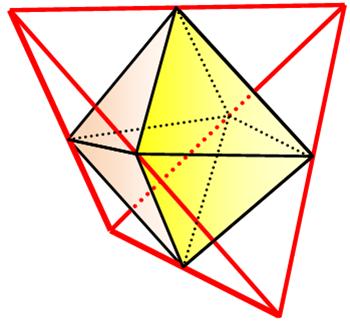
VT = VC – 4 VP |
||
|
|
|
||
|
Volume des tétraèdres latéraux |
|
||
|
Volume du cube |
|
||
|
Volume du tétraèdre central |
|
||
|
|
||
|
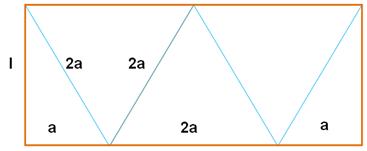
Construction Une
feuille de carton rectangulaire. Enroulée
en cylindre. Pincement
à une extrémité et soudure. Remplissage
avec le produit (lait, shampoing, eau de Javel, …). Idem
de l'autre côté, mais perpendiculairement au premier pincement. Avantages Pas de
chutes de carton. Empilement
possible. Encombrement
réduit |
Brique
tétraédrique ou berlingot
Tetrahedral
package Tetrahedron-shaped
pouch Inventé en 1951 par Ruben Rausing puis
fondation de la société Tetra Pak à Lund en Suède; emballage Tetra Brik®
en 1959. |
|
Voir Brève
871
|
|
||
|
L'octaèdre
complété de quatre tétraèdres sur ses faces non adjacentes créé un tétraèdre
tel que: O(n) + 4T(n-1) = T(2n-1) Exemple
avec les nombres octaédriques et tétraédriqus: O(5) + 4T(4) = T(29) 85 + 4 x 20 = 165 |
|
|
Voir Nombres octaédriques
![]()
|
Suite Tétraèdre |
|
|
Voir |
|
|
Sites |
|
|
Cette page |
![]()
|
|
|
|
|
|