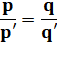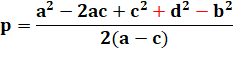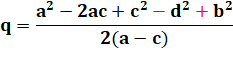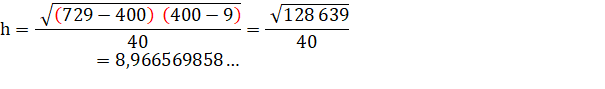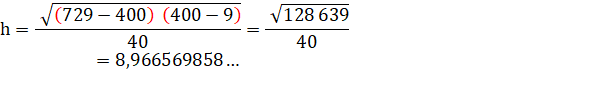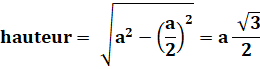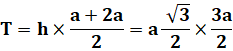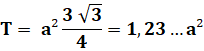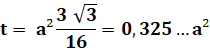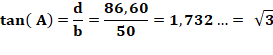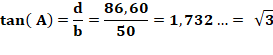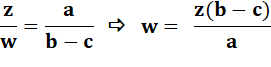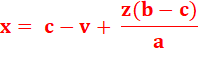|
||||||||||||||||||||||||||||||||||||||||||||||
![]()
ANNONCE: Trapèze des Mascareignes
|
Objet d'un concours en 2020, organisé par les îles Vanilles. Infos sur cette région géographique et sur ce concours >>> |
|
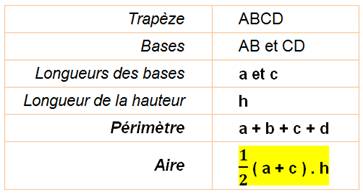
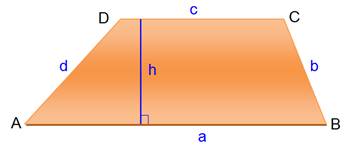
TRAPÈZE Quadrilatère
plan dont deux côtes (exactement) sont parallèles,
appelés bases du trapèze. Un quadrilatère
convexe est un trapèze si et seulement s’il possède une paire d’angles
consécutifs de somme égale à 180° Trapèze isocèle: les deux côtés non parallèles sont de même longueur. Trapèze rectangle: il a un angle droit. |
Américain: Trapezoid / Anglais:
Trapezium
Du grec trapézion: petite table; et
table vient de tetras,
quatre et péza, pied.
|
|
||
|
Aire
Angles A + B + C + D = 360° A + D = B + C = 180° |
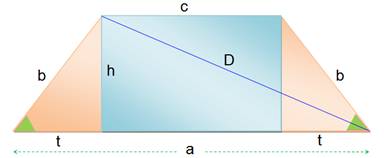
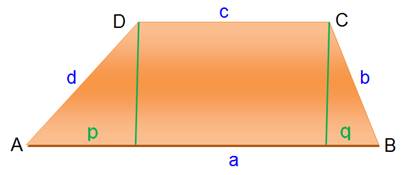
Notation: longueur de AB = a;
etc. |
|
|
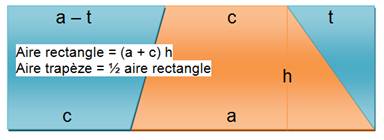
Démonstration géométrique du calcul de l'aire Le trapèze est dupliqué, découpé
puis assemblé à l'original. L'ensemble forme un rectangle contenant deux fois
le trapèze initial. |
|
|
|
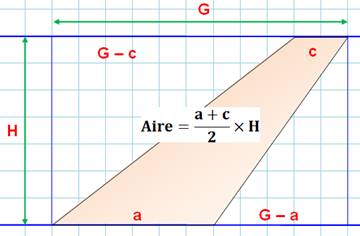
Justification algébrique ATrapèze = ARectangle – T1
– T2 = GH – ½ (G – c)H – ½ (G – a)H = GH – ½ GH + ½ cH – ½ GH + ½ aH = ½ (a + c) H |
|
|
|
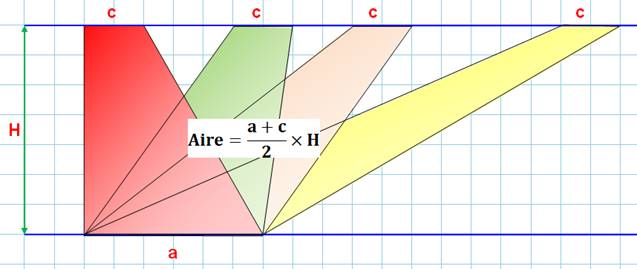
Conséquence Tous ces trapèzes, dont les côtés sont
sur les mêmes parallèles et ont les mêmes dimensions, ont une aire identique.
|
||
Voir Calcul par
intégration de l'aire du trapèze / Calcul analytique de l'aire
du triangle
|
|
||
|
Caractérisation ou condition nécessaire et
suffisante pour qu'un trapèze soit isocèle:
|
||
|
Relations dans le trapèze isocèle Avec un exemple numérique (x veut dire: a priori inconnu)
|
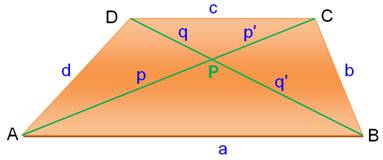
Propriété Un point P dans un trapèze
isocèle de côtés parallèles AB et CD, alors:
Voir Théorème
du drapeau britannique |
|
Voir Triangle isocèle / Centre de gravité du
trapèze isocèle / Trapèze
isocèle en démonstration
|
|
||
|
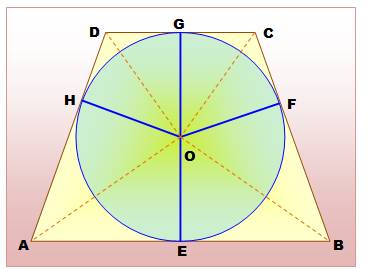
Problème Un cercle
de centre O et de diamètre 10 cm. Un
trapèze isocèle ABCD circonscrit dont l'aire est 100 cm². Donnez la
longueur des côtés AD = BC = x. Solution |
|
|
|
Aire du
trapèze: |
A = ½ EG (AB + CD) = 5 (AB + CD) |
|
|
Avec les
triangles marqués par les pointillés, égaux deux à deux (angle droit, côté
commun et côtés égaux à R). |
AB + CD = AE + EB + DG + GC =
AH + BF + HD + FC = AD + BC |
|
|
En
remplaçant: |
A
= 100 = 5 (AD + BC) = 5 . 2x x = 10 cm |
|
|
Si AD =
BC = EG = 10 cm, alors: |
ABCD est un carré de 10 cm de
côté et son aire est bien 100 cm². |
|
|
|
||
|
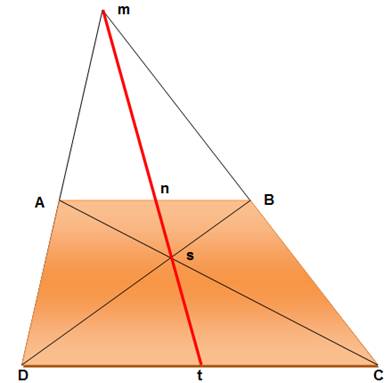
Théorème Les quatre points m,
n, s, et t liés au trapèze sont alignés. Démonstration |
|
|
|
Homothétie de centre |
s |
|
|
avec les parallèles |
AB et DC |
|
|
L'image de |
A
étant C |
|
|
Celle de |
B
est D |
|
|
Globalement |
AB
devient CD |
|
|
Leurs milieux sont
aussi homothétiques |
n
devient t |
|
|
Et alignés sur le
centre d'homothétie |
n,
s et t sont alignés |
|
|
Homothétie de
centre |
m |
|
|
avec les parallèles |
AB et DC |
|
|
Globalement |
AB
devient DC |
|
|
Leurs milieux sont
aussi homothétiques |
n
devient t |
|
|
Et alignés sur le
centre d'homothétie |
n,
m et t sont alignés |
|
|
Bilan |
n, m, s et t sont alignés |
|
|
|
||
|
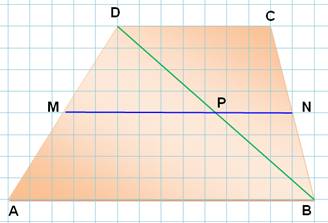
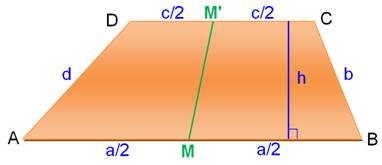
Première médiane
MN est parallèle aux bases
AB et CD. MN = ½ (AB + CD)
MP = ½ AB et PN = ½ CD
|
English: The median of a trapezoid is parallel to
the bases and equal to one-half the sum of the bases. |
|
|
|
||
|
Seconde médiane
|
|
|
|
|
|
|
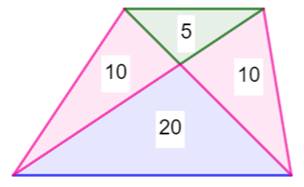
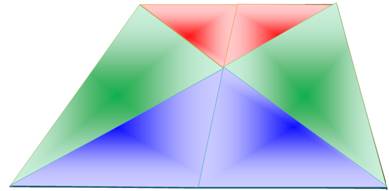
Voir Médiane
À retenir:
les deux triangles latéraux ont la même aire
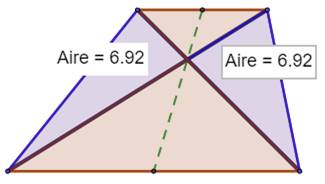
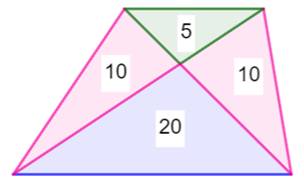
Produit des aires
roses = produit de l'aire verte par
l'aire bleue
Voir Brève 55-1088
|
|
||
|
Relation entre diagonale P et Q et les côtés P²
+ Q² = 2ac + b² + d² Avec P = p + p' et Q = q + q' |
|
|
|
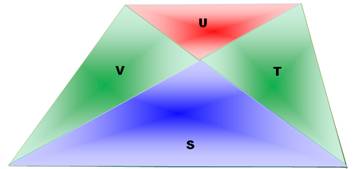
(V + U) (S + T) = (V + S) (U + T)
VS + VT + US
+ UT = VU + VT + SU
+ ST VS + UT = VU + ST V (S – U) = T (S – U) (V – T) (S – U) = 0
|
|
|
Voir Généralisation au quadrilatère
convexe quelconque
|
|
||
|
|
|
|
|
Exemple numérique
|
|
|
|
|
||
|
|
||
|
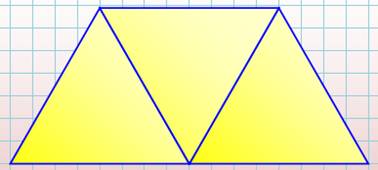
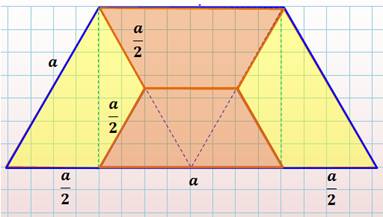
La découpe du trapèze La figure montre la découpe de ce trapèze
isocèle en trois triangles
équilatéraux identiques. Comment le découper en quatre pièces
identiques ? Réponse Deux solutions (exposées ci-dessous) avec quatre trapèzes. |
|
|
|
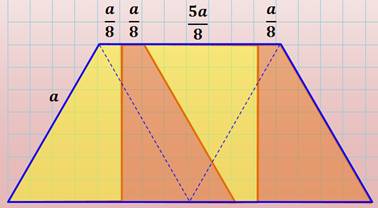
Première possibilité Quatre trapèzes rectangles (a, a/8, h,
a/2), avec :
|
|
|
|
Deuxième possibilité Quatre trapèzes isocèles (a, a/2, a/2,
a/2). Ces quatre pièces et les quatre précédentes
ont la même aire (t)
|
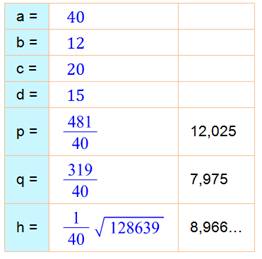
Aire
du grand trapèze : 1,23 x 8² = 83,14... (Vérification
en comptant les carreaux ; 12 x 7 = 84). |
|
Trapèzes
bovins

|
|
||||
|
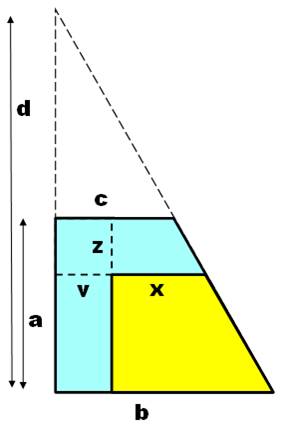
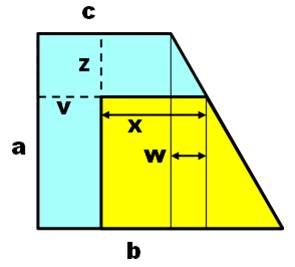
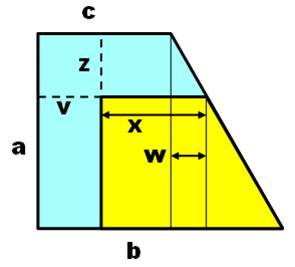
Problème Un
trapèze bleu dont on connait les dimensions a, b et c. On réduit
ce trapèze pour obtenir le trapèze jaune en raccourcissant les bases et la
hauteur de la même quantité z. Quelle
est la valeur de la longueur x de la nouvelle base du haut ? Indice Non, les deux trapèzes ne sont pas homothétiques
(semblables). Les dimensions n'ont pas été réduites dans les
mêmes proportions. On a retranché une valeur donnée dans les deux directions.
Valeurs identiques, certes, mais il s'agit d'une soustraction et non pas une
division. Solution (triangle rectangle
externe) La solution passe par le tracé du triangle
rectangle prolongeant le trapèze bleu; en introduisant la hauteur dont il est
facile de calculer la longueur en appliquant le théorème de
Thalès. |
|
|||
|
Avec les triangles semblables impliquant le
trapèze bleu: |
|
|
||
|
On en déduit la valeur de d: |
|
|||
|
Avec les triangles semblables impliquant le
trapèze jaune: |
|
|
||
|
En arrangeant: |
|
|||
|
Exemple numérique Données Trapèze bleu: a = 60 b = 50 c = 15,36 Trapèze jaune z = 10 et v = 10 Calcul
Note L'angle à la base n'a pas d'importance. Il est
d'ailleurs imposé par la taille du trapèze bleu. Ici, l'angle vaut
60° et sa tangente, racine de 3.
|
|
|||
|
Méthode équivalente (triangle
rectangle interne)
Application numérique |
|
|||
|
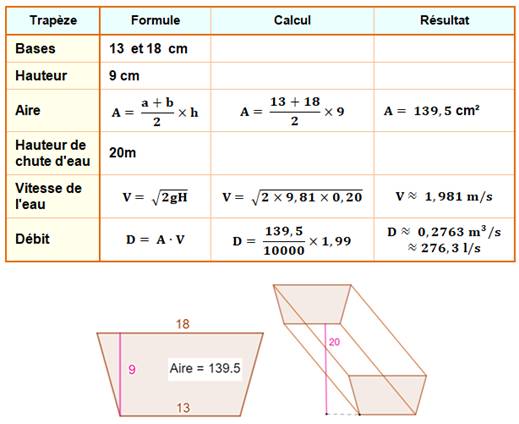
Données La section de la canalisation est
trapézoïdale. Bases: 13 et 18 cm; hauteur: 9cm. La canalisation depuis sont point
haut à son point bas correspond à une hauteur de 20 m. Calculs Voir le tableau qui indique les
formules de calcul. Avec ces données, le débit est de 276
litres par secondes. |
|
||
|
Programme Python import math # Données a_cm = 13 # petite base en cm b_cm = 18 # grande base en cm h_cm = 9 # hauteur du trapèze en cm H_m = 20 # hauteur de chute en mètres g = 9.81 # accélération gravitationnelle en m/s² # Conversion en mètres a = a_cm / 100 b = b_cm / 100 h = h_cm / 100 # Calcul de la section trapézoïdale
(en m²) section = ((a + b) / 2) * h # Calcul de la vitesse théorique
(en m/s) vitesse = math.sqrt(2 * g * H_m) # Calcul du débit (en m³/s) debit = section * vitesse # Affichage des résultats print(f"Section trapézoïdale :
{section:.4f}
m²") print(f"Vitesse théorique : {vitesse:.2f} m/s") print(f"Débit théorique : {debit:.4f} m³/s ({debit * 1000:.1f} L/s)") Résultats Section trapézoïdale : 0.0139 m² Vitesse théorique : 19.81 m/s Débit théorique : 0.2763 m³/s (276.3 L/s) |
But Calculer le débit d'une canalisation de
section trapézoïdale. Commentaires Programme simple qui suit rigoureusement la
disposition utilisée dans le tableau. |
||
Voir Programmation – Index / Programmes Python – Index
![]()
|
Suite |
|
|
Voir |
|
|
DicoNombre |
|
|
Site |
|
|
Cette page |
![]()