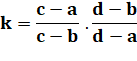|
|||||||||||||||||||||||||||||||||||
|
Triangles
HOMOLOGIQUES - Idée Construire des triangles jumeaux (homologues)
dont les sommets deux à deux se trouvent sur des droites concourantes
en un seul point. |
|
|
||
|
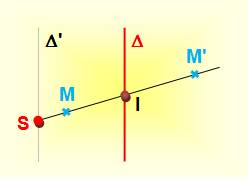
Transformation plane
de centre (sommet ou
pôle) S d'axe de birapport k. - On trace parallèle à -
Soit un point M non situé sur et son image M' SM coupe L'homologie est telle que le birapport
des points (S, I, M, M') est égal à k. Dans le cas où k = - 1, l'homologie est dite harmonique. |
Birapport (k) ou rapport anharmonique de quatre
points alignés d'abscisse a, b, c, d
|
|
Voir Birapport
|
|
||
|
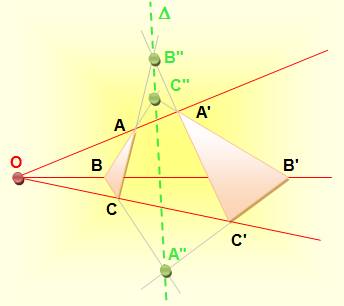
Construction Les triangles ABC et A'B'C', tels que
les droites AA', BB' et CC' sont toutes trois concourantes en O, sont deux
triangles homologiques. Propriétés -
Théorème de Desargues 1.
Les cotés prolongés des deux triangles se coupent deux à deux
en A", B" et C" et ces trois points sont alignés, portés par
la droite 2.
Il existe
une homologie transformant le triangle A en triangle A'B'C' de centre O et
d'axe La
réciproque de ce théorème est vraie. |
|
|
|
Site |
|
|
Voir |
|
|
Cette
page |
