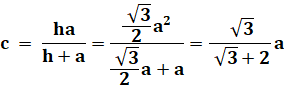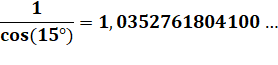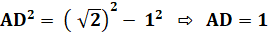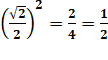NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 20/12/2024 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	TRIANGLES
Débutants Triangle	Propriétés – Curiosités				Glossaire Triangle
INDEX Types de triangles Triangle	Point Milieu	Droites et points	Pappus	Point et triangles
	Angles (180°)	Quantité de triangles	Torricelli	Triangles et triangles
	Médianes	Quatre triangles	Heilbron	Carrés & triangles
	Trois carrés	Représentation	Brocard	Carrés & trg. rectangle
	Démo fallacieuse	Équilatéral 345		Cercles et triangles
		Sommaire de cette page >>> Triangle rectangle dans un carré >>> Problème du carré dans un triangle >>> Calculs >>> Valeurs >>> Cas du triangle équilatéral >>> Problème du triangle maximum dans un carré >>> Problème du carré maximum dans triangle >>> Problème du triangle minimum

CARRÉS et TRIANGLES

1) Aire du carré inscrit dans un triangle isocèle?

Exemple de calcul simple mais qui mérite attention.

Ne pas se perdre dans les facteurs 2, par exemple! >>>

2) Quelle est la taille maximale d'un triangle

positionné à l'intérieur d'un carré?

Ne pas s'embarquer dans des calculs compliqués! >>>

3) Un carré d'aire maximale dans un triangle à choisir

mais d'aire unitaire >>>

4) Un triangle d'aire minimale dans un repère >>>

Anglais: Largest inscribed square

Triangle rectangle dans un carré		haut
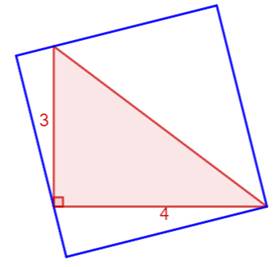
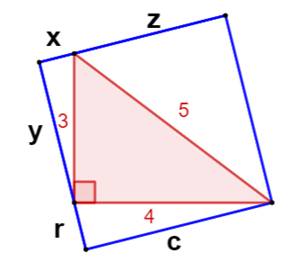
Construction Un triangle rectangle de côtés 3 et 4. Un carré circonscrit. Quelle est la longueur du côté ? Résoudre toute cette figure. Pistes Nous avons reconnu le célèbre triangle rectangle 3, 4, 5. Les deux petits triangles d'hypoténuse 3 et 4 sont semblables car leurs angles sont égaux deux à deux. Un calcul de proportions et un peu de Pythagore vont suffire. 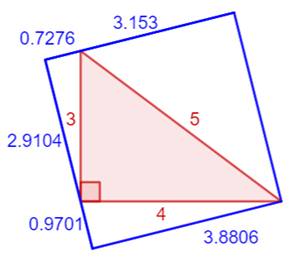Calculs	Figure initiale Notations Vérification avec GeoGebra

Voir Défis en géométrie – Index

Problème du carré dans un triangle isocèle
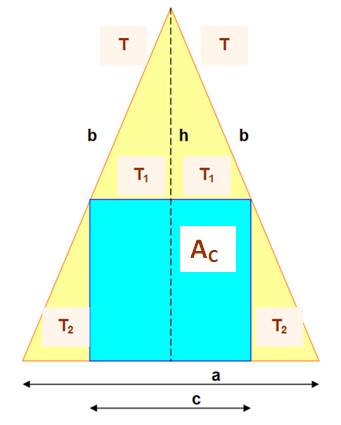
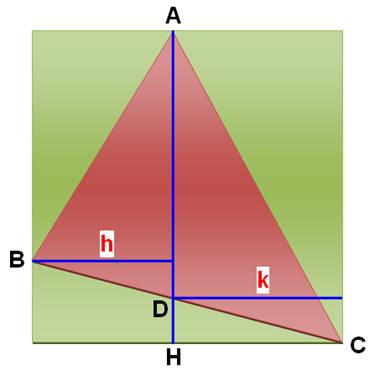
Données Un triangle isocèle - base de longueur a - côtés de longueur b - hauteur h - aire totale = 2T = aire des deux triangles rectangles Un carré inscrit - côté de longueur c - aire Ac Le carré dans le triangle découpe - un triangle en haut formé de deux triangles rectangle d'aire T1 - deux triangles rectangles en bas d'aire T2	Figure
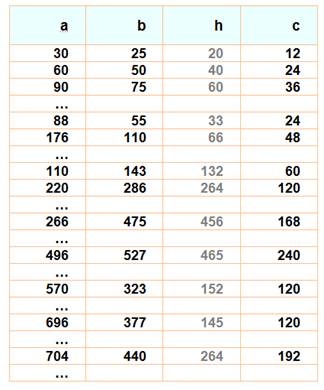
Problème Connaissant les longueurs a et b des côtés du triangle, trouvez la longueur c du côté du carré inscrit.	Principe du calcul Il consiste à égaler l'aire du grand triangle à la somme des aires des figures qui le compose: le carré et les 2 x 2 triangles rectangles.
Ce problème fait partie de l'héritage arabe. Il a été décrit par le célèbre mathématicien Al-Khwarizmi (780-850). Cité par Ahmed Djebbar – L'algèbre arabe, genèse d'un art - Vuibert

Merci à Gilbert Bosmans

Calculs
Étapes calcul	Littéral	Numérique a = 60 ; b = 50
Calcul de la longueur de la hauteur (Pythagore)	h² = b² – (a/2)²	h² = 50² – 30² = 1600 h = 40
Aire du grand triangle isocèle	2T = ½ h x a = ha/2	2T = ½ x 40 x 60 = 1200
Aire triangles du haut	2T1 = ½ (h – c) x c = hc/2 – c²/2	2T1 = 20c – c²/2
Aire triangles du bas	2T2 = 2 { ½ c x (a/2 –c/2) } =ac/2 – c²/2	2T2 = 30c – c²/2
Aire du carré	Ca = c²
Égalité des aires	2 T = Ca + 2T1 + 2T2 ha/2 = c² + hc/2 – c²/2 + ac/2 – c²/2 ha/2 = hc/2 + ac/2 ha = hc + ac	1200 = c² + 20c – c²/2 + 30c – c²/2 1200 = 20c + 30c = 50 c c = 1200 / 50 = 24
Résultat		c = 40 x 60 / (40 + 60) = 24

Valeurs entières
Les valeurs entières jusqu'à a < 1000 b < 1000 Les multiples sont indiqués pour les premières valeurs.

Cas du triangle équilatéral
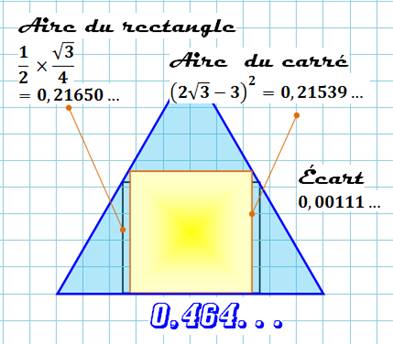
Le plus grand carré dans le triangle équilatéral de notre formule au triangle équilatéral Avec la hauteur h = /2 a Comparaison Le rectangle construit à partir des perpendiculaires issues des points milieux de deux côtés conduit à une aire très proche du maximum. L'écart est seulement de 0,001, soit 5 ‰.
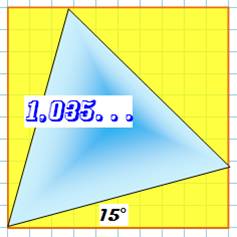
Le plus grand triangle équilatéral dans le carré C'est un triangle incliné de 15° et dont le côté mesure: Et l'aire: Note:

Voir Angle de 15°

Le triangle max. dans un carré
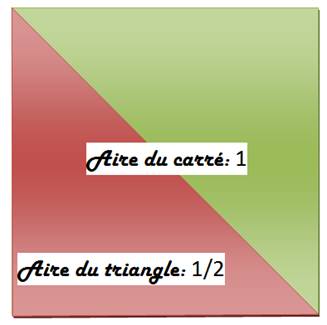
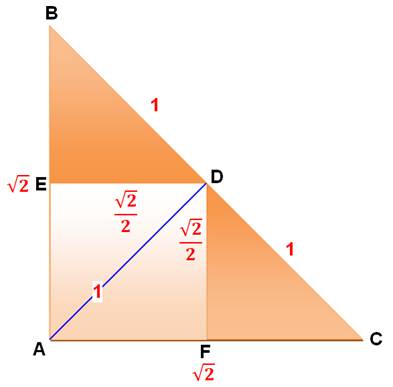
Nous disposons d'un carré unité, quelle est l'aire maximale du triangle logé dans ce carré? Une première idée consiste à dessiner le triangle rectangle et isocèle avec ses trois sommets communs à trois sommets du carré. Son aire est égale à la moitié de celle du carré. Est-ce le maximum? La réponse est oui! Note: le plus grand carré dans un triangle d'aire unité est un problème qui n'a pas de sens. Dans un triangle très effilé, il n'y aurait même pas la place pour un tout petit carré. >>>	L'aire du triangle est le demi-produit des longueurs de d'un côté et de la hauteur attenante.
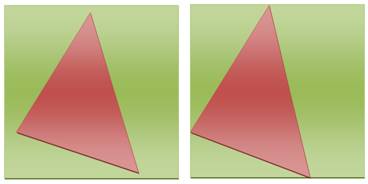
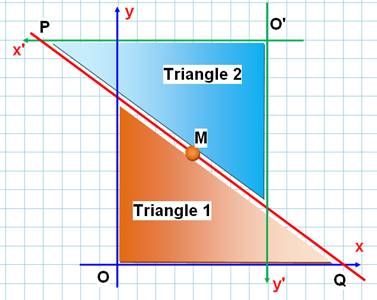
Cas de gauche: tout triangle dessiné à l'intérieur sera toujours plus petit qu'un triangle inscrit. Il suffit de le faire grossir par homothétie (zoom) pour toucher l'un des côtés du carré. Cas de droite: le triangle est inscrit, ses sommets sont situés sur les côtés du carré. Il suffit de faire glisser l'un des sommets vers un sommet du carré pour faire grossir le triangle. Cas du bas: Considérons le cas du triangle inscrit donc un sommet est commun avec le carré. Pouvons-nous le faire grossir au-delà du demi-carré?	L'aire du triangle grandit lorsqu'on plaque ses sommets sur les côtés du carré, et même plus si l'un des sommets est sur un sommet du carré.
Partageons le carré, et par là même le triangle en deux par AH. Aire de ABD = ½ AD . h Aire de ACD = ½ AD . k Aire de ABC = ½ AD . (h + k) = AD L'aire du triangle ABC est maximale si la longueur AD est maximale et égale à 1.
Dans ce cas, D est en H et B est sur le sommet du carré. L'aire du triangle est égale à la moitié de celle du carré. Ce qui constitue un maximum.

Carré max. dans triangle unité
Ici nous considérons un triangle d'aire unité à notre convenance pour qu'il accommode le plus grand carré possible. Quelle est la forme du triangle? On montre qu'il s'agit de la figure ci-contre: triangle rectangle isocèle de mesure: carré logé dans l'angle droit. Calculs Aire triangle: 2 x ½ x 1 x 1 = 1 Aire du carré:	Cette configuration maximalise l'aire du carré (1/2) pour un triangle à choisir d'aire unité. La démonstration n'est pas simple.

Triangle minimum
Un système d'axes (O,x,y) et un point M. trouvez quelle est la droite PQ passant par M qui minimise l'aire du triangle 1. La solution consiste à dessiner l'image miroir: système d'axes (O', x', y') qui met en évidence le triangle 2, de même aire que le triangle 1. Avec les deux petits triangles qui dépassent sur les côtés, l'aire sommée des deux triangles dépasse toujours celle du rectangle. Le seul cas où cette aire est égale à celle du rectangle (et pas possible d'obtenir moins moins) est le cas où PQ est la diagonale du rectangle Alors, l'aire minimale est moitié de celle du rectangle.

Voir	Allumettes Angle Arbres de distribution Carré dans le triangle, construction astucieuse Carrés Cercle DicoMot Droite Éléments de géométrie Géométrie Nombres triangles Polygone Relations dans les triangles Somme de r puissances k Triangle de Calabi et ses trois carrés dans le triangle Triangles Triangles – Types Trigonométrie
Livre	Problems for mathematicians young and old by Paul Halmos – The Mathematical Association of America.
Cette page	http://villemin.gerard.free.fr/GeomLAV/Triangle/Particul/Carretrg.htm