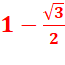|
|||||||||||||||||||||||||||||||||||||||||||||
Faites
un double-clic pour un retour en haut de
page
![]()
|
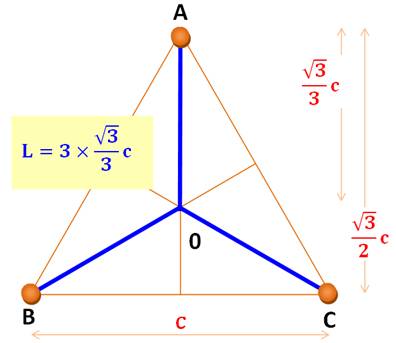
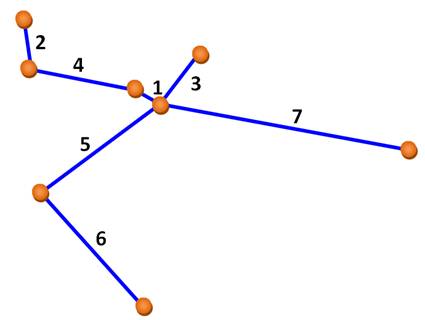
ARBRE DE DISTRIBUTION Problème de l'arbre de Steiner Problème d'optimisation combinatoire. Applications: conception de réseaux, circuits électroniques,
réseaux routiers, arbres phylogénétiques. Ce problème est proche du problème de l'arbre couvrant
minimal. Il est difficile de donner une solution exacte du problème de
Steiner car il est NP-complet.
Toutefois, il existe des algorithmes
approximatifs très performants. |
Anglais: Steiner tree
problem, minimum Steiner tree problem
Historique
|
Les origines du
problème de Steiner remontent au XVIIème siècle. Le mathématicien français
Pierre de Fermat
se demanda comment trouver un point P dans un triangle
de manière à ce que la longueur totale des arêtes concourantes au point P
soit la plus petite possible. Le problème de
Steiner, nommé en référence à Jakob Steiner
(1796-1863, mathématicien suisse), est la généralisation de cette question.
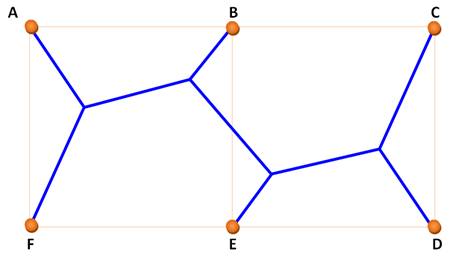
Étant donné un ensemble S de points, il s’agit de trouver l’arbre reliant
tous les sommets de S tel que sa longueur soit minimale. |
|
|
||
|
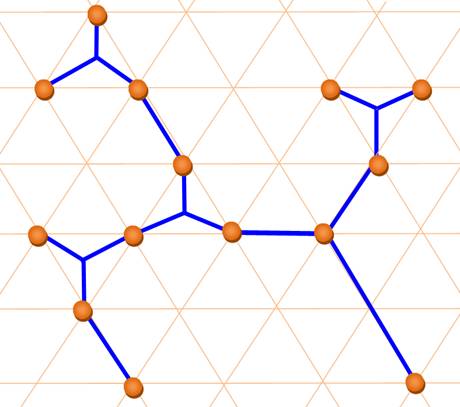
Conjecture de Steiner Entre
un arbre de distribution directe et l'arbre optimisé, le maximum de gain en
longueur est 13,4%. |
Rapport de Steiner |
|
|
Compte
tenu de la difficulté pour trouver l'optimum en longueur de ce réseau et du
faible gain attendu, les constructeurs de réseaux se contentent de l'arbre direct ou
optimisé localement. |
|
|
Voir Arbres
en général – Introduction, types / Problème
d'optimisation d'un réseau (de la voierie entre maisons)
|
|
||
|
|
|
|
|
|
||
|
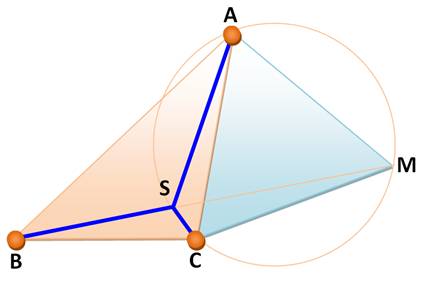
dessinez le triangle
équilatéral ACM et son cercle circonscrit.
|
|
|
Voir Point de Torricelli et
point de Fermat
|
|
||
|
|
|
|
|
|
||
|
|
|
|
Voir Algorithme
/ Algorithme glouton pour la
coloration de graphes
|
|
||
|
|
|
|
![]()
|
Suite |
|
|
|
Voir |
|
|
|
Sites |
|
|
|
Cette page |
||
![]()
Pour mémoire: copie de la page datant
de la fin des années 1980 lorsque ce site n'existait que sous forme de document
papier
Première mise en ligne
Internet en 1998

![]()