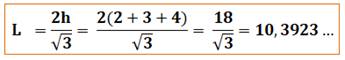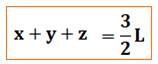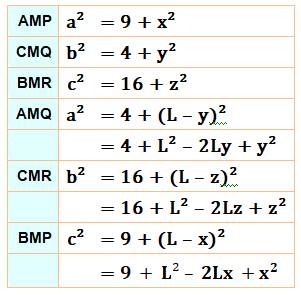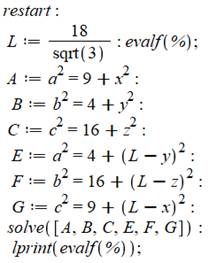NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 21/01/2024 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	TRIANGLES
Débutants Triangle	Types de TRIANGLES					Glossaire Triangle
INDEX Triangle équilatéral Triangle Géométrie	Types	Rectangle		Équilatéral (1/3)	Équilatéral – Construction
	Quelconque	Isocèle		Équilatéral (2/3)	Équilatéral – Curiosités
				Équilatéral (3/3)	Équilatéral – Entier
					Carré et 2 Trg Équilatéraux
			Sommaire de cette page >>> Théorème de Viviani >>> Généralisation aux polygones >>> Résolution d'un cas "Viviani"

TRIANGLE ÉQUILATÉRAL (3/3)

Théorème de Viviani et applications

Propriétés générales en première partie.

Propriétés spécifiques en deuxième partie.

Théorème de Viviani en troisième partie.

Théorème de Viviani
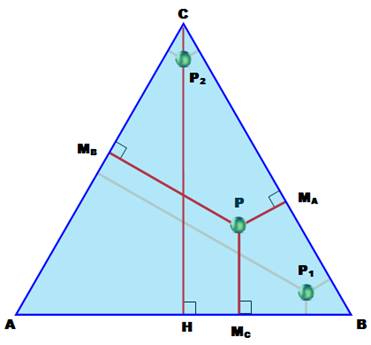
Théorème Dans un triangle équilatéral, la somme des distances d'un point intérieur quelconque aux côtés est égale à la longueur de la hauteur. PMA+ PMB + PMC = CH = AB Démonstration Somme des aires de triangles: AABC =AAPB + ABPC + ACPA ½ (a.h) = ½ (a.h1 + a.h2 + a.h3) h = h1 + h2 + h3 Note: propriété évidente pour P en C, A ou B.	Propriété remarquable qui se démontre très simplement avec le calcul des aires.

Généralisation aux polygones réguliers
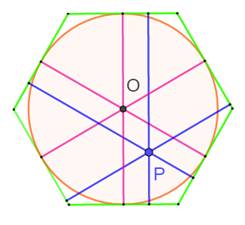
Généralisation Théorème Dans un polygone régulier, la somme des distances d'un point intérieur quelconque aux côtés, est constante; c'est celle obtenue en plaçant le point au centre du cercle inscrit. Cette somme vaut n fois la longueur de l'apothème (= rayon du cercle inscrit). Exemple pour l'hexagone (figure): la longueur totale des six traits bleus issus de P est égale à la somme des longueurs de six rayons rouges du cercle inscrit (O). 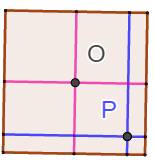Note: chacun des six traits bleus, perpendiculaire au côté, représente la distance du point P au côté correspondant. Carré: la somme des longueurs, de manière évidente, est égale à deux fois la longueur du côté. Parallélogramme: la propriété est valable pour les parallélogrammes et tous les polygones à nombre pair de côtés, parallèles deux à deux.	Cas de l'hexagone En termes de longueurs: somme bleue = somme rouge pour tout point P interne à l'hexagone. Propriété évidente pour le carré

Résolution d'un cas "Viviani"
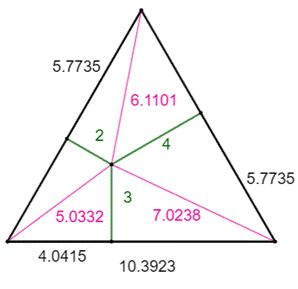
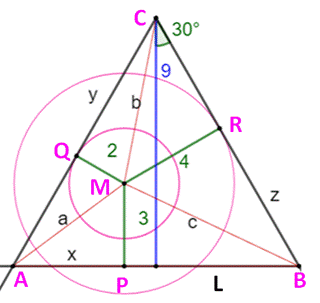
But Construire le triangle équilatéral connaissant les distances d'un point aux trois côtés. Exemple Dans le triangle équilatéral le point interne se situe à 2, 3 et 4 cm des côtés. Quelle est la longueur L du côté et la valeur de x permettant la construction de la figure ? Construction Tracer un triangle équilatéral ABC de côté L. Porter la longueur x sur un côté (AP), puis tracer la perpendiculaire de 3 cm en P à AB. Du point M, perpendiculaires en M aux deux autres côté (Q et R). Avec L et x déterminés, alors MQ = 2 et MR = 4. Calcul de L et de x Les triangles rectangles comme AMP et AMQ permettent d'établir six équations pour six inconnues. Sont connus: MP = 3, MQ = 2 et MR = 4; mais aussi la hauteur (théorème de Viviani) égale à 9 cm. Alors, le côté du triangle s'en déduit: Pour information	Figure et notations Équations (Théorème de Pythagore)
Résolution avec logiciel de calcul (Maple)	Illustration de la solution (GeoGebra)

Retour	Triangle équilatéral – Première partie Cercles et triangle équilatéral
Voir	Allumettes Égalités des triangles Jeux Polygones Résolution du triangle quelconque Triangle de Pythagore Types de triangles
Sites	Théorème de Viviani – Wikipédia Encyclopedia of triangle centers – Clark Kimberling's Viviani's Theorem – Cut-the-knot - Animation
Cette page	http://villemin.gerard.free.fr/GeomLAV/Triangle/Types/TrgequiV.htm