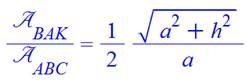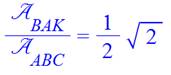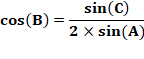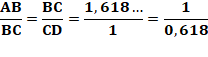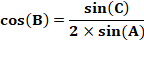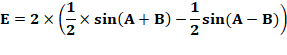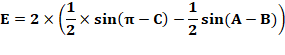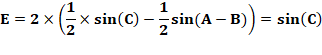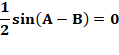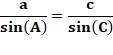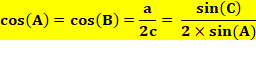Triangle isocèle

NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 01/04/2022 Orientation générale DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	TRIANGLES
Débutants Triangle	Types de TRIANGLES			Glossaire Triangle
INDEX TRIANGLE	Général	Triangle isocèle
	Types	Débutant	Isocèle de 45° au sommet
	Quelconque	Développements	Isocèle – Intersections
	Rectangle	Propriétés	Isocèle – Bissection
	Équilatéral	Résolution	Isocèle – Construction
		Sept triangles isocèles	Isocèle – 20 80 80
			Isocèle – 36 72 72
		Sommaire de cette page >>> La rosace isocèle? >>> Triangle isocèle >>> Triangle isocèle dans triangle isocèle >>> Triangle isocèle-rectangle >>> Triangles en proportions >>> Côtés sont égaux => angles égaux – Démonstration >>> Triangle isocèle 30-30-120 >>> Triangle d'or >>> Aire du triangle isocèle >>> Isocèle en trigonométrie >>> English corner >>> Problème du billard d'Alhazen

TRIANGLE ISOCÈLE

Développements

Triangle qui a deux côtés égaux; ou deux angles égaux (triangle isoangle)

Avec trois côtés (ou trois angles) égaux, le triangle est équilatéral.

Orientation

Initiation, débutants, voir Triangle isocèle, approche

Développements sur le triangle isocèle, voir cette page

Le formulaire du triangle isocèle, voir Propriétés

Construction du triangle isocèle, voir Constructions élémentaires

Approfondir le triangle isocèle, voir Menu d'en-tête

Types "isocèle"

Selon l'angle au sommet:

S'il est inférieur à 90°, il est acutangle;

S'il est égal à 90°, il est rectangle; et,

S'il est supérieur à 90°, il est obtusangle.

Voir Trapèze isocèle / Découpage en triangles acutangles

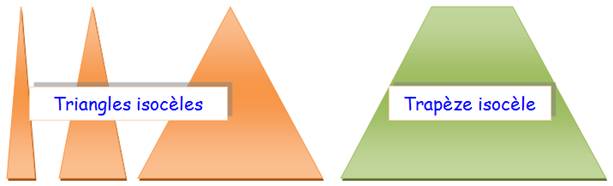
Énigme: combien de triangles isocèles dans le triangle isocèle?

Un triangle isocèle contient quatre triangles isocèles de dimension moitié

ou encore seize pour le quart.

Voir Jeux et énigmes

Jeux – La ROSACE ISOCÈLE

Vous voyez de manière évidente les quatre triangles isocèles colorés en marron. Il en existe d'autres comme AOB. Combien peut-on en trouver sur cette figure? 4, 8, plus …

Solution

TRIANGLE ISOCÈLE

BC est la base du triangle isocèle

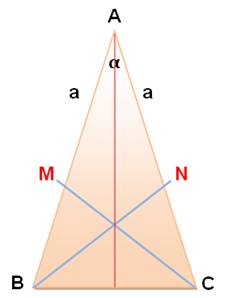
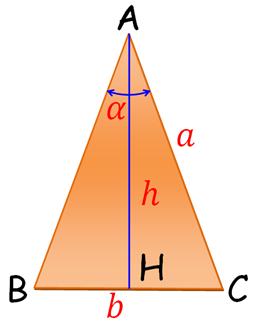
A est le sommet.

L'angle en A (alpha) est l'angle au sommet.

Les angles en B et en C sont égaux.

Aire:

A = 1/2 a² sin

Voir Justification et autre formule

La médiatrice de la base BC
est aussi hauteur, médiane et bissectrice. Elle constitue aussi un axe de symétrie du triangle.

Les droites BN et CM étant les bissectrices dans un triangle; si BN = CM, alors le triangle est isocèle.

Théorème de Steiner-Lehmus

Le triangle isocèle est rectangle si l'angle alpha est un angle droit.

Un triangle qui a deux côtés de même longueur est isocèle.

TRIANGLE ISOCÈLE-RECTANGLE

Le triangle isocèle est rectangle si l'angle au sommet est un angle droit.

Certaines équerres sont en forme de triangle isocèle-rectangle.

Les angles à la base valent 45° chacun.

Deux triangles isocèles-rectangles identiques forment un carré.

Deux triangles isocèles-rectangles tête-bêche forment un quadrilatère dont les diagonales sont perpendiculaires (sommet-droit en commun).

Voir illustration >>>

triangle

Angles de 45°

Voir Exercice d'application / Tangram / Carré max. en triangle unitaire

Problème classique

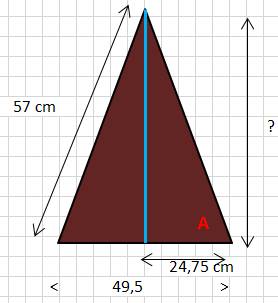
Question

Quelle est la hauteur du triangle isocèle? Je connais les longueurs de la base (49,5 cm) et du côté (57 cm).

Réponse

La hauteur partage le triangle isocèle en deux triangles rectangles.

Le bon vieux Pythagore fera l'affaire.

Je veux aussi connaître l'angle à la base (A).

Là, il faut faire appel à la trigonométrie.

Cos A = 24,75 / 57 = 0,434

A = Arccos (A) = 64,2649°

Sin A = h / 57

Sin 64,2649 = 0,900811

h = 0,900811 x 57 = 51, 3462 cm

Voir Calculs des coordonnées de points d'intersection

Triangle isocèle: si les deux côtés sont égaux, les deux angles aussi – Démonstration

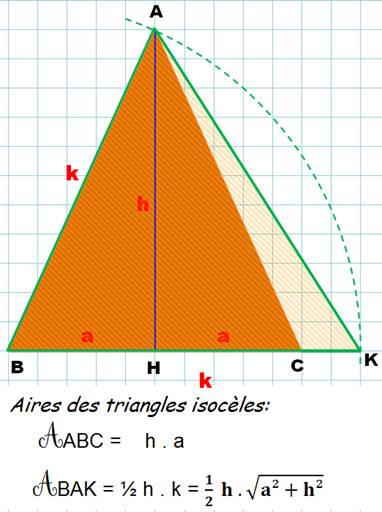
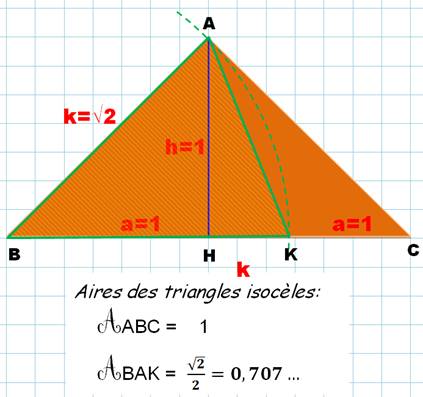
Triangles isocèles en proportions
Triangle isocèle quelconque Un triangle isocèle ABC. On reporte la longueur du côté AB sur le côté BC, qui donne BK. La longueur AB = BK = k est l'hypoténuse du triangle rectangle ABH. Avec le théorème de Pythagore: k² = a² + h² Les deux triangles isocèles ABC et BAK partagent la même hauteur AH = h. Leurs aires sont dans le rapport des bases BC et BK	Voir Aires du triangle et hauteur
Triangle isocèle rectangle et unitaire La même figure que ci-dessus avec a = h = 1. Le triangle AHB est isocèle rectangle. Son aire est moitié de celle du triangle isocèle ABC. Le rapport des aires des triangles isocèles ABC et BAK devient: Remarquez que le rapport entre les aires des deux triangles est un nombre irrationnel (décimales sans fin). On dit que ces aires sont incommensurables (en gros, la division ne tombe pas juste)	Cette figure montre une bonne méthode pour dessiner simplement une aire en racine de 2.

Triangle isocèle dans triangle isocèle

Triangle isocèle SBC avec ses côtés SC et SB mesurant 2a.

Triangle isocèle MBC avec ses côtés valant a.

Ces deux triangles isocèles ont un angle de base commun en B, ils sont semblables.

Et, leur base est égale à la moitié des côtés. Soit pour le petit: BM = a/2.

Ce triangle illustre une découpe possible avec les nombres:

½ , 1 , 1½ et 2.

Voir Construction géométriques des nombres /

Construction du milieu de AB au compas seul

Voir Nombre 0,5

Le plus petit entier

Le plus petit triangle isocèle ayant ses côtés, une hauteur et son aire en nombre entiers et le triangle (5, 5, 6) >>>

Triangle isocèle 30-30-120
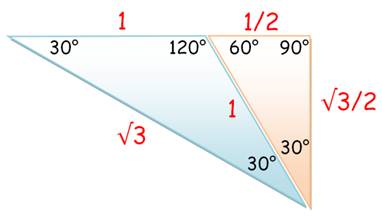
Cette figure illustre une des constructions de racine de 3. Elle est la rencontre: du triangle isocèle 30-30-120, du triangle rectangle 30-60 et de l'hexagone.	Voir Construction de racine de 3
Le petit triangle rose est un triangle rectangle 30-60 dont l'hypoténuse mesure une unité; son petit côté mesure ½ et son grand côté /2. Dans le grand triangle rectangle (bleu + rose): (1 + ½)² + ( / 2)² = 1 + 1 + ¼ + ¾ = 3 = ()²

TRIANGLE D'OR 36-72-72 b = 1 c = PHI
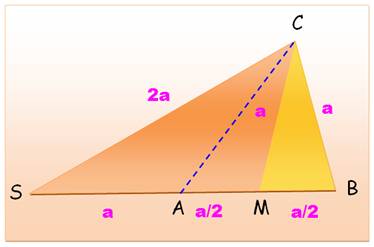
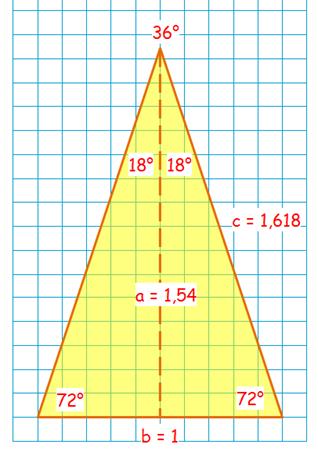
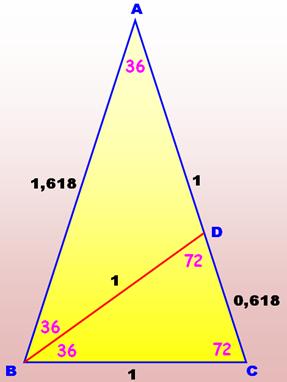
Triangle d'or classique, celui qui constitue les branches de l'étoile à cinq branches. Constitué de deux triangles rectangles 18-72. Le triangle isocèle est tel que sa base mesurant 1, ses côtés égaux mesurent le nombre d'or.	cos = b/2c = 1/1,618 = 0,309 = 72° = 2/5
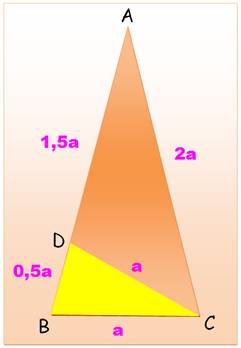
Propriétés de ce triangle d'or La bissectrice BD partage le triangle isocèle en deux autres triangles isocèles ABD et DBC. Angle en C = 72°; Angle en B aussi et sa moitié vaut 36°. Angle en D vaut alors: 180 – 72 – 36 = 72° Le triangle BCD est isocèle et DB = BC = 1; tout comme DAB. Les triangles ABC et BCD sont semblables: angle égal et deux côtés de même longueur. Proportion des côtés: C'est la manière de calculer CD La longueur CD est égale à l'inverse du nombre d'or 0,618 = 1,618 – 1 = 1/ 1,618.	Triangle isocèle avec base = 1 et côtés = nombre d'or. Le tracé de la bissectrice BD produit des propriétés remarquables.

Voir Construction de l'angle de 18° / Construction du pentagone

TRIANGLE D'OR 72-54-54 a = PHI c = 2

Deuxième triangle d'or avec angle de 54° à la base.

La hauteur vaut Phi et les côtés égaux mesurent u nombre entier.

sin = a/c = 1,618 / 2 = 0,809

= 54° = 3/10

Voir Autres valeurs de dimensions (pentagone)

TRIANGLE D'OR a = PHI b = 1

Troisième triangle d'or de hauteur égale au nombre d'or; c'est la base, cette fois, qui mesure un nombre entier.

Trois triangles d'or

Les trois triangles respectent deux mesures:

un côté est entier, et

un autre vaut le nombre d'or.

Chacun d'eux utilise une ligne trigonométrique différente: sinus, cosinus et tangente.

tan = 2a/b = 2 x 1,618 = 3,236

= 72° 82796214…

Aire du triangle isocèle

h = a cos ( / 2)

b/2 = a sin ( / 2)

_AHC = ½ h . b/2 = ¼ h . b

_ABC = 2 _AHC = ½ h . b

= ½ a cos ( / 2) x 2 a sin ( / 2)

= a² sin ( / 2) cos ( / 2)

Or sin(x) cos(y)

= ½ [ sin(x + y) + sin(x – y) ]

Avec x = y = / 2:

sin ( / 2) cos ( / 2)

= ½ [ sin + sin (0) ]

= ½ sin

En reprenant la formule pour l'aire:

_ABC = ½ a² sin

Autre évaluation de l'aire

h² = a² - (b/2)²

= ¼ (4a²- b²)

h = ½ (4a²- b²)^1/2

_ABC = h . b/2

= ¼ b (4a²- b²)^1/2

Cas typiques

Avec le triangle isocèle unité (a = 1).

Degrés	10	20	30	34,36	36
Radians	0,17453293	0,34906585	0,52359878	0,59969513	0,62831853
Sin	0,17364818	0,34202014	0,5	0,56439083	0,58778525
Aire Trg	0,08682409	0,17101007	0,25	0,28219541	0,29389263

Degrés	40	45	50	60	70	80
Radians	0,6981317	0,78539816	0,87266463	1,04719755	1,22173048	1,3962634
Sin	0,64278761	0,70710678	0,76604444	0,8660254	0,93969262	0,98480775
Aire Trg	0,3213938	0,35355339	0,38302222	0,4330127	0,46984631	0,49240388

Degrés	90	120	180	270	360
Radians	1,57079633	2,0943951	3,14159265	4,71238898	6,28318531
Sin	1	0,8660254	0	-1	0
Aire Trg	0,5	0,4330127	0	0	0

Voir Trigonométrie

Isocèle en trigonométrie
Montrez que si cette relation est vérifiée le triangle est isocèle.
Autre écriture
Valeurs trigo.
Angle du triangle (180°).
Angles supplémentaires.
Simplification:
Conclusion:

Pour rapprochement: formule de l'angle double:
Autre considération Loi des sinus
Loi des cosinus
En rapprochant le résultat avec celui de la loi des sinus

Linguistique

Langues

Français triangle isocèle

Anglais isosceles triangle

Espagnol triangulo isosceles

Italien triangolo isoscele

Allemand gleichschenkliges Dreieck

Étymologie

Du grec isoskêles: avec iso, égal et skelos, jambe.
Via le bas latin isosceles.
Pour une fois le français a simplifé en faisant sauter le "c".

Anglais

Prononciation: aɪˌsɒsəliːz ˈtraɪæŋɡ(ə)l quelque chose comme "aille zo cé lis traille angol" (en gras: mettre une intonation plus forte, une accentuation).

An isosceles triangle is a triangle with (at least) two equal sides. This property is equivalent to two angles of the triangle being equal.

An equilateral triangle is a special case of an isosceles triangle having not just two, but all three sides and angles equal. Another special case of an isosceles triangle is the isosceles right triangle.

Problème du billard d'Alhazen

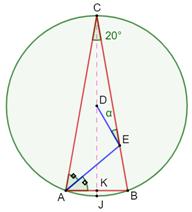
Trouvez un triangle isocèle inscrit dans le cercle tel que les côtés passent par deux points donnés.

Pour un billard circulaire: la balle A doit rebondir une fois et frapper la balle B.

Problème ardu dont la solution date de 1997.

Voir Billard d'Alhazen

Suite

Triangle isocèle rectangle – Exemples

Partage du carré en triangles isocèles

Partage du triangle isocèle en deux parts égales

Résolution du triangle isocèle

Quizz géométrie – Illustration

Tout triangle quelconque est isocèle ?

Triangle – Index

Triangle isocèle – Bissection

Triangle isocèle – Intersections

Triangle isocèle 20 80 80

Triangle isocèle dans le carré

Triangle isocèle dans une feuille A4

Triangle isocèle de 45° au sommet

Triangle isocèle et ovale

Triangles isocèles dans l'énigme du tirebouchon

Triangles isocèles et partage de l'hexagone

Types de triangles

Voir

Allumettes et quatre triangles isocèles

Égalités des triangles

Jeux

Malhorne

Médianes

Platon et sa vision des éléments

Polygones

Probabilité d'obtenir un triangle obtusangle

Quadrupler le triangle

Résolution du triangle quelconque

Symétries

Triangle de Pythagore

Cette page

http://villemin.gerard.free.fr/GeomLAV/Triangle/Types/TrgIsoce.htm

Rosace isocèle: 24 triangles isocèles

Avec AO, nous pouvons former AOB, AOC, AOD, AOE, AOF, AOG et AOH. Soit 7 triangles dont un AOE est réduit à un angle plat. En l'éliminant il reste 6 triangles.

Avec BO, sans revenir sur le point A déjà fait: BOC, BOD, BOE, BOF, BOG et BOH. BOF retiré, il a 5 triangles.

Avec CO: COD, COE, COF, COG et COH. En retirant COG, il a 4 triangles.

Avec DO: DOE, DOF, DOG et DOH. Sans DOH, il ya 3 triangles.

Avec EO: EOF, EOG et EOH. Tous retenus; soit 3 triangles.

Avec FO: FOG et FOH. 2 triangles.

Avec GO: GOH. 1 triangle.

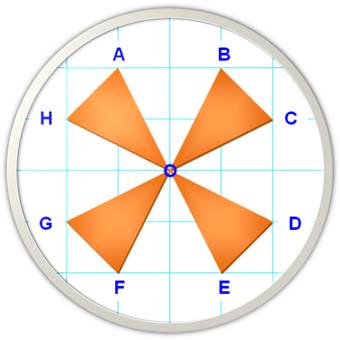
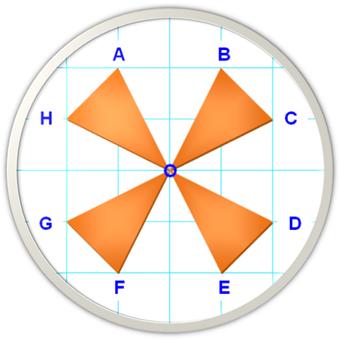
Combien de triangles isocèles dans cette figure en utilisant les sommets de A à H?

Somme: 6 + 5 + 4 + 3 + 3 + 2 + 1 = 24

Attention à un dénombrement trop rapide qui passerait à côté du doublon de 3.

Retour / Dénombrement / Jeux

Cité par Stella Baruk – Dico de mathématiques – Seuil