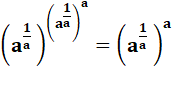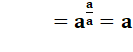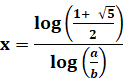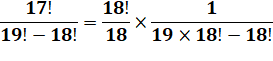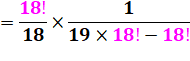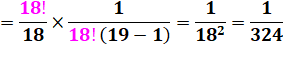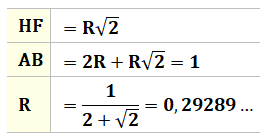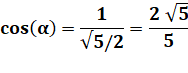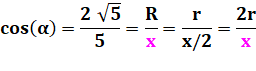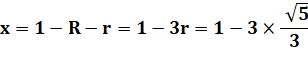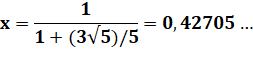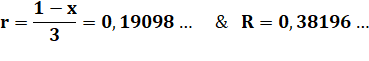Accueil Orientation générale Barre de recherche

DicoNombre DicoMot Math DicoCulture

Atlas des maths Rubriques Index alphabétique

Nouveautés Actualités Références

Édition du: 14/11/2024 M'écrire Brèves de Maths

INDEX Algèbre Énigmes Défis viraux Jeux et énigmes	Problèmes – Défis
	INDEX	50^99 et 99!	Somme de la diagonale
	Divers défis 01	Divers défis 02	Fourmi sur un pavé
	Divers défis 03	Divers défis 04	Coin du carré replié

Divers défis mathématiques Problèmes rencontrés sur le Net proposés comme défis aux Internautes
	Sommaire de cette page >>> Puissances: 3a = 5b = 225 => ab/(a+b) = ? >>> Puissance à étage >>> Équation avec x en exposant >>> Factorielles: 17! / (19! – 18!) = ? >>> Racines carrées: Rac(46 – 12•Rac(14)) = ? >>> Triangle et carré >>> Aire du rectangle ? >>> Deux cercles dans un carré	Débutants Nombres Glossaire Nombres

Puissances: 3a = 5b = 225 => ab/(a+b) = ?	haut
Calcul d'une expression à partir d'une hypothèse. Propriété des exponentielles et des logarithmes: x^y = k => y ln x = ln k On notera aussi que 225 = 15² = 3² x 5² Alors, le calcul se laisse faire …

Voir Factorielles et carrés

Puissance à étage		haut
	En reprenant ce raisonnement avec 5 au lieu de 3, on trouverait x = racine cinquième de 5. D'une manière générale: Vérification

Voir Racine cubique de 3

Équation avec x en exposant		haut
	Notez que le rapport a/b est égal au nombre d'or. Solution générale de:

Factorielles: 17! / (19! – 18!) = ?		haut
Fractions impliquant les factorielles de trois nombres successifs. La soustraction semble poser un problème. L'idée consiste à exprimer les factorielles de 19 et 17 en fonction de la factorielle 18. Celle-ci offre une simplification par 18!

Voir Factorielles et carrés

Racines carrées: Rac(46 – 12·Rac(14)) = ?		haut
Calculer la valeur de cette expression avec racines carrées.
Idée: mettre l'expression sous radical sous la forme d'un carré.
Identité remarquable:	(a – b)² = a² + b² – 2ab
Le produit:
Choix de a et b, par essais et intuition (Intuition de partager la racine de 14 sur a et sur b).
Solution:

Voir Calculs avec radicaux / Calcul impossible avec racines carrées emboitées

Racine carré: Rac(70×71×72×73 + 1)			haut
Calculer la valeur de cette expression avec racines carrées.
Le mieux est de ne pas se limiter à ces valeurs numériques. Nous avons à faire au produit de quatre nombres successifs.		P = n (n + 1) (n + 2) (n + 3) = (n² + n)(n² + 5n + 6) = n^4 + 5n^3 +6n² + n^3 + 5n² + 6n = n^4 + 6n^3 +11n² + 6n
Intuition pour la factorisation en un carré en ajoutant 1.		P + 1 = (n² + an + 1)² = n^4 + 2an^3 + (a²+2)n² + 2an + 1 = n^4 + 6n^3 + 11n² + 6n + 1
On vérifie que a = 3 convient. Le produit de quatre nombres consécutifs plus 1 est un carré.		n (n + 1) (n + 2) (n + 3) + 1 = (n² + 3n + 1)²
Application numérique:
Pour info s'agissant du carré d'un nombre impair.

Voir Brève 841

Triangle équilatéral et carré		haut
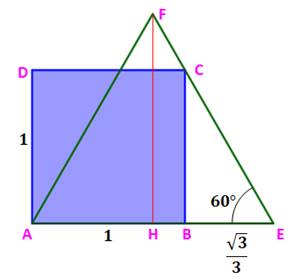
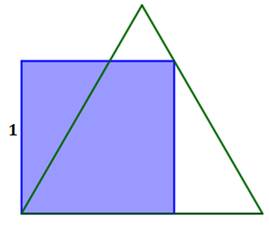
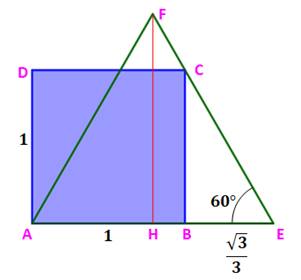
Problème Un carré de côté unité. Un triangle équilatéral disposé comme sur la figure. Quelle est l'aire de ce triangle ? Solution Les angles du triangle équilatéral valent 60° et leur tangente racine de 3.

Aire du rectangle avec ce demi-cercle ?		haut
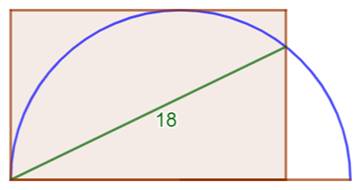
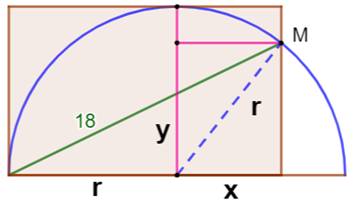
Problème Un demi-cercle. Une corde de 18 cm. Un rectangle construit à partir de cette corde. Quelle est son aire ? Solution Le point M sur le cercle à pour coordonnées x et y. Le rayon du cercle est r. Théorème de Pythagore: x² + y² = r² (r + x)² + y² = 18² r² + 2rx + x² + y² = 18² r² + 2rx + r² = 18² 2r² + 2rx = (2 x 9)² = 2 x 2 x 81 r² + rx = 2 x 81 = 162 Aire du rectangle = aire du carré de cotés r + aire du rectangle de côtés r et x = r² + rx = 162

Proposé par Science & Vie en 2022

Deux cercles dans un carré		haut
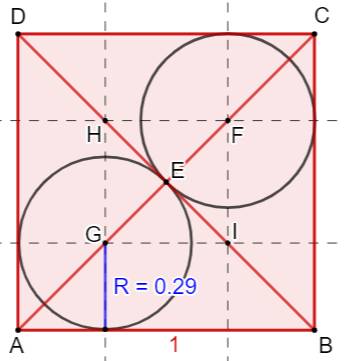
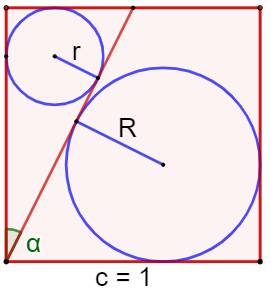
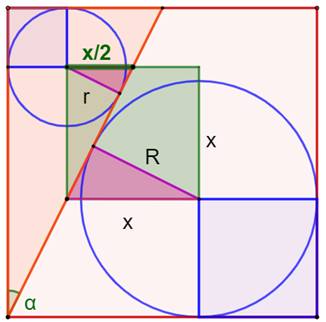
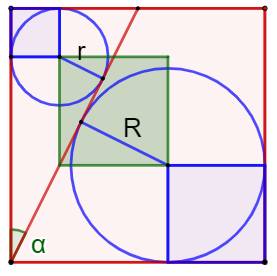
Construction Un carré unité (c = 1) et une "semi-diagonale" joignant un sommet au milieu du côté opposé. Cercles inscrits dans les deux régions du carré. Rapport entre les rayons r et R de ce cercles ? Triangle rectangle Côtés: 1 et 1/2. Hypoténuse: h² = 1² + 1/2² = 5/4 Petit angle alpha (qui vaut 26,56°) Carré vert Construire les carrés bleus de côté r et R. Puis, le rectangle (vert) de sommets les centres des cercles. Ce rectangle est un carré car chaque côté mesure: x = 1 – r – R. La semi-diagonale du grand carré est aussi une semi-diagonale pour ce nouveau carré. Elle coupe le côté du petit carré en son milieu. Triangles rectangles semblables (Figure du bas) Les trois triangles rectangles colorés sont semblables: · même angle alpha, et · deux côtés parallèles ou alignés. Soit les rapports On en déduit Valeurs numériques

Voir Pi dans le carré et deux cercles / Théorème de Pythagore / Théorème de Thalès / Brève 914

Haut de page

Retour	· Algèbre – Index · Énigmes – Index · Brèves – Index
Suite	· Deux cercles dans un carré – Divers défis · Pi dans le carré et deux cercles · Divers défis 02 · Équation en x^4 · Technique de base de l'algèbre · Tracas classiques en algèbre
Voir	· Équations · Calculs avec radicaux
Cette page	http://villemin.gerard.free.fr/aExercic/Probleme/Defis01.htm