NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 02/04/2017 Orientation générale  DicoMot Math Atlas Références M'écrire Barre de recherche DicoCulture Index alphabétique
	TRIANGLES
Débutants Triangle	Types de TRIANGLES						Glossaire Triangle
INDEX Triangle Géométrie	Types	Quelconque		Rectangle	Isocèle	Équilatéral
	Obtusangle	Homologique		Calabi	Reuleaux	Sphérique
			Sommaire de cette page >>> Triangle sphérique >>> Angles >>> Excès sphérique et aire du triangle sphérique

TRIANGLE SPHÉRIQUE
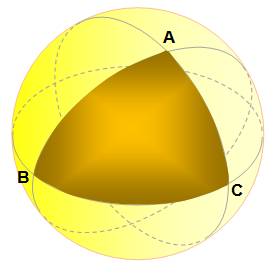
Une sphère et son centre O. Rappel: un grand cercle de la sphère est un cercle de centre O; son plan divise la sphère en deux hémisphères. Deux points divisent le grand cercle en deux arcs. Sauf si ces points sont diamétralement opposés, il y a un petit arc dit arc mineur du grand cercle. Trois points sur celle-ci (A, B et C) Trois grands cercles passant par ces points, deux à deux. Les arcs de cercle entre les points A, B et C sont les côtés du triangle sphérique.

ANGLES du triangle sphérique
L'angle en A est défini par l'angle que font les plans des grands cercles et même chose pour les deux autres. On peut aussi imaginer l'angle entre les tangentes au point aux deux grands cercles. La somme des angles, contrairement au triangle dans le plan, n'est que rarement égale à 180°. - Cas où les trois plans des grands cercles sont perpendiculaires: la somme des angles vaut 3 x 90 = 270°. Équivalent du triangle équilatéral en géométrie sphérique, avec un angle de 90° au lieu de 60. 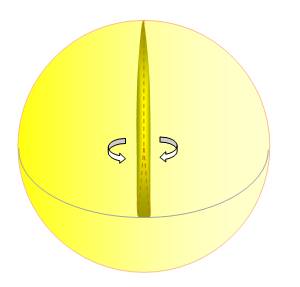- Cas du triangle d'aire minimum tendant vers zéro. Imaginer les deux plans verticaux de la figure précédentes; on ferme l'angle de 90° pour aller jusqu'au maximum 0°. Par contre ces deux plans font toujours un angle de 90° avec le troisième plan. Au total: 0 + 2 x 90 = 180° . 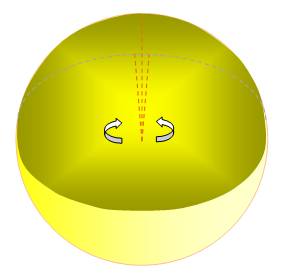- Cas où le triangle sphérique occupe toute une demi-sphère. Imaginer les deux plans verticaux de la figure du haut; on ouvre l'angle de 90° pour aller jusqu'au maximum 360°. Ces deux plans font toujours un angle de 90° avec le troisième plan Au total: 360 + 2 x 90 = 540° . Bilan Dans un triangle sphérique la somme des angles varie de 180° à 540°.	Trois grands cercles perpendiculaires entre eux la somme des angles vaut 270°. 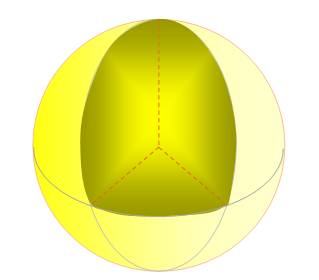Triangle sphérique d'aire nulle: la somme des angles vaut 180°. Deux grands cercles confondus et perpendiculaires au troisième: la somme des angles vaut 540°.

EXCÈS SPHÉRIQUE et AIRE du triangle sphérique
Les trois angles sont mesurés en radians; l'excès sphérique E est une quantité positive. Si R est le rayon de la sphère, l'aire du triangle s'exprime simplement avec l'excès sphérique.	Excès sphérique Aire du triangle sphérique Théorème de Girard (1595-1632)

Retour	Types de triangles Triangle de Reuleaux
Voir	Allumettes Angle Carrés Cercles Cuboctaèdre Droite Égalités des triangles Hexagone Hexagramme, étoile de David Jeux Polygones Probabilité d'obtenir un triangle obtusangle Quadrupler le triangle Résolution du triangle quelconque Symétries Triangle de Pythagore Types de triangles
Cette page	http://villemin.gerard.free.fr/GeomLAV/Triangle/Types/Spheriqu.htm