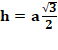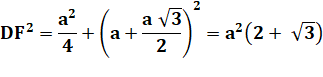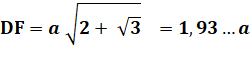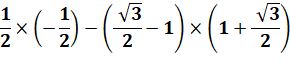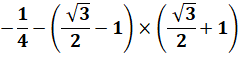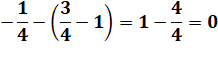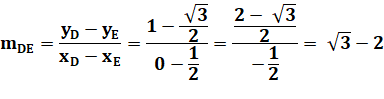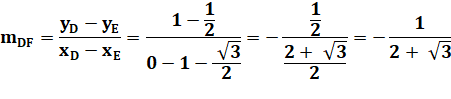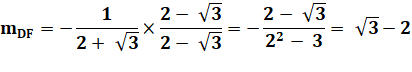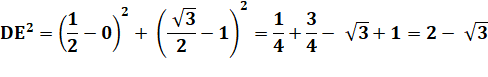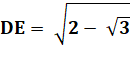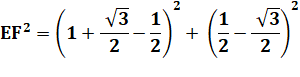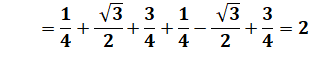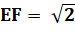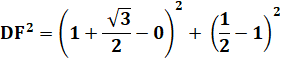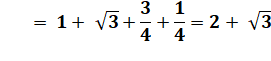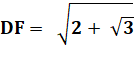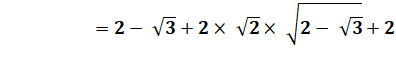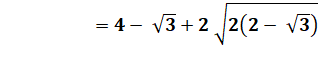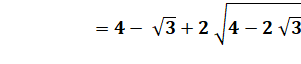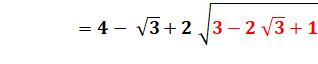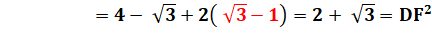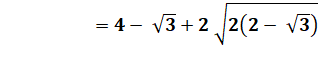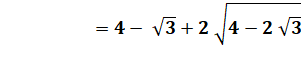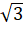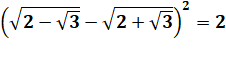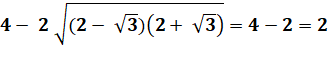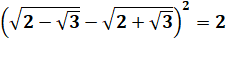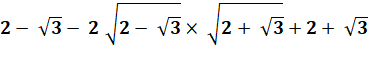|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
et des deux triangles équilatéraux Problème du pentagone non-régulier Une figure simple et de nombreuses
possibilités de démonstrations de niveau cinquième jusqu'à niveau seconde. |
|
|
||
|
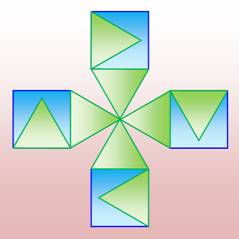
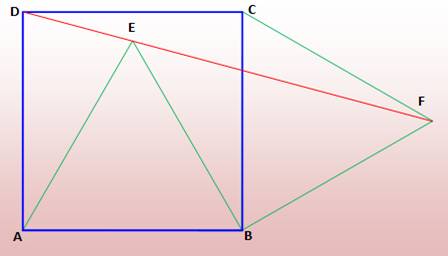
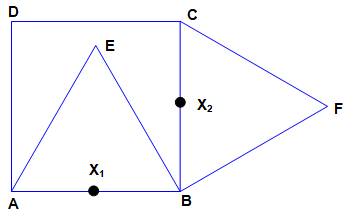
Construction Un carré
ABCD et deux triangles équilatéraux
AEB et BFC. Montrez que les points D, E
et F sont alignés. Donnez la mesure du segment
DF. |
|
|
|
Remarque express pour matheux |
Un rotation de + 60° du triangle BCF autour de B amène EF en AC soit √2 fois
le côté du carré: EF = a√2 |
|
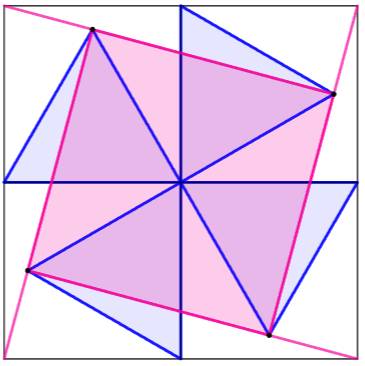
Figure
complétée
Le quadrilatère rose formé
au centre est un carré
![]()
Niveau cinquième
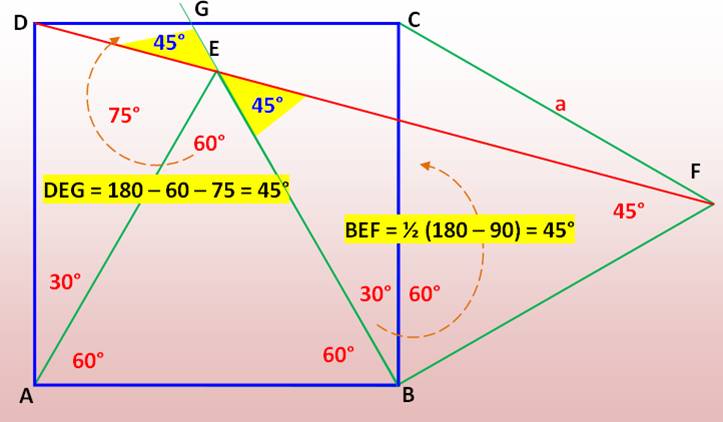
Une idée pour suivre la démonstration sur la
figure: copiez-la avec l'outil de capture d'écran.
|
|
||
|
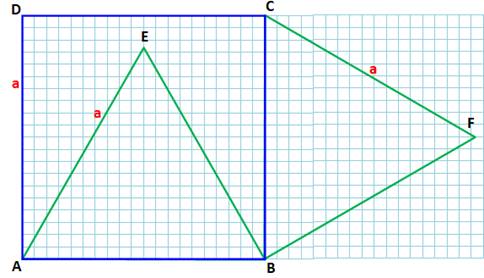
Hypothèses |
ABCD est un carré de côté a. AEB et BFC sont des triangles équilatéraux de côté a. |
|
|
Théorèmes |
La somme des angles dans un triangle quelconque
est égale à 180° >>> Dans un triangle
isocèle, les deux angles adjacents à la base sont égaux et valent
chacun: ½ (180° - angle au sommet) >>> |
|
|
Solution
1 DÊF est un angle plat |
DÊF = DÊA + AÊB + BÊF |
|
Évaluation
de DÊA dans le triangle isocèle
DAE |
Angle en A = 90 – 60 = 30° Angle en D et en E = ½ (180 –
30) = 75° |
|
Évaluation
de BÊF dans le triangle isocèle
EBF |
ABE = 60° ; EBC = 30° ; CBF =
60° => EBF est
droit BEF = ½ (180 – 90) = 45° |
|
Reprise
de notre angle DÊF |
DÊF = 75 + 60 + 45 = 180° = Angle plat Les points D, E et F sont alignés. |
|
Triangle
isocèle CDF |
Angle au sommet = 90 + 60 = 150° Angle à la base = ½ (180 – 150) = 15° |
|
Triangle
isocèle DAE |
Angle au sommet = 90 – 60 = 30° Angle à la base = ½ (180 – 30) = 75° Angle CDE = 90 – 75 = 15° |
|
Égalité
des angles |
CDF = CDE = 15° Les points D, E et F sont alignés |
|
Mesure
de DF |
DF² = F'D² + FF'² F'D = a/2 FF' = a + hauteur du triangle équilatéral |
|
Évaluation |
|
|
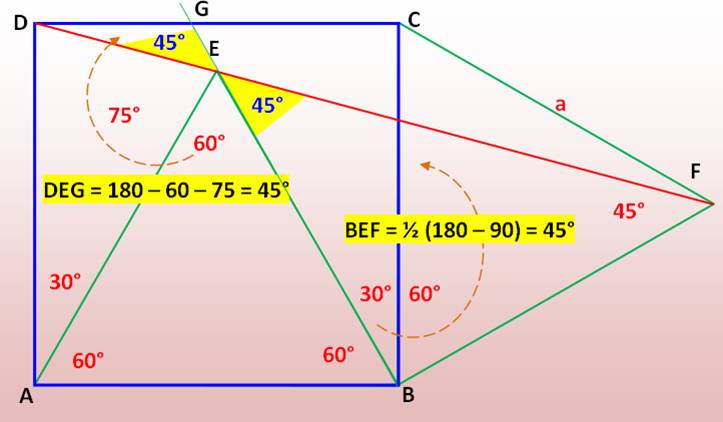
Solution
2 – Autour du point E On prolonge BE qui coupe DC
en G. Les angles DEG et BEF sont égaux (Voir
la figure). Or B, E et G sont aligné; alors, D, E et F le sont.
|
|
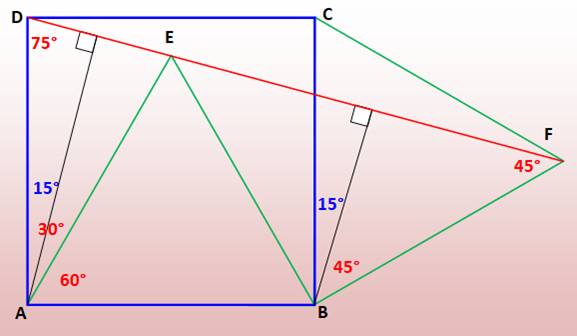
Solution
3– Hauteurs de triangles qui sont parallèles On trace la hauteur issue de
A du triangle DAE. Son angle par rapport a AD est égal à 15° (Voir figure). On trace la hauteur issue
de B du triangle EBF. Son angle par rapport a AD est égal à 15° (Voir figure). Ces deux hauteurs font le
même angle par rapport à deux droites parallèles (AD et BC), elles sont
parallèles. Étant perpendiculaires aux segments DE et EF, ceux-ci sont parallèles.
Ayant un point commun (E), ils sont alignés.
|
![]()
Niveau
seconde
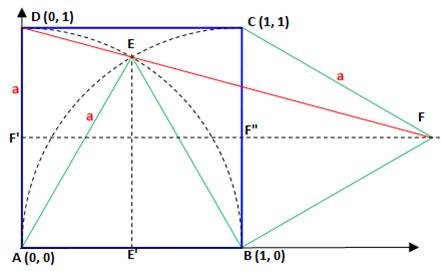
|
Utilisation des coordonnées des vecteurs |
|
|
|
On
choisit A comme origine du système
d'axes. Ce qui fixe naturellement les coordonnées des quatre sommets du
carré. |
A (0, 0) B (1, 0) C (1, 1) D (0,1) |
|
|
Coordonnées
des sommets E et F des triangles
équilatéraux. On calcule la longueur de la hauteur du triangle équilatéral avec le théorème
de Pythagore. |
|
|
|
Vecteurs
DE et DF |
|
|
|
Deux
vecteurs sont
colinéaires si le déterminant est nul Utilisation
d'une identité
remarquable (a² - b²). Le
déterminant est nul, les vecteurs DE et DF sont colinéaires. |
|
|
|
Solution analytique (2) Utilisation de l'équation des droites |
|
|
|
Les
coordonnées sont connues |
Voir
ci-dessus |
|
|
Coefficient
directeur de la droite DE |
D (0,1)
|
|
|
Coefficient
directeur de la droite DF Multiplication
par
le conjugué pour chasser le radical du dénominateur |
D (0,1)
|
|
|
Les
coefficients directeurs des deux droites sont égaux (elles ont la même
pente). |
Les droites issues du même point D sont
confondues Les points D, E et F sont alignés. |
|
|
|
||
|
Rappel
des coordonnées |
D (0, 1)
|
|
|
Longueur
de DE |
|
|
|
Longueur
de EF |
|
|
|
Longueur
de DF |
|
|
|
Comparaison Il est
plus facile de rester avec les carrés du fait de la présence de radicaux. Pensez à
reformer un carré sous le radical lorsque c'est possible comme ici.. |
DF = DE + EF ? DF² = (DE + EF)² ?
|
|
|
|
||
|
Loi
des cosinus (formules d'al Kashi)
|
|
|
|
Triangle
DCF Angle en
F = 90 + 60 = 150 ° cos 150°
= - |
|
|
|
Triangle
DAE Angle en
A = 30 cos 30° =
|
|
|
|
Triangle
EBF isocèle et rectangle Angle en
B = 90° |
EF² = EB² + FB² = 1² + 1² = 2 |
|
|
Comparaison Plus
facile avec les carrés en mettant tout les radicaux "compliqués" du
même côté. |
DE + EF = DF ? Si égalité, alors alignement.
|
|
|
|
||
|
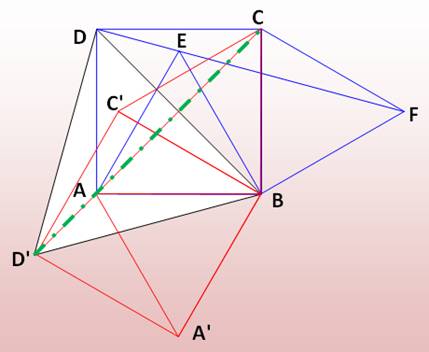
La figure d'origine en bleu est dupliquée (rouge)
et on lui applique une rotation
de 60° autour de B. Image de F = C Image de E = A Image de D = D' Montrer que F, E et D sont alignés, c'est montrer que C, A et D' sont
alignés. Le triangle DBD' est équilatéral car BD = BD'
(diagonale du carré) et l'angle en B est égal à 60° (somme de trois angles,
facile à identifier). D'C est un des axes de symétrie de ce
triangle, donc médiatrice
de DB. Or AC, diagonale du carré, est aussi médiatrice de DB. Alors, C, A et
D' sont bien alignés. |
|
|
|
|
||
|
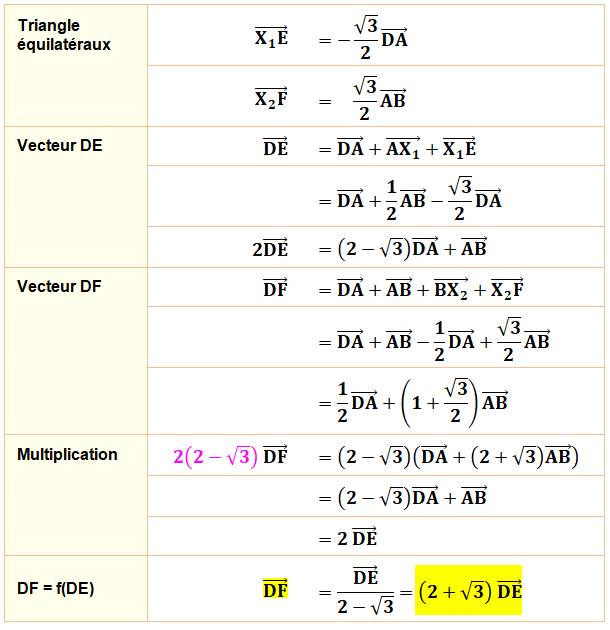
Une solution élégante qui montre la puissance du calcul
vectoriel. La relation établie en fin de calcul montre que
les vecteurs DE et DF sont parallèles et, étant issus du même point D, ils
sont alignés. Les points D, E et F sont alignés. Solution
proposée par Maxime
Maillard |
|
|
|
Note: 2 + √3 = 3,73205080… |
||
![]()
|
|
||
|
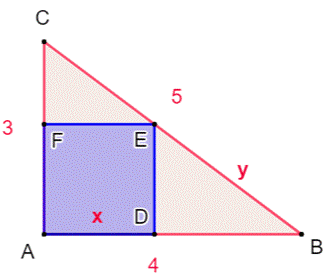
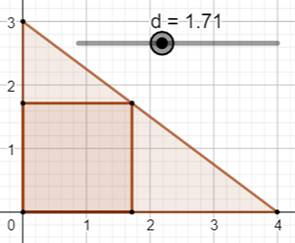
Construction Un triangle rectangle (par exemple: 3, 4, 5). Quelle est la taille maximale du carré construit
? Avec GeoGebra,
on construit le triangle ABC. Le curseur d est mis en place. Le carré ADEF (bleu) est construit avec un côté égal
à d. Le curseur est ajusté pour placer le sommet E sur
le côté BC On lit 1,71 sur le curseur. La taille maximale du
carré est 1,71… Piste On note que les triangles rectangles CBA, CFE et
EDB sont semblables. On utilisera le théorème de
Thalès qui précise les proportions. Calculs avec les triangles CFE et
CAB
|
|
|
Voir Brève
52-1035 / Suite de carrés dans le triangle rectangle
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Site |
|
|
Cette page |
http://villemin.gerard.free.fr/GeomLAV/Triangle/Exercice/TriaEq01.htm
|
![]()