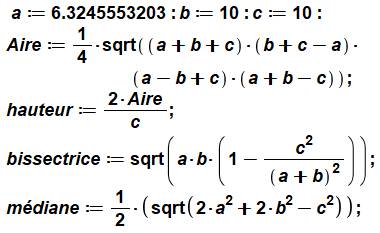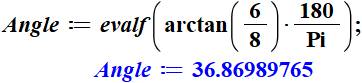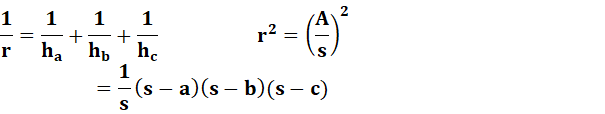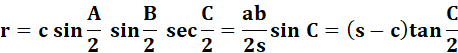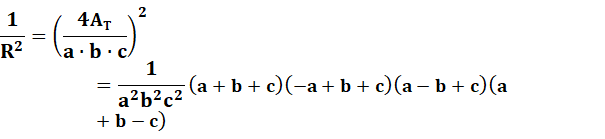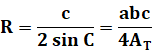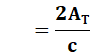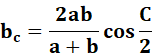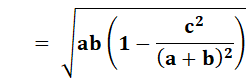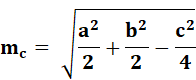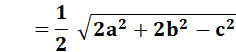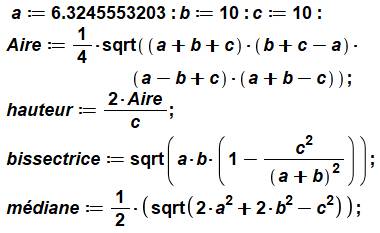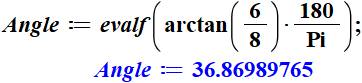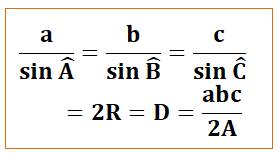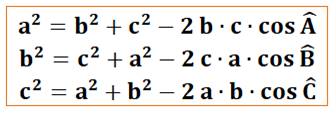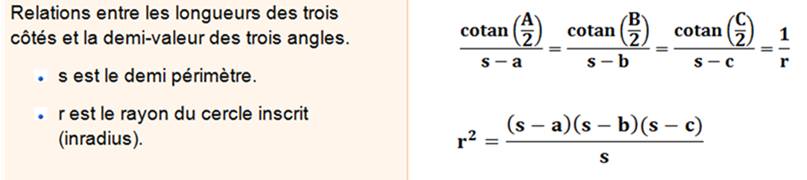NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 20/12/2024 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	TRIANGLES
Débutants Triangle	Résolution							Glossaire Triangle
INDEX Résolution Triangle	Résolution	Trois côtés (LLL)			Deux côtés (LAL)		Un côté (ALA)
	Formules	Trois angles (AAA)			Deux côtés (LLA)		Un côté (AAL)
	Formules avancées		T 13 14 15			Hypoténuse
	Sommaire de cette page >>> Figure & notations >>> Angles et côtés >>> Aire du triangle >>> Cercles >>> Droites >>> Loi des sinus >>> Loi des cosinus			>>> Loi des projections >>> Loi des demi-angles >>> Loi de Napier >>> Loi des tangentes >>> Loi des cotangentes >>> Formule de Mollweide >>> Médianes >>> Exemple de Résolution

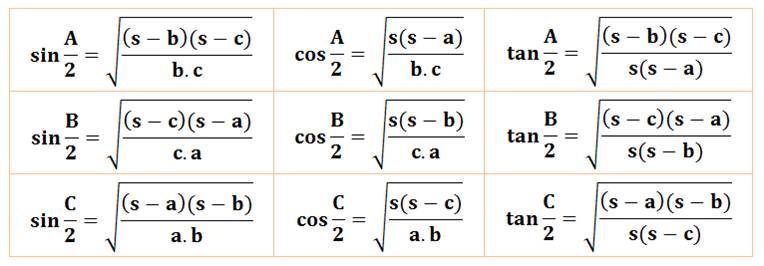
Formules fondamentales pour la RÉSOLUTION

du TRIANGLE QUELCONQUE

Toutes les formules utiles pour résoudre les triangles (connaissant trois mesures, trouver les trois autres).

Voir Relations trigonométriques – Formulaire pour le triangle

FIGURE & NOTATIONS

A B C	Sommets
a, b, c	Longueur des côtés
ha	hauteur portant sur le côté a
R	Rayon du cercle circonscrit (Oc)
r	Rayon du cercle inscrit (OI)
2s s	= a + b + c (périmètre) = demi-périmètre
AT	= Aire du triangle

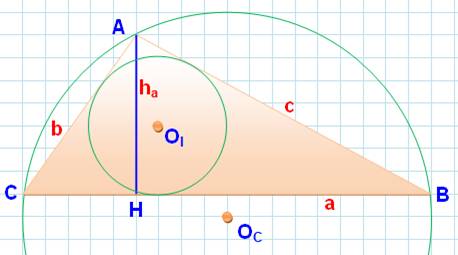
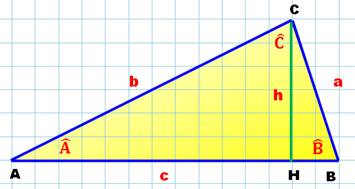
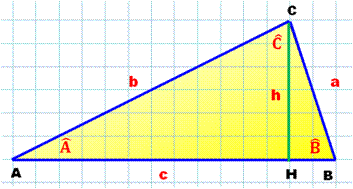
Le triangle est quelconque

(même s'il apparait rectangle sur cette figure; CB n'est pas un diamètre du cercle circonscrit).

Merci à Sylvie Gaudel pour ses remarques

Angles et côtés

a = b cos C + c cos B b = a cos C + c cos A c = b cos A + a cos B

Ici et pour la suite, le chapeau, symbole des angles, est omis.

AIRE DU TRIANGLE
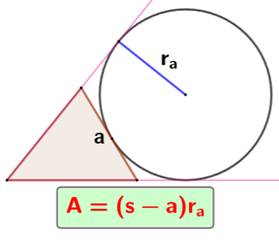
AT est donnée par l'une de ces formules (s = demi-périmètre): Avec une cévienne quelconque / Avec le rayon d'un cercle exinscrit Voir Démonstration / Relations avec la hauteur / Formules de Héron / Application de la formule du sinus / Autre application Triangles héroniens / Calcul de l'aire des quadrilatères

Voir Application dans le calcul d'un invariant 2 dans le triangle quelconque

CERCLES
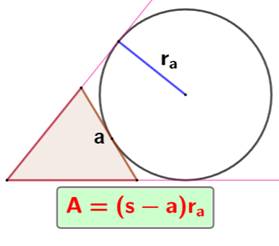
Rayon du cercle inscrit Voir Démonstration Rayon du cercle circonscrit Voir Démonstration

Droites
Hauteur Bissectrice Médiane Note: calcul de l'aire et de la hauteur avec les formules pour l'exercice. On lit évidemment ces valeurs directement sur la figure: A = 6 x 10/2 = 30 et ordonnée de C = 6.	Exemple Calculs numériques

LOI des SINUS
Avec D = 2R le diamètre du cercle circonscrit et A l'aire du triangle.

SUITE Démonstrations et applications

Voir Application au partage du cercle / hauteur du sommet

LOI des COSINUS (formules d'Al Kashi)

SUITE Démonstrations et applications

Voir Exemple de calcul / Calcul de l'aire des quadrilatères / Al Kashi / Triangle rectangle ?

LOI des PROJECTIONS

LOI des DEMI-ANGLES

LOI de NAPIER

LOI des tangentes

Voir Formules trigonométriques d'addition

LOI des cotangentes

Formules de Mollweide

Médianes
Longueur des médianes avec milieu sur les côtés a, b et c.

Triangle quelconque rationnel

Comment trouver les fractions exactes qui caractérisent les longueurs et les angles dans un triangle quelconque >>>

Suite	Formules avancées dans le triangle quelconque Relations trigonométriques – Formulaire Résolution du triangle LLL (trois côtés connus) Formule de Héron et sa démonstration Aire de la projection des triangles Quadrilatère et diagonale inconnue
Voir	Cercle Géométrie Polygone Triangle - Index Triangle – Introduction Triangle rationnel Trigonométrie
Cette page	http://villemin.gerard.free.fr/GeomLAV/Triangle/Calcul/RelQuel.htm