triangle et son quadruple

NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 03/07/2021 Orientation générale DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	TRIANGLES
Débutants Triangle	Propriétés – Curiosités				Glossaire Triangle
INDEX Types de triangles Triangle	Point Milieu	Droites et points	Pappus	Point et triangles
	Angles (180°)	Quantité de triangles	Torricelli	Triangles et triangles
		Quatre triangles	Heilbron	Carrés triangles
		Représentation	Brocard	Cercles et triangles
		Sommaire de cette page >>> Triangle rectangle >>> Triangle quelconque >>> Triangle médian >>> Triangle antimédian

Triangle MÉDIAN

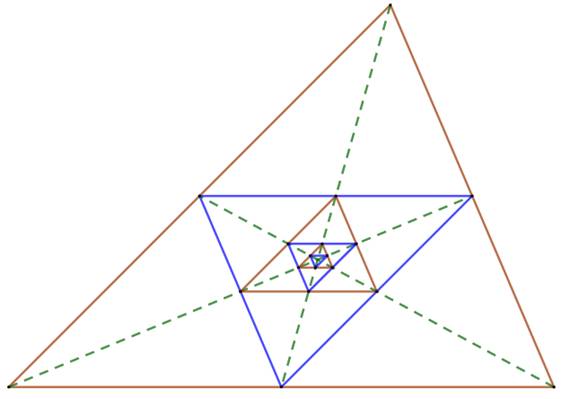
Idées – Multiplication par quatre

Tracez un triangle dont l'aire est quadruple d'un autre.

Les hauteurs de l'un sont les médiatrices de l'autre (démonstration du point de concours unique).

L'un est le triangle médian de l'autre.

TRIANGLE RECTANGLE

Pour quadrupler le triangle rectangle, il suffit d'en ajouter trois autres disposés comme indiqué sur la figure.

Remarquons que:

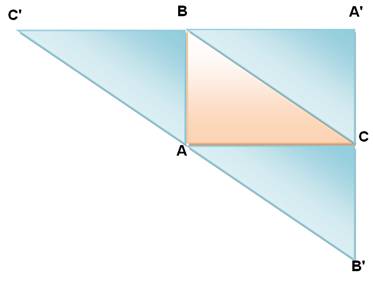
AB = CA' = B'C

BC = C'A = AB'

AC = BA' = C'B

Une collection de parallélogrammes (dont l'un est rectangle).

Remarquons encore que

AB est une des hauteurs du triangle ABC tout en étant une médiatrice du triangle A'B'C'.

TRIANGLE QUELCONQUE

Pour quadrupler un triangle quelconque, on peut procéder comme pour le triangle rectangle en ajoutant trois autres triangles égaux au premier.

Ce qui revient au même, nous dessinons la parallèle à chaque côté passant par le côté opposé.

Du fait de la création de parallélogrammes, nous retrouvons les mêmes égalités que précédemment

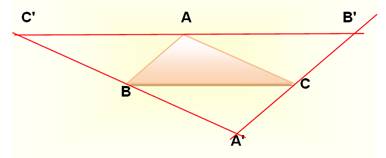
AB = A'C = CB'

BC = C'A = AB'

AC = BA' = C'B

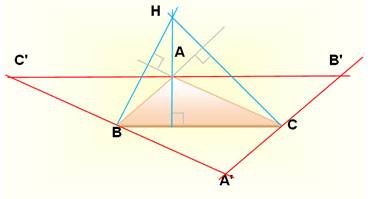
Construisons les hauteurs du triangle ABC

AH, BH et CH

Ce sont aussi les médiatrices du triangle A'B'C' (perpendiculaire au côté en son milieu).

Les hauteurs de l'un des triangles sont les médiatrices de l'autre.

Triangle médian
Les sommets du triangle médian sont les points milieux du triangle d'origine. The triangle formed by joining the midpoints of the sides of a given triangle is called the medial triangle.
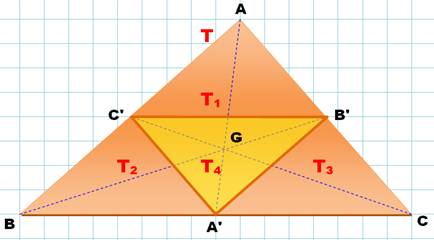
En termes d'aires:		T₁ = T₂ = T₃ = T₄ = T/4
La réunion de deux triangles forme des parallélogrammes.		T₁ + T₄; T₂ + T₄; T₃ + T₄
Les médianes de T sont aussi les médianes de T₄.		G est le centre de gravité de T et de T₄
Les hauteurs de T₄ sont les médiatrices de T.		Le centre O du cercle ciconscrit de T est aussi l'orthocentre de T₄.
Les triangles médians successifs ont tous les mêmes médianes Leur aire est égale à 1/4 du triangle mère. Ils sont homothétiques et un sur deux dans le sens direct.
Anglais	Three medians of a triangle meet at a point – centroid of the triangle. The medians of a triangle serve as the medians of its medial triangle.

Triangle antimédian ou anticomplémentaire
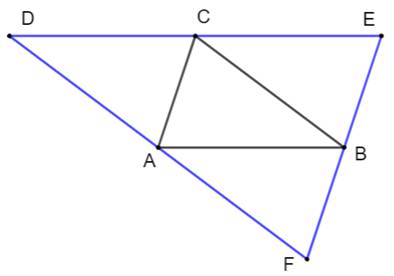
Les rôles sont renversés. DE // AB; EF // AC et DF // BC Le triangle DEF est l'antimédian de ABC ou ABC est le triangle médian de DEF. Les points D, e et f sont les points exmédians.
Coordonnées trilinéaires des points exmédians	x' = - 1/a : 1/b : 1/c y' = 1/a : - 1/b : 1/c z' = 1/a : 1/b : - 1/c

Voir

Cette page