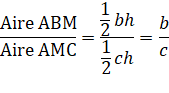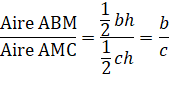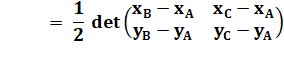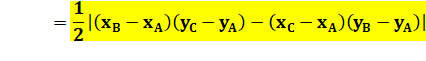![]()
|
|
Ce site est désormais accessible en http://diconombre.fr/index.html et
pour cette page voir le lien en fin de page |
|
22 Novembre 2025
![]()
|
||||||||||||||||||||||||||||||||
![]()
|
TRIANGLES QUELCONQUES Quelles
sont leurs propriétés: les propriétés générales communes à tous les triangles
? Comment
calculer l'aire de ces triangles? |
Anglais:
arbitrary triangle

Source image
: https://www.emaze.com
|
Définition
du triangle quelconque &
du triangle scalène |
|
|
Voir Types de
triangles
Le qualificatif quelconque est surtout utilisé pour
introduire une hypothèse dans un énoncé: soit un
triangle quelconque. On pourrait tout aussi bien dire: soit un triangle. En anglais: let ABC be any triangle. Le plus souvent, l'emploi du qualificatif "quelconque"
vise à exclure des égalités sur les côtés ou des valeurs remarquables sur les
angles, comme l'angle droit. Formellement la notion de triangle quelconque
englobe toutes sortes de triangles. Cependant, cette précision avertit qu'il
ne faut pas compter sur une propriété particulière pour conduire une
démonstration sur ce triangle. Toute précision complémentaire sur le triangle
lui retire son statut de quelconque. Le triangle scalène est proche du triangle
quelconque avec cependant une nuance: cet adjectif a été introduit pour
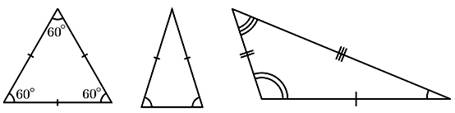
distinguer les triangles selon la longueur des côtés:
Équilatéral Isocèle Scalène NB.
les angles du triangle scalène sont
également différents, mais il n'est pas interdit que l'un d'eux soit droit. Auquel cas, le triangle est rectangle non-isocèle. Anglais: A
scalene triangle is a triangle that has no congruent sides. With a right angle, it is a right scalene triangle.
Si la longueur des côtés est un nombre entier, le triangle est un triangle entier. S'il est rectangle, il s'agit d'un triangle de
Pythagore. Si de surcroit, l'aire est un nombre
entier, le triangle est héronien. |
|
Merci à Raphaël L.G. pour ses
remarques pertinentes
|
|
|
|
Voir Construction
du triangle quelconque Générales
Voir Les trois
géométries
Soit
trois longueurs, elles ne constituent un triangle que si l'une d'entre elles
est plus grande que la somme des deux autres. La
différence des longueurs de deux côtés est toujours plus petite que la
longueur du troisième côté. Conséquence de la propriété précédente:
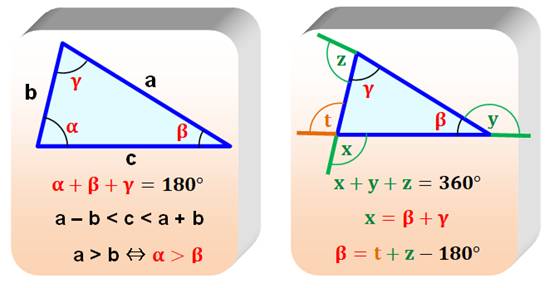
Résumé des propriétés des angles et des côtés
Voir Brève 54-1079 Particulières
Avancée
27
(a² + b² – c²)² (b² + c² – a²)² (c² + a² – b²)² |
|
|
|
||
|
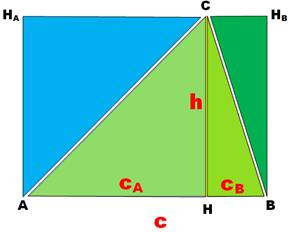
Calcul de l'aire Aire du
rectangle AHCHA = h . cA Aire du
rectangle BHCHB = h . cB Aire du
rectangle ABHBHA = h . c Aire du triangle
ABC = ½ h . c |
L'aire du triangle est égale à la moitié de celle du rectangle. |
|
|
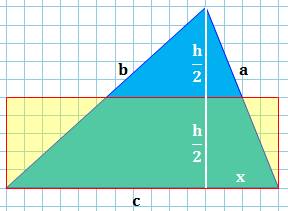
Alternative Couper la hauteur
en deux moitiés et dessiner le rectangle. La tête bleue du triangle se loge
dans les deux triangles jaunes. D'où la formule de l'aire: A = c x (h/2) |
|
|
|
En fonction des trois côtés (Méthode d'Al-Khwarizmi en 820) Dans les deux
triangles rectangles définis par la hauteur et avec le théorème de Pythagore. |
h² = b² – (c – x)² = b² – c² + 2cx –x² h² = a² – x² b² – c² + 2cx = a² x = (a² – b² + c²) / 2c |
|
|
Triangle (13, 15, 14) En reprenant les
formules ci-dessus. Le plus petit triangle acutangle avec une aire
rationnelle. Connus des Grecs, des Hindous et des Arabes. Même
source ou alors découvertes séparées? |
x = (13² – 15² + 14²) /
(2x14) = 140 / 28 = 5 h² = 13² – 5² = 144 h = 12 A = ½ x 12 x 14 = 84 Voir Résolution
complète |
|
Voir Toutes les
formules de calcul de l'aire du triangle /
Relations de Héron pour le calcul de l'aire en
connaissant les côtés /
Coordonnées barycentriques dans le
triangle
|
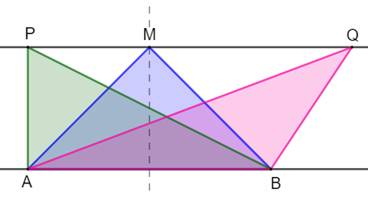
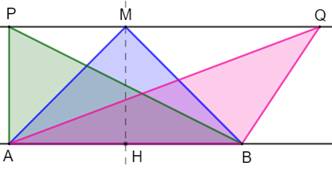
Deux droites parallèles. Un segment AB formant la base de trois triangles ayant
M, P et Q pour sommets. Quel est le triangle qui a la plus grande aire et celui qui a le plus petit périmètre ? |
|
|
|
||
|
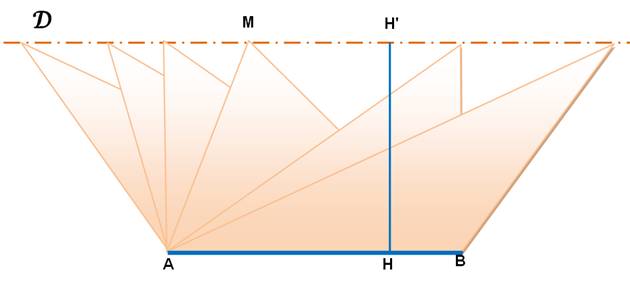
Tous les triangles de cette figure
ont la même aire: AB x
HH' / 2. Un côté commun et un sommet sur une
parallèle à ce côté commun. |
||
|
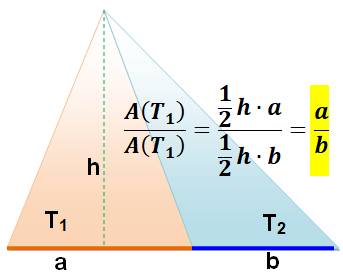
Deux triangles de même sommet et de base alignées;
le rapport de leur aire est égal au rapport des longueurs de leur base. |
|
|
Voir
Démonstration du théorème de Thalès / Rapport des aires dans le triangle isocèle /
Problème
du triangle dans quatre carrés / Défi des cinq triangles dans
le triangle / Trisection
du quadrilatère
|
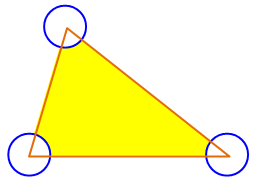
Énigme Comment
calculer l'aire de la partie jaune par rapport à celle du triangle ? Les
cercles sont identiques, le triangle est queconque.
|
Solution Les
trois secteurs colorés,
assemblés, forment un angle de 180° (somme des angles du
triangle).
Les
trois secteurs non-jaunes du triangle forment un demi-cercle dont l'aire vaut
L'aire
de la partie jaune est égale à celle du triangle diminuée de celle du
demi-cercle. |
|
|
||
|
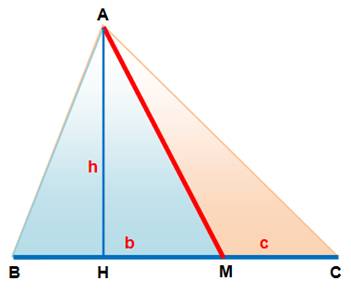
Calculons l'aire du triangle ABM et du
triangle AMC. Aire ABM = ½
bh Aire AMC = ½
ch Comparons ces deux aires
|
|
|
|
Une sécante
dans un triangle quelconque partage le triangle en deux parties d'aires
proportionnelles aux longueurs des segments découpés sur le côté. Si b = c, la sécante
est la médiane et
cette médiane partage le triangle en deux triangles de même aire. |
||
Voir Parallélogramme 123
|
|
||
|
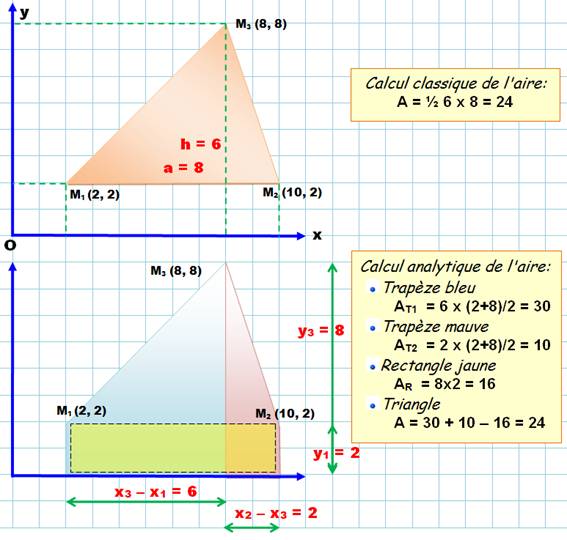
Dessinons le
triangle sur un système d'axes qui permet de fixer les coordonnées des trois
sommets.
L'aire du
triangle se calcule facilement en calculant l'aire des deux trapèzes (bleu et
mauve) en déduisant l'aire du rectangle (jaune). Dans le cas
général (base non parallèle à l'axe x), le rectangle devient lui aussi un
trapèze) |
|
|
|
Rappel: aire du trapèze |
Produit
de la hauteur par la demi-somme des bases. >>> |
|
|
Formulation analytique de l'aire du
triangle |
|
|
|
Application numérique |
|
|
Voir Calcul analytique de l'aire du
quadrilatère quelconque
Aire du triangle avec coordonnées des sommets (calcul général)
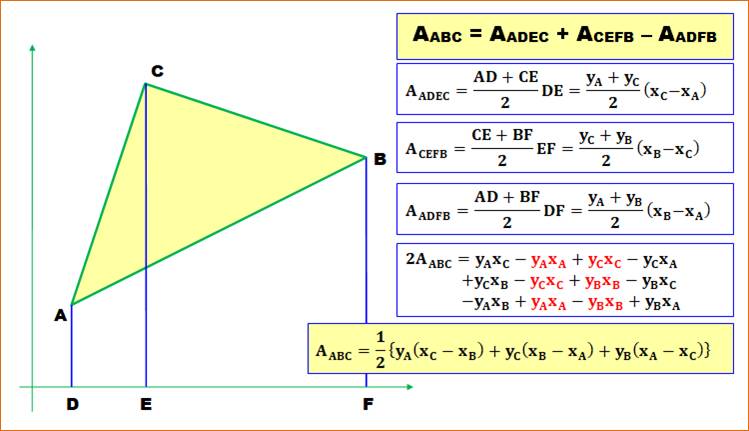
Voir Aire du trapèze / Exercice sur l'aire du triangle
/ Exemple avec équation des
droites
|
|
||
|
Triangle ABC |
|
|
|
Aire du triangle
ABC = valeur absolue du déterminant
développé (jaune), aussi appelé produit mixte. |
|
|
|
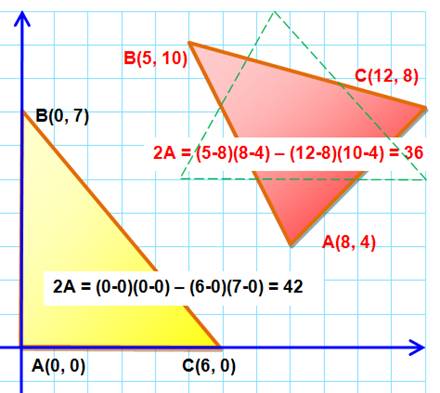
Exemples Triangle jaune: Aire = 42/ 2 = 21; Valeur vérifiable car le triangle est rectangle:
½ (6 x 7) = 21. Triangle rouge: Aire = 36 / 2 = 18; Valeur vérifiable graphiquement. Le triangle vert est égal au rouge à une
rotation près. Aire du triangle vert: 7,2 x 5 = 18. |
|
|
Voir démonstration en Aire du parallélogramme
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
On pose: |
p = 1/2 (a + b + c) k² = p ( p – a
)( p – b )( p – c ) Ma
= 1/2 ( b² + c² ) – 1/4 a² |
||||||||||||||||||||||||||||||||||||||||||||||||||
*FH Voir Formule d'Héron |
|||||||||||||||||||||||||||||||||||||||||||||||||||
Voir Toutes les
relations pour la résolution du triangle quelconque
Exemple: Aire avec le rayon du cercle inscrit
|
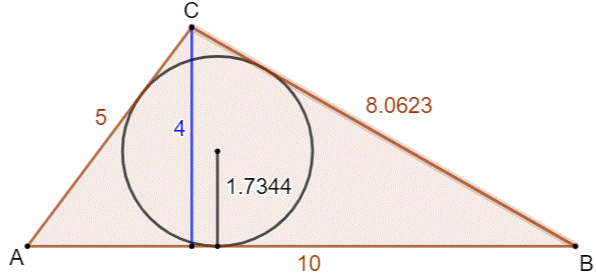
Avec le cercle inscrit Demi-périmètre
= (10 + 5 + 8,0623) /2 = 11,53115 Aire du
triangle = 11,53115 × 1,7344 = 19,999 …
Classique avec la hauteur Aire du
triangle = ½ 10 × 4 = 20 Notez que,
du fait de 5 et 4, le pied
de la hauteur coupe AB en 3 et 7. |
Voir Démonstration
de la formule / Brève 48-941
|
|
|
|
Les triangles dont les mesures des côtés et de l'aire sont entières ou rationnelles sont dits héroniens. Voir
Triangles héroniens Lorsque de tels triangles sont rectangles, ils donnent lieu à des développements considérables avec la notion de nombres congruents. |
|
Bien
gondolé, ce quelconque!

|
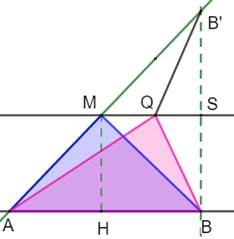
Question Deux droites parallèles. Un segment AB formant la base de trois triangles ayant
M, P et Q pour sommets. Quel est le triangle qui a la plus grande aire et celui qui a le plus petit périmètre ? Aire (A) Tous les triangles avec base AB et un sommet quelconque
sur la droite PQ ont la même aire: A = ½ AB × MH. Périmètre (P) C'est le triangle isocèle AMB qui a le plus petit périmètre.
En effet: Dessiner le point B' symétrique de B par rapport à la
parallèle MQ. MS est la médiatrice de BB' Périmètres: Or,
dans le triangle AQB': AB' < AQ + QB' Lorsque le point Q se rapproche de M, le périmètre
diminue. Il est minimum lorsque Q = M; le triangle est alors isocèle. |
Aire APB = Aire AMB
= aire AQB = AB x MH / 2
AB' < AQ + QB' Le triangle isocèle
a le plus petit périmètre. |
Retour
/ Autres
énigmes / Brève 574
Merci à
Dan B. et Philippe S. pour leurs remarques pertinentes
![]()
|
Suite |
|
|
Voir |
|
|
Cette page |
![]()