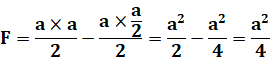Triangle isocèle, approche pour débutant

Le triangle isocèle est l'un des premiers objets géométriques abordés par les enfants en primaire. C'est l'occasion d'introduire des notions et du vocabulaire qui serviront pour la suite au collège.

En effet, pour beaucoup d'élèves, même doués de facilités, la géométrie passe pour être une matière rébarbatives qui nécessite d'apprendre énormément de définitions.

Jeux
Un escalier en briques lego avec autant de marches pour monter d'un côté et pour descendre de l'autre. En construisant cet escalier nous réalisons un triangle isocèle. Posé sur un côté (sa base), les deux autres côtés ont la même longueur. Coupé en deux (trait bleu), c'est la même chose de chaque côté, comme vu dans un miroir. Construite avec plus de briques, plus basse ou plus haute, plus large ou moins large, ce sera toujours un triangle isocèle.	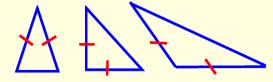La construction dessine un triangle isocèle. Une forme identique des deux côtés.
Je bricole! Une planche et une tige métallique plantée verticalement. Deux clous espacés de la même distance par rapport à la tige. Une ficelle est tendue entre les deux clous tout en reposant sur le haut de la tige en fer. Peu importe la distance entre les clous (ici: 2 x 3 = 6 cm) ou la hauteur de la tige (ici: 4 cm), le triangle formé est un triangle isocèle. La longueur des deux cordes sont égales (ici: 5 cm). Remarquez que la tige coupe le triangle isocèle en deux parties identiques: deux triangles rectangles égaux.	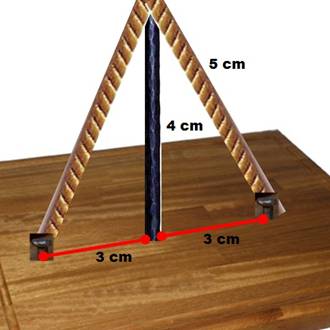La tige en fer est à angle droit avec la base (rouge), c'est la hauteur du triangle isocèle.

Construction
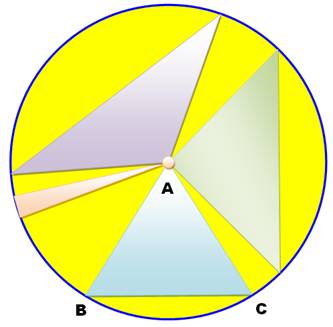
Méthode 1, par le sommet À partir d'un point A, dessinez un cercle de rayon quelconque R. Choisissez deux points sur le cercle (B et C). Le triangle ABC est isocèle. Ses côtés AB et AC ont pour longueur le rayon du cercle. AB = AC = R Les exemples de la figure sont tous les quatre des triangles isocèles.
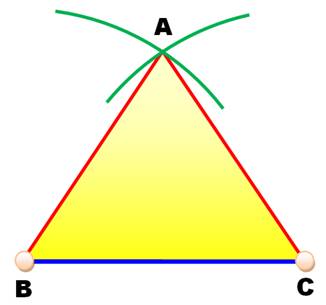
Méthode 2, par la base À partir d'un segment BC, dessinez deux arcs de cercle de même rayon R. Ils se coupent en A. Le triangle ABC est isocèle. AB = AC = R Quelle que soit la longueur du rayon R, le triangle reste isocèle (R doit être supérieur à la moitié de BC; sinon les cercles ne se coupent pas).

Merci à Joseph Paoli pour sa contribution

Voir Toutes les constructions élémentaires

Le triangle isocèle
L'anatomie du triangle isocèle. Il a: trois côtés: AB, BC et CA; trois sommets A, B et C. Le segment CH qui forme un angle droit avec la base AB est appelé la hauteur principale du triangle isocèle. Les deux triangles rectangles AHC et BHC sont égaux: les cotés AC et BC sont égaux (ils ont la même longueur); Les segments AH et BH sont égaux les angles en A et en B sont égaux les deux angles en C son égaux (angle ACH et angle BCH) On verra que CH est une hauteur qui est à la fois bissectrice de l'ange C et médiatrice du segment AB.	Périmètre du triangle isocèle: P = a + 2c = 2 (b + c)
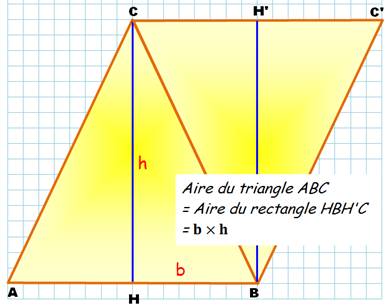
La hauteur (bleue) partage le triangle isocèle en deux triangles rectangles identiques. En ajoutant le même triangle isocèle comme indiqué sur l'illustration, on remarque que le rectangle HBH'C couvre une surface égale à celle du triangle isocèle. ou encore égale à deux triangles rectangles. La surface (ou plus exactement: l'aire) du rectangle est donc égale à: A = b x h = ½ a x h.	En disposant de cette manière deux triangles isocèles identiques, on forme quatre triangles rectangles identiques.

Angles à la base

Les angles à la base du triangle isocèle sont égaux et aigus (plus petits que 90°). En effet, la somme des angles dans un triangle quelconque est 180°. Lorsque l'angle au sommet est proche de 0°, les deux de la base se partagent moins de 180°, soit moins de 90° pour chacun.

Si l'angle au sommet vaut 60°, les deux autres valent: 180 – 60 = 120°, et chacun d'eux vaut: 120 / 2 = 60°. Les trois angles sont égaux, le triangle est équilatéral.

Si l'angle au sommet vaut 90°, c'est un triangle isocèle rectangle. Les angles à la base valent: (180 – 90) / 2 = 45°.

Devinette

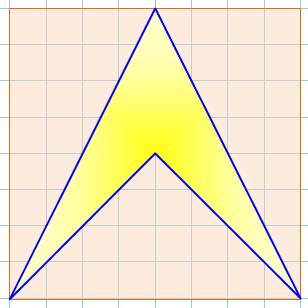
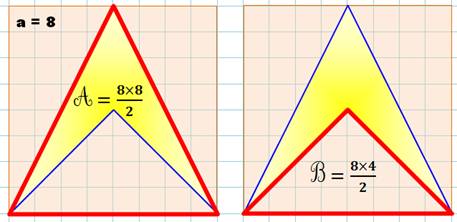
Aire de la flèche?

Solution

La magie du triangle isocèle
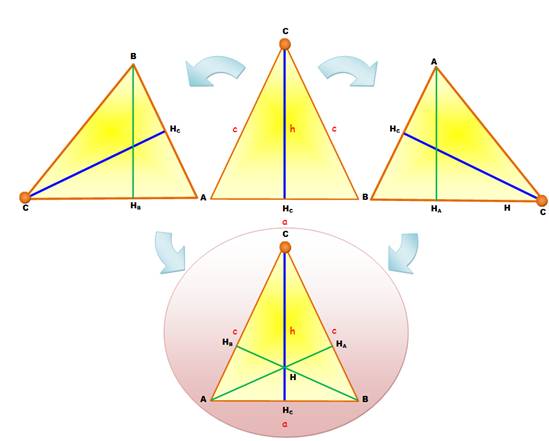
Le triangle initial "debout" sur sa base avec sa hauteur principale (bleue). On le bascule à droite et aussi à gauche Pour chacun, on dessine la hauteur, la droite qui passe par le sommet et qui est à angle droit avec le côté opposé (vert). Finalement, les trois figures sont superposées. Incroyable, les trois hauteurs se croisent au même endroit (H)	Dans un triangle isocèle, et c'est vrai pour tout triangle, les trois hauteurs de rencontrent au même point. Les trois hauteurs sont concourantes.
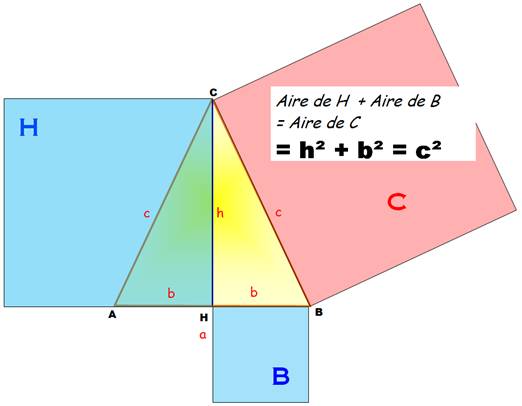
On construit les carrés H, B et C sur les côtés du triangle rectangle. L'aire de chaque carré est égale au carré de la longueur de leur côté. Alors, sur la figure, il y a autant de rose que les deux bleus réunis. Cette relation de Pythagore est importante car elle permet de calculer la longueur du troisième côté lorsqu'on connait la mesure des deux autres. Exemple: si b = 3 et h = 4, alors c² = 3² + 4² = 9 + 16 = 25 et c = 5.	C'est Pythagore qui a popularisé cette propriété: la surface des carrés bleus est égale à celle du carré rose.

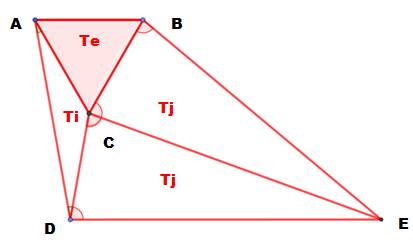
Une composition de triangles isocèles
Problème Sur cette figure: trois triangles isocèles: Ti et les deux Tj, plus un triangle équilatéral (ABC). De plus AB et DE sont parallèles. Quelle est la valeur du petit angle en A (Angle CAD) ?
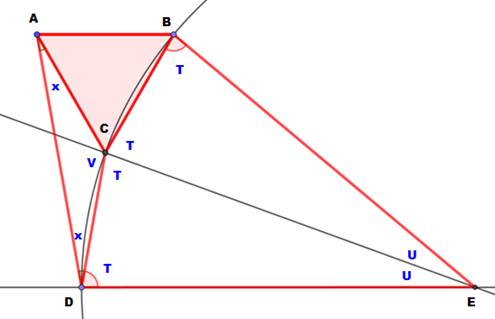
Construction avec Géogebra: AB de longueur donnée. ABC triangle équilatéral. CD de même longueur que AB. CE bissectrice de ACD. Cercle passant par B, C et D. E milieu du diamètre issu de C. Parallèle en D à AB Ajustez la figure (en pointant le point D) pour que le point E soit sur cette parallèle. La mesure de l'angle x est 20° et celle de l'angle T, 80°. Note: Avec cette figure x = 60 – T. C'est la contrainte de parallélisme qui ancre la valeur de s à 20°.
Calcul En exploitant les 360° autour du point C. Puis les angles en E et en D, en tenant compte des parallèles AB et DE.	2x = 180 – V 2x = 180 – (360 – 60 – 2T) = 2T – 120 T = x + 60 x + 60 = 180 – x – T 2x = 120 – T = 120 – x – 60 3x = 60 x = 20° et T = 80°