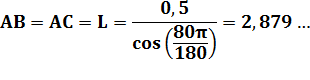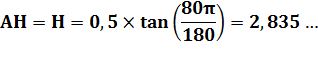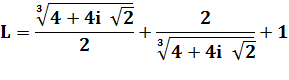|
|||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
TRIANGLE ISOCÈLE 20°, 80°, 80° Triangle isocèle particulier qui fait l'objet de calcul d'angles. Exemples
de problèmes où une construction est nécessaire pour d'aboutir à la solution.
Comment la trouver, intuition mathématique ou logique? Il est vrai que la
construction faite, la résolution est plus facile. |
|
|
||
|
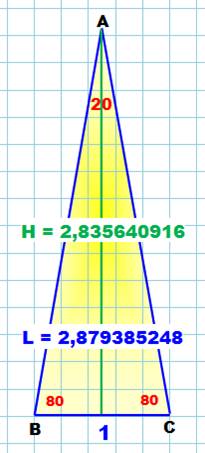
Triangle
isocèle avec une base de longueur BC = 1 Longueur des
côtés
Longueur des
hauteurs
Périmètres et
aire
|
|
|
|
Pour
information Le nombre
L est solution de l'équation x3 – 3x2 + 1 = 0 |
|
|
Voir Résolution du triangle isocèle
|
|
||
|
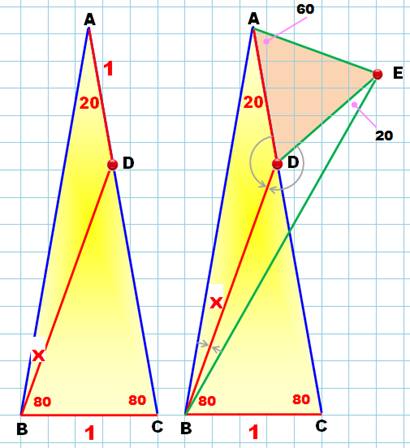
Problème Un
triangle 20 80 80. La longueur de la base BC est reportée en AD. Quelle est la valeur de l'angle x
= ABD? Idée Construire
un autre triangle identique au premier qui va doubler la valeur de x. Solution En A on
dessine la base du nouveau triangle: AE = BC = AD et angle en A = 80°. En
comparant les triangles ABC et BAE, ils ont
Le
triangle ADE est équilatéral avec un angle de 60° et deux côtés de même
longueur. L'angle DEB vaut 80 – 60 = 20°. Dans les triangles
ADB et EDB, les angles en
D sont égaux, de même que les angles en A et E (20°); les troisièmes angles
sont égaux, soit 2x = 20°. Soit la valeur de x = 10°. |
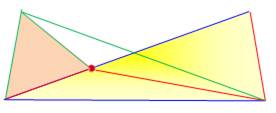
Le créateur de ce problème avait
sans doute la figure de droite au départ et il l'a dépouillée pour créer
cette énigme.
Deux traiangles isocèles siamois
(un côté commun). |
|
Célèbre problème réputé difficile
|
Le problème qui suit daterait
d'au moins de 1916. Posé lors d'un examen d'entrée au collège Peter and
Sidney Sussex College, Cambridge University. Il est réapparut dans la revue Mathematical Gazette en 1923. Divers mathématiciens ont
relevé le défi et ont trouvé diverses solutions géométriques ou
trigonométriques. Voir références Je présente une solution
qui est basée sur la recherche de symétrie. |
|
|
|||
|
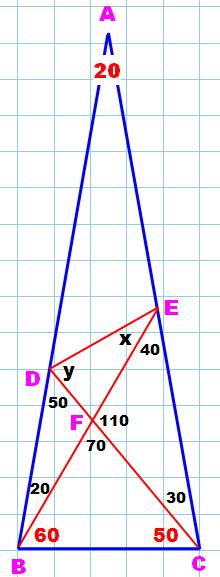
Problème Sur la
base BC, construisons un triangle particulier BFC dont les angles valent 60° et 50°. Les côtés
prolongés coupent AB et AC en D et E, créant un nouveau triangle DEF. Trouvez
la valeur des angles x et y. Réflexions –
Recherche de pistes de raisonnement Les
angles à la base valent 80°. L'angle DBE = 20°, comme l'angle au sommet. Le triangle
AEB est isocèle. Un indice pour la solution ? La
connaissance des angles à la base, permettent de propager les valeurs des
angles dans la figure (valeurs en noir). Malheureusement, sans possibilité de
conclure sur x et y, sinon que x + y =
110° L'énoncé
nous fait construire un angle de 60°, valeur propice à faire naitre un triangle équilatéral. Une piste? Comme souvent en géométrie, la solution nécessite
la construction de relais pour atteindre le but. La piste du triangle
équilatéral suggère de symétriser la figurer en superposant sur cette figure
sa figure symétrique. Alors, il sera possible de remonter les angles
jusqu'à atteindre x et y. |
Une variante existe avec les
angles 60° et 70° au lieu de 60° et 50°. |
||
|
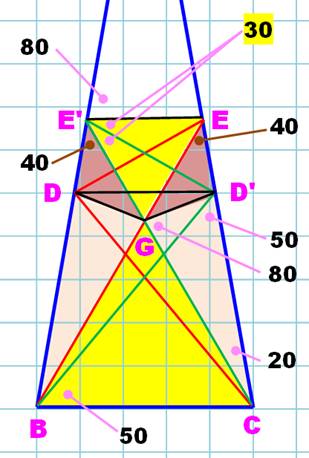
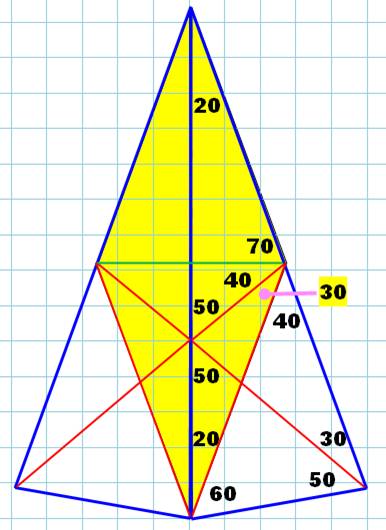
Solution Telle que
dessinée la figure fait apparaitre deux triangles équilatéraux (jaunes) et
deux couples de triangles isocèles (ocres). Le
triangle BCD' est isocèle (angles: 50° et 80° par
construction => 50° pour le troisième). Le
triangle BGC est équilatéral (deux angles à 60°,
par construction). BC = CG = CD' Le
triangle GCD' est isocèle. Angle au sommet 20°
=> angles à base = 80°. Triangle GD'E: son angle en E vaut 180 – 60 – 80 = 40°; son angle
en G vaut 180 – 60 – 80 = 40° => il est isocèle. Le
quadrilatère ED'GE', formé d'un triangle
équilatéral adjacent à un triangle isocèle est un cerf-volant. La droite
passant par E'D' est un axe de symétrie qui coupe
l'angle en E en deux parties égales. Or,
l'angle en E' vaut 180 – 40 – 80 = 60° L'angle x
vaut 30° et y = 180 – 70 – 30 = 80°. |
En construisant la figure
demandée (rouge) et sa symétrique (verte), la solution devient pratiquement
évidente, en tout cas à l'œil. |
||
|
Solution
"presque" muette Elle consiste
à dupliquer la figure pour faire apparaitre des symétries. Une
simple remontée des valeurs des angles permet de trouver la valeur cherchée. Note
personnelle Il me semble que cette solution est la plus
simple. De plus, c'est celle qui vient à l'esprit généralement en premier
tout autant que celle présentée ci-dessus, à peine plus laborieuse. |
|
||
|
|
||
|
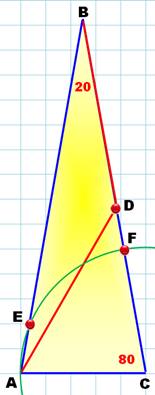
Problème Triangle isocèle
ABC avec angle en B = 20°. Segments:
DA = DB. Cercle de
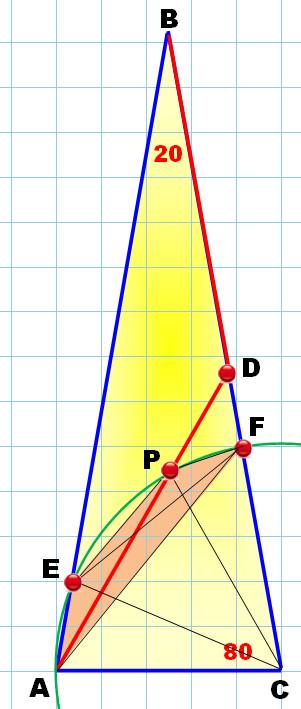
centre C et de rayon CA. Démontrez que AE = DF Idée Comme
nous l'avons vu, nous allons essayez de trouver des symétries pour remonter
de AE vers DF (Figure du bas). La
construction du quadrilatère AEPF semble une bonne
piste. A vue d'œil, c'est un trapèze
isocèle. Pourvu que le triangle PDF soit isocèle et aurons gagné. Résolution
|
Données
Construction
|
|
![]()
|
Suite |
|
|
Voir |
|
|
|
|
|
Cette page |
http://villemin.gerard.free.fr/GeomLAV/Triangle/Types/TrgIsoce.htm |
![]()